5.1.1 平行四边形的边、角性质 课件 鲁教版数学八年级上册

这是一份5.1.1 平行四边形的边、角性质 课件 鲁教版数学八年级上册，共42页。

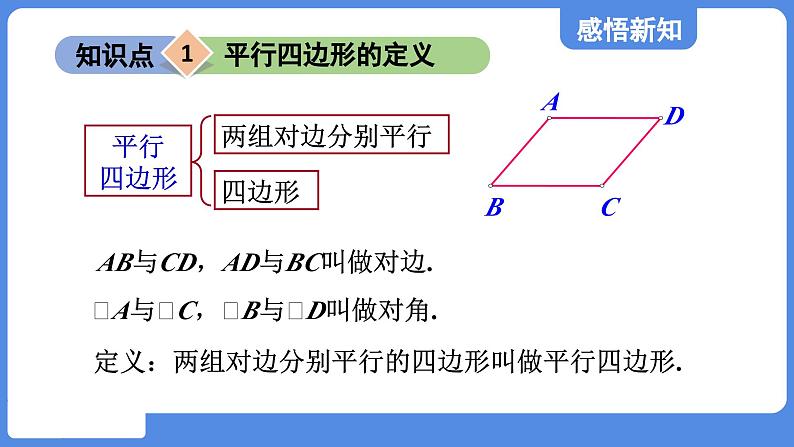
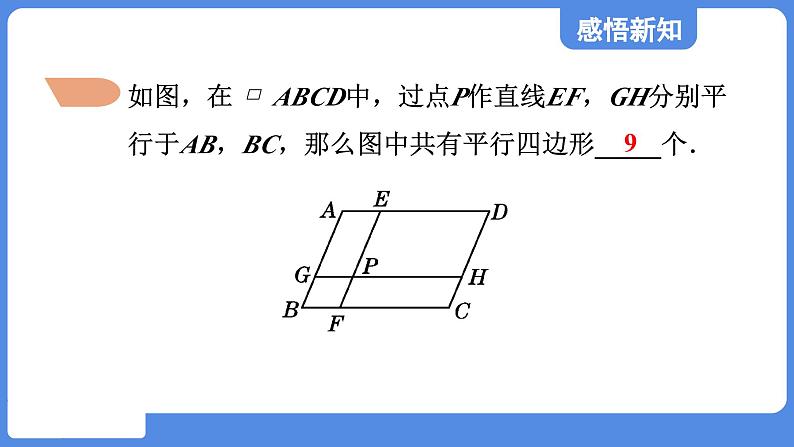
第5章 平行四边形5.1 平行四边形的性质第1课时 平行四边形的边、角性质平行四边形的定义平行四边形的对称性平行四边形的对边的性质平行四边形角的性质回顾与思考两组对边分别平行四边形平行 四边形∠A与∠C，∠B与∠D叫做对角.AB与CD，AD与BC叫做对边.定义：两组对边分别平行的四边形叫做平行四边形.知识点平行四边形的定义11.平行四边形的定义有两个要素：(1) 是四边形；(2)两组对边分别平行.作为四边形，平行四边形具有一般四边形的一切性质，如有四条边，四个内角，两条对角线，内角和为360°，外角和为360°等.作为平行四边形，它区别于其他一般四边形的特殊性质为：平行四边形的两组对边分别平行.2.平行四边形的定义既是它的一个性质，又是它的一种判定方法：∵四边形ABCD是平行四边形，∴AB ∥ CD，AD ∥ BC；反过来，∵AB ∥ CD，AD ∥ BC，∴四边形ABCD是平行四边形.例1如图，在 ABCD中，过点P作直线EF，GH分别平行于AB，BC，那么图中共有平行四边形_____个．9根据平行四边形的定义，知AB∥CD，AD∥BC，由已知可知，EF∥AB，GH∥BC，所以根据平行四边形的定义可以判定四边形ABFE是平行四边形，同理可判定四边形EFCD、四边形AGHD、四边形GBCH、四边形AGPE、四边形EPHD、四边形GBFP、四边形PFCH都是平行四边形，最后还要加上 ABCD，即共有9个平行四边形．导引：平行四边形的定义的功能：平行四边形的定义既是平行四边形的性质：平行四边形的两组对边分别平行；又是判定平行四边形的一种方法：两组对边分别平行的四边形是平行四边形．即对于任何一个几何定义，都具有两种功能，顺用是它的判定，逆用是它的性质．对于几何计数问题，要按照一定的顺序(如从小到大等)分类计数，做到不重复不遗漏．1. 如图，▱ABCD中，EF∥GH∥BC，MN∥AB，则图中平行四边形的个数是(　　)A．13 B．14 C．15 D．18D2. 如图，E，F分别是▱ABCD的边AD，BC上的点，EF＝6，∠DEF＝60°，将四边形EFCD沿EF翻折，得到四边形EFC′D′，ED′交BC于点G，则△GEF的周长为(　　)A．6 B．12 C．18 D．24C做一做(1)平行四边形是中心对称图形吗？如果是，你能找出它的对称中心并验证你的结论吗？知识点平行四边形的中心对称性 2平行四边形是中心对称图形，两条对角线的交点是它的对称中心.例2如图，已知过 ABCD的对角线BD上一点M分别作平行四边形两组对边的平行线EF与GH，则图中 AEMG的面积S1与 HCFM的面积S2的大小关系是(　　)A．S1＞S2　　　　　　　　B．S1＜S2C．S1＝S2 D．2S1＝S2C平行四边形是中心对称图形，平行四边形的对角线把平行四边形划分成两个全等三角形，这是解决此类问题的关键．1. 在平面直角坐标系中，已知▱ABCD的三个顶点坐标分别是A(a，b)，B(4，－2)，C(－a，－b)，则下列关于点D的说法正确的是(　　)甲：点D在第一象限乙：点D与点A关于原点对称丙：点D的坐标是(－4，2)丁：点D到原点距离是2A．甲乙 B．丙丁 C．甲丁 D．乙丙B做一做(2)你还发现平行四边形有哪些性质？我们还发现：平行四边形的对边相等、对角相等.请你尝试证明这些结论.知识点平行四边形的对边的性质3边的性质：平行四边形对边平行；平行四边形对边相等．数学表达式：如图，∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC，AB＝CD，AD＝BC.例3已知：如图(1)，四边形ABCD是平行四边形.求证：AB＝CD，BC＝DA. 连接AC(如图(2)).∵四边形ABCD是平行四边形，∴ AB∥CD，BC∥DA(平行四边形的定义）.∴∠1＝∠2,∠3＝∠4. ∵AC＝CA，∴△ABC≌△CDA. ∴AB＝CD，BC＝DA. 证明：例4已知：如图, 在▱ABCD中，E，F是对角线AC上的两点，并且AE＝CF.求证：BE=DF.证明：∵四边形ABCD是平行四边形，∴ AB＝CD(平行四边形的对边相等），AB∥CD(平行四边形的定义）.∴∠BAE＝∠DCF. 又∵AE＝CF，∴△ABE≌△CDF. ∴BE＝DF.如图，在▱ABCD中，对角线AC的垂直平分线分别交AD，BC于点E，F，连接CE，若△CED的周长为6，则▱ABCD的周长为(　　)A．6 B．12 C．18 D．241.B 如图，在▱ABCD中，BM是∠ABC的平分线，交CD于点M，且MC＝2，▱ABCD的周长是14，则DM等于(　　)A．1 B．2 C．3 D．42.C如图，在▱ABCD中，∠DAB的平分线交CD于点E，交BC的延长线于点G，∠ABC的平分线交CD于点F，交AD的延长线于点H，AG与BH交于点O，连接BE，下列结论错误的是(　　)A．BO＝OH B．DF＝CEC．DH＝CG D．AB＝AE3.D1. 角的性质：平行四边形对角相等；平行四边形邻角互补． 数学表达式：如图，∵四边形ABCD是平行四边形，∴∠A＝∠C，∠B＝∠D.∴∠A＋∠B＝180°，∠B＋∠C＝180°，∠C＋∠D＝180°，∠A＋∠D＝180°.知识点平行四边形角的性质3例5如图，在 ▱ ABCD中，已知∠A＋∠C＝120°，求平行四边形各角的度数．由平行四边形的对角相等，得∠A＝∠C，结合已知条件∠A＋∠C＝120°，即可求出∠A和∠C的度数；再根据平行线的性质，进而求出∠B，∠D的度数．导引：在 ▱ ABCD中，∠A＝∠C，∠B＝∠D.∵∠A＋∠C＝120°，∴∠A＝∠C＝60°.∴∠D＝180°－∠A＝180°－60°＝120°.∴∠B＝∠D＝120°.解：平行四边形中求有关角度的基本方法是利用平行四边形对角相等，邻角互补的性质，并且已知一个角或已知两邻角的关系可求出所有内角的度数．1. 已知平行四边形一个内角的度数，能确定其他内角的度数吗？说说你的理由.能确定其他内角的度数．理由：由平行四边形的定义和定理，得平行四边形邻角互补，对角相等，因此只要知道平行四边形一个内角的度数，就可确定其他内角的度数．解：2. 如图，四边形ABCD是平行四边形. 求：(1) ∠ADC和∠BCD的度数；(2)边AB和BC的长度.(1)因为∠B＝56°，且平行四边形的对角相等，邻角互补，所以∠ADC＝56°， ∠BCD＝180°－56°＝124°.(2)因为CD＝25，AD＝30， 且平行四边形的对边相等， 所以AB＝25，BC＝30.解：3. 如图，在▱ABCD中，连接AC，∠ABC＝∠CAD＝45°，AB＝2，则BC的长是(　　)A.B．2 C．2 D．4C4. 如图，在▱ABCD中，CE⊥AB，E为垂足，如果∠A＝120°，则∠BCE的度数是(　　)A．80° B．50° C．40° D．30°D5. 在▱ABCD中，∠A＋∠C＝200°，则∠B的度数是(　　)A．100° B．160° C．80° D．60°C1. [情境题·生活应用]如图，是马路边的三个停车位(车位线的对边互相平行)，则图中的平行四边形有 个.6　练点2 平行四边形的中心对称性 2. 如图，在平面直角坐标系中，▱ MNEF 的两条对角线 ME ， NF 交于原点 O ，点 F 的坐标是(3，2)，则点 N 的坐标是(　A　)A练点3 平行四边形的性质——对边平行且相等 3. [情境题·生活应用]如图是《亚洲－太平洋邮政联盟成立五十周年》纪念邮票，也是我国发行的首套平行四边形邮票，其相邻两边的长分别为44毫米和30毫米，则这枚邮票的周长为(　D　)D1.平行四边形的定义：两组对边分别平行的四边形.2.平行四边形具有中心对称性.3.平行四边形的对角相等.4.平行四边形的对角相等.在▱ABCD中，∠DAB的平分线分边BC为3 cm和4 cm两部分，则▱ABCD的周长为(　　)A．20 cm　 　　　　B．22 cmC．10 cm　 　　　　D．20 cm或22 cm易错点：不注意分情况讨论，造成漏解D点拨：情况一，如图①.BE＝3 cm，CE＝4 cm.∵四边形ABCD为平行四边形，∴AD＝BC，AB＝CD，AD∥BC.∴∠DAE＝∠AEB.∵AE平分∠BAD， ∴∠BAE＝∠DAE.∴∠BAE＝∠AEB. ∴AB＝BE＝3 cm.∴▱ABCD的周长＝(3＋3＋4)×2＝20(cm)．情况二，如图②.BE＝4 cm，CE＝3 cm.同理可得AB＝BE＝4 cm.∴▱ABCD的周长＝(4＋4＋3)×2＝22(cm)．本题运用了分类讨论思想，AE把BC分成3 cm和4 cm两部分，没有明确哪部分是3 cm，哪部分是4 cm，所以分两种情况．必做: 请完成教材课后练习 补充: 请完成本课时习题作业1作业2