





- 21.3 实际问题第2课时 平均变化率问题-2024-2025学年九年级数学上册教材配套同步课件(人教版) 课件 0 次下载
- 21.3 实际问题第3课时 降价促销问题-2024-2025学年九年级数学上册教材配套同步课件(人教版) 课件 0 次下载
- 22.1.1 二次函数-2024-2025学年九年级数学上册教材配套同步课件(人教版) 课件 0 次下载
- 22.1.2 二次函数y=ax²的图象和性质 第1课时(性质)-2024-2025学年九年级数学上册教材配套同步课件(人教版) 课件 0 次下载
- 22.1.2 二次函数y=ax²的图象和性质 第2课时(应用)-2024-2025学年九年级数学上册教材配套同步课件(人教版) 课件 0 次下载
数学九年级上册第二十一章 一元二次方程21.3 实际问题与一元二次方程集体备课ppt课件
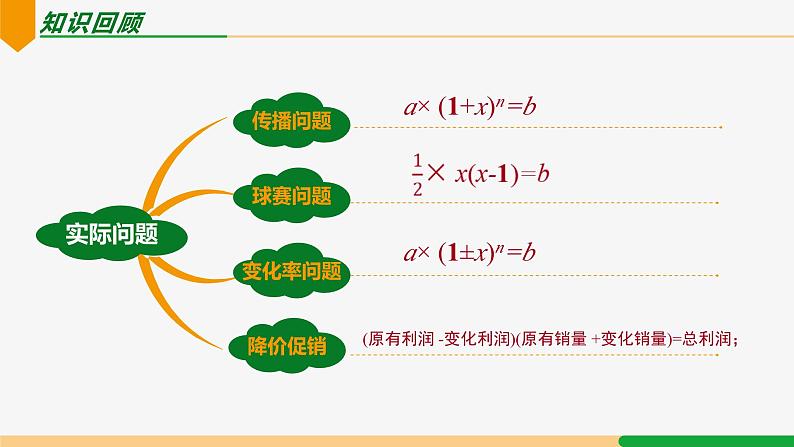
展开a× (1+x)n=b
a× (1±x)n=b
(原有利润 -变化利润)(原有销量 +变化销量)=总利润;
面积问题有什么数量关系 ?
例1:如图,在一块宽为 20 m,长为 32 m 的矩形地面上修筑同样宽的两条道路,余下的部分种上草坪,要使草坪的面积为 540 m2,则道路的宽为多少?
设道路的宽为 x m. 则
解法1:20×32-32x-20x+x2=540
解法2:设道路的宽为 x m. 则
(32 − x)(20 − x) = 540.
整理,得 x2 − 52x + 100 = 0.
解得 x1= 2,x2 = 50.
当 x = 50 时,32 − x = −18,不合题意,舍去.
答:道路的宽为 2 m.
变式1 在宽为 20 m,长为 32 m 的矩形地面上修筑如图所示的同样宽的道路,余下的部分种上草坪,要使草坪的面积为 540 m2,则这种方案下的道路的宽为多少?
解:设道路的宽为 x m,且 x<20.
(32 − x)(20 − x) = 540,
解得 x1 = 50 (舍去),x2 = 2.
变式3 在宽为 20 m,长为 32 m 的矩形地面上修筑如图所示的同样宽的道路,余下的部分种上草坪,要使草坪的面积为 540 m2,则这种方案下的道路的宽为多少?
解:设道路的宽为 x m,且 x<16.
(32 − 2x)(20 − x) = 540.
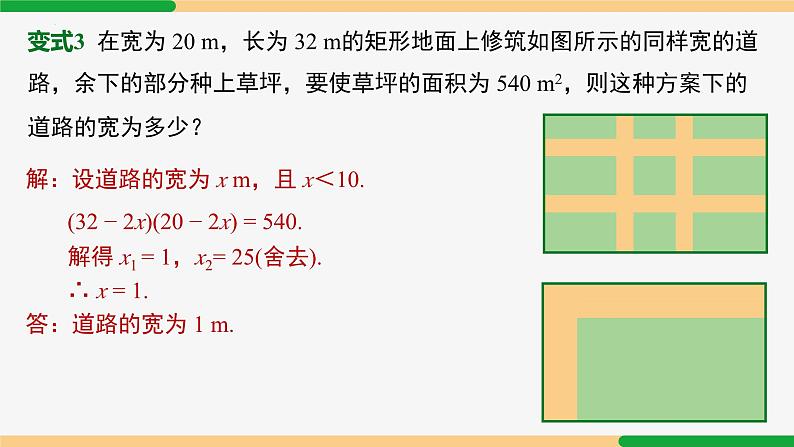
变式3 在宽为 20 m,长为 32 m的矩形地面上修筑如图所示的同样宽的道路,余下的部分种上草坪,要使草坪的面积为 540 m2,则这种方案下的道路的宽为多少?
解:设道路的宽为 x m,且 x<10.
(32 − 2x)(20 − 2x) = 540.
答:道路的宽为 1 m.
解得 x1 = 1,x2= 25(舍去).
变式4 在宽为 20 m,长为 32 m 的矩形地面上修筑四条道路,余下的部分种上草坪,如果横、纵小路的宽度比为 3∶2,且使小路所占面积是矩形面积的四分之一,则道路的宽为多少(保留两位小数)?
小路所占面积是矩形面积的四分之一
剩余面积是矩形面积的四分之三
解:设横、竖小路的宽度分别为 3x m、2x m,
∴ x≈0.62,则 3x≈1.86,2x≈1.24.
答:横、竖小路的宽度分别约为 1.86 m、1.24 m.
我们利用“图形经过移动,它的面积大小不会改变”的性质,把纵、横两条路移动一下,使列方程容易些(目的是求出小路的宽,至于实际施工,仍可按原图的位置修路)
解:设 AB 的长是 x m. 列方程,得 (58 − 2x)x = 200, 整理得 x2 − 29x + 100 = 0. 解得 x1 = 25,x2 = 4. 当 x = 25 时,58 − 2x = 8; 当 x = 4 时,58 − 2x = 50.答:羊圈的边 AB 和 BC 的长各是 25 m,8 m 或 4 m,50 m.
例2 如图,要利用一面墙(墙足够长)建羊圈,用 58 m的围栏围成面积为 200 m2 的矩形羊圈,则羊圈的边 AB 和 BC 的长各是多少米?
解:设 AB 的长是 x m. 列方程,得 (80 − 2x)x = 600. 整理得 x2 − 40x + 300 = 0, 解得 x1 = 10,x2 = 30. 当 x = 10 时,80 − 2x = 60 > 25(舍去); 当 x = 30 时,80 − 2x = 20 < 25.答:羊圈的边 AB 和 BC 的长各是 30 m,20 m.
变式1 如图,要利用一面墙 (墙长为 25 m) 建羊圈,用 80 m 的围栏围成面积为 600 m2 的矩形羊圈,则羊圈的边 AB 和 BC 的长各是多少米?
变式3 如图,一农户要建一个矩形鸡场,鸡场的一边利用长为 12 m 的住房墙,另外三边用 25 m 长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个 1 m 的门,所围鸡场的长、宽分别为多少时,面积为 80 m2?
解:设矩形鸡场垂直于住房墙的一边长为 x m,
由题意得 x(25 − 2x + 1) = 80,
解得 x1 = 5,x2 = 8.
当 x = 5 时,26 − 2x = 16 > 12(舍去);
当 x = 8 时,26 − 2x = 10 < 12.
故所围矩形鸡场的长为 10 m,宽为 8 m.
则平行于住房墙的一边长 (25 − 2x + 1) m.
一般先设其中的一条边为 x,然后用含 x 的代数式表示另一边,最后根据面积或周长公式列方程求解. 需要注意联系实际问题选择合适的解.
图形经过移动,它的面积大小不会改变
设其中的一条边为 x,然后用含 x 的代数式表示另一边,最后根据面积或周长公式列方程求解
1. 在一幅长 80 cm,宽 50 cm 的长方形风景画的四周镶一条金色纸边,制成一幅长方形挂图,如图所示,如果要使整个挂图的面积是 5400 cm2,设金色纸边的宽为 x cm,那么 x 满足的方程是( )A.x2 + 130x - 1400 = 0B.x2 + 65x - 350 = 0C.x2 - 130x - 1400 = 0D.x2 - 65x - 350 = 0
1. 某校准备修建一个面积为180平方米的矩形活动场地,它的长比宽多11米,设场地的宽为x米,则可列方程为( )A.x(x-11)=180 B.2x+2(x-11)=180C.x(x+11)=180 D.2x+2(x+11)=180
2. 公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1 m,另一边减少了2m,剩余空地的面积为18 m2,求原正方形空地的边长.设原正方形空地的边长为x m,则可列方程为( )A.(x+1)(x+2)=18 B.x2-3x+16=0C.(x-1)(x-2)=18 D.x2+3x+16=0
2. 一块矩形铁板,长是宽的 2 倍,如果在 4 个角上截去边长为 5 cm 的小正方形,然后把四边折起来,做成一个没有盖的盒子,盒子的容积是 3000 cm3,求铁板的长和宽.
解:设铁板的宽为 x cm,则长为 2x cm.
列方程,得 5(2x − 10)(x − 10) = 3000,整理,得 x2 − 15x − 250 = 0.解得 x1 = 25,x2 = −10 (舍去),所以 2x = 50.
答:铁板的长为 50 cm,宽为 25 cm.
初中数学人教版(2024)九年级上册21.3 实际问题与一元二次方程教课内容ppt课件: 这是一份初中数学人教版(2024)九年级上册<a href="/sx/tb_c10284_t3/?tag_id=26" target="_blank">21.3 实际问题与一元二次方程教课内容ppt课件</a>,共19页。PPT课件主要包含了实际问题,传播问题,球赛问题,变化率问题,知识要点1,降价促销,进货量为等内容,欢迎下载使用。
初中数学人教版(2024)九年级上册21.3 实际问题与一元二次方程集体备课课件ppt: 这是一份初中数学人教版(2024)九年级上册<a href="/sx/tb_c10284_t3/?tag_id=26" target="_blank">21.3 实际问题与一元二次方程集体备课课件ppt</a>,共19页。PPT课件主要包含了实际问题,传播问题,球赛问题,握手问题,赠物问题,树支问题,繁殖问题,知识要点1,解方程得,整理方程得等内容,欢迎下载使用。
初中数学21.3 实际问题与一元二次方程集体备课课件ppt: 这是一份初中数学<a href="/sx/tb_c10284_t3/?tag_id=26" target="_blank">21.3 实际问题与一元二次方程集体备课课件ppt</a>,共17页。PPT课件主要包含了传染源1,知识要点1,传播问题数量关系,解方程得,不合题意舍去,经过第3轮传播得,主干1,支干x,小分支x2,实际问题等内容,欢迎下载使用。













