三年（2022-2024）高考数学真题分类汇编（全国通用）专题02 函数的概念与基本初等函数Ⅰ（八大考点）（解析版）

这是一份三年（2022-2024）高考数学真题分类汇编（全国通用）专题02 函数的概念与基本初等函数Ⅰ（八大考点）（解析版），共19页。试卷主要包含了若为偶函数，则 等内容，欢迎下载使用。

考点1：已知奇偶性求参数
1．（2023年新课标全国Ⅱ卷数学真题）若为偶函数，则（ ）．
A．B．0C．D．1
【答案】B
【解析】因为 为偶函数，则 ，解得，
当时，，，解得或，
则其定义域为或，关于原点对称.
，
故此时为偶函数.
故选：B.
2．（2023年高考全国乙卷数学（理）真题）已知是偶函数，则（ ）
A．B．C．1D．2
【答案】D
【解析】因为为偶函数，则，
又因为不恒为0，可得，即，
则，即，解得.
故选：D.
3．（2024年上海夏季高考数学真题）已知，，且是奇函数，则 ．
【答案】
【解析】因为是奇函数，故即，
故，
故答案为：.
4．（2022年高考全国乙卷数学（文）真题）若是奇函数，则 ， ．
【答案】 ； ．
【解析】[方法一]：奇函数定义域的对称性
若，则的定义域为，不关于原点对称
若奇函数的有意义，则且
且，
函数为奇函数，定义域关于原点对称，
，解得，
由得，，
，
故答案为：；．
[方法二]：函数的奇偶性求参
函数为奇函数
[方法三]：
因为函数为奇函数，所以其定义域关于原点对称．
由可得，，所以，解得：，即函数的定义域为，再由可得，．即，在定义域内满足，符合题意．
故答案为：；．
5．（2023年高考全国甲卷数学（理）真题）若为偶函数，则 ．
【答案】2
【解析】因为为偶函数，定义域为，
所以，即，
则，故，
此时，
所以，
又定义域为，故为偶函数，
所以.
故答案为：2.
考点2：函数图像的识别
6．（2022年新高考天津数学高考真题）函数的图像为（ ）
A．B．
C．D．
【答案】D
【解析】函数的定义域为，
且，
函数为奇函数，A选项错误；
又当时，，C选项错误；
当时，函数单调递增，故B选项错误；
故选：D.
7．（2023年天津高考数学真题）已知函数的部分图象如下图所示，则的解析式可能为（ ）

A．B．
C．D．
【答案】D
【解析】由图知：函数图象关于y轴对称，其为偶函数，且，
由且定义域为R，即B中函数为奇函数，排除；
当时、，即A、C中上函数值为正，排除；
故选：D
8．（2024年高考全国甲卷数学（理）真题）函数在区间的图象大致为（ ）
A．B．
C．D．
【答案】B
【解析】，
又函数定义域为，故该函数为偶函数，可排除A、C，
又，
故可排除D.
故选：B.
9．（2024年新课标全国Ⅰ卷数学真题）当时，曲线与的交点个数为（ ）
A．3B．4C．6D．8
【答案】C
【解析】因为函数的的最小正周期为，
函数的最小正周期为，
所以在上函数有三个周期的图象，
在坐标系中结合五点法画出两函数图象，如图所示：
由图可知，两函数图象有6个交点.
故选：C
10．（2022年高考全国乙卷数学（文）真题）如图是下列四个函数中的某个函数在区间的大致图像，则该函数是（ ）
A．B．C．D．
【答案】A
【解析】设，则，故排除B;
设，当时，，
所以，故排除C;
设，则，故排除D.
故选：A.
11．（2022年高考全国甲卷数学（理）真题）函数在区间的图象大致为（ ）
A．B．
C．D．
【答案】A
【解析】令，
则，
所以为奇函数，排除BD；
又当时，，所以，排除C.
故选：A.
考点3：函数的实际应用
12．（2022年新高考北京数学高考真题）在北京冬奥会上，国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术，为实现绿色冬奥作出了贡献．如图描述了一定条件下二氧化碳所处的状态与T和的关系，其中T表示温度，单位是K；P表示压强，单位是．下列结论中正确的是（ ）
A．当，时，二氧化碳处于液态
B．当，时，二氧化碳处于气态
C．当，时，二氧化碳处于超临界状态
D．当，时，二氧化碳处于超临界状态
【答案】D
【解析】当，时，，此时二氧化碳处于固态，故A错误.
当，时，，此时二氧化碳处于液态，故B错误.
当，时，与4非常接近，故此时二氧化碳处于固态，对应的是非超临界状态，故C错误.
当，时，因, 故此时二氧化碳处于超临界状态，故D正确.
故选：D
13．（2024年北京高考数学真题）生物丰富度指数 是河流水质的一个评价指标，其中分别表示河流中的生物种类数与生物个体总数.生物丰富度指数d越大，水质越好．如果某河流治理前后的生物种类数没有变化，生物个体总数由变为，生物丰富度指数由提高到，则（ ）
A．B．
C． D．
【答案】D
【解析】由题意得，则，即，所以.
故选：D.
14．（多选题）（2023年新课标全国Ⅰ卷数学真题）噪声污染问题越来越受到重视．用声压级来度量声音的强弱，定义声压级，其中常数是听觉下限阈值，是实际声压．下表为不同声源的声压级：
已知在距离燃油汽车、混合动力汽车、电动汽车处测得实际声压分别为，则（ ）．
A．B．
C．D．
【答案】ACD
【解析】由题意可知：，
对于选项A：可得，
因为，则，即，
所以且，可得，故A正确；
对于选项B：可得，
因为，则，即，
所以且，可得，
当且仅当时，等号成立，故B错误；
对于选项C：因为，即，
可得，即，故C正确；
对于选项D：由选项A可知：，
且，则，
即，可得，且，所以，故D正确；
故选：ACD.
考点4：基本初等函数的性质：单调性、奇偶性
15．（2023年高考全国乙卷数学（理）真题）设，若函数在上单调递增，则a的取值范围是 .
【答案】
【解析】由函数的解析式可得在区间上恒成立，
则，即在区间上恒成立，
故，而，故，
故即，故，
结合题意可得实数的取值范围是.
故答案为：.
16．（2022年新高考北京数学高考真题）已知函数，则对任意实数x，有（ ）
A．B．
C．D．
【答案】C
【解析】，故A错误，C正确；
，不是常数，故BD错误；
故选：C．
17．（2023年北京高考数学真题）下列函数中，在区间上单调递增的是（ ）
A．B．
C．D．
【答案】C
【解析】对于A，因为在上单调递增，在上单调递减，
所以在上单调递减，故A错误；
对于B，因为在上单调递增，在上单调递减，
所以在上单调递减，故B错误；
对于C，因为在上单调递减，在上单调递减，
所以在上单调递增，故C正确；
对于D，因为，，
显然在上不单调，D错误.
故选：C.
18．（2024年新课标全国Ⅰ卷数学真题）已知函数在R上单调递增，则a的取值范围是（ ）
A．B．C．D．
【答案】B
【解析】因为在上单调递增，且时，单调递增，
则需满足，解得，
即a的范围是.
故选：B.
19．（2024年天津高考数学真题）下列函数是偶函数的是（ ）
A．B．C．D．
【答案】B
【解析】对A，设，函数定义域为，但，，则，故A错误；
对B，设，函数定义域为，
且，则为偶函数，故B正确；
对C，设，函数定义域为，不关于原点对称， 则不是偶函数，故C错误；
对D，设，函数定义域为，因为，，
则，则不是偶函数，故D错误.
故选：B.
20．（2023年新课标全国Ⅰ卷数学真题）设函数在区间上单调递减，则的取值范围是（ ）
A．B．
C．D．
【答案】D
【解析】函数在R上单调递增，而函数在区间上单调递减，
则有函数在区间上单调递减，因此，解得，
所以的取值范围是.
故选：D
考点5：分段函数问题
21．（2022年新高考浙江数学高考真题）已知函数则 ；若当时，，则的最大值是 ．
【答案】 /
【解析】由已知，，
所以，
当时，由可得，所以，
当时，由可得，所以，
等价于，所以，
所以的最大值为.
故答案为：，.
22．（2024年上海夏季高考数学真题）已知则 ．
【答案】
【解析】因为故，
故答案为：.
考点6：函数的定义域、值域、最值问题
23．（2022年新高考北京数学高考真题）函数的定义域是 ．
【答案】
【解析】因为，所以，解得且，
故函数的定义域为；
故答案为：
24．（2022年新高考北京数学高考真题）设函数若存在最小值，则a的一个取值为 ；a的最大值为 ．
【答案】 0（答案不唯一） 1
【解析】若时，，∴；
若时，当时，单调递增，当时，，故没有最小值，不符合题目要求；
若时，
当时，单调递减，，
当时，
∴或，
解得，
综上可得；
故答案为：0（答案不唯一），1
考点7：函数性质（对称性、周期性、奇偶性）的综合运用
25．（多选题）（2023年新课标全国Ⅰ卷数学真题）已知函数的定义域为，，则（ ）．
A．B．
C．是偶函数D．为的极小值点
【答案】ABC
【解析】方法一：
因为，
对于A，令，，故正确.
对于B，令，，则，故B正确.
对于C，令，，则，
令，
又函数的定义域为，所以为偶函数，故正确，
对于D，不妨令，显然符合题设条件，此时无极值，故错误.
方法二：
因为，
对于A，令，，故正确.
对于B，令，，则，故B正确.
对于C，令，，则，
令，
又函数的定义域为，所以为偶函数，故正确，
对于D，当时，对两边同时除以，得到，
故可以设，则，
当肘，，则，
令，得；令，得；
故在上单调递减，在上单调递增，
因为为偶函数，所以在上单调递增，在上单调递减，
显然，此时是的极大值，故D错误.
故选：.
26．（多选题）（2022年新高考全国I卷数学真题）已知函数及其导函数的定义域均为，记，若，均为偶函数，则（ ）
A．B．C．D．
【答案】BC
【解析】[方法一]：对称性和周期性的关系研究
对于，因为为偶函数，所以即①，所以，所以关于对称，则，故C正确；
对于，因为为偶函数，，，所以关于对称，由①求导，和，得，所以，所以关于对称，因为其定义域为R，所以，结合关于对称，从而周期，所以，，故B正确，D错误；
若函数满足题设条件，则函数（C为常数）也满足题设条件，所以无法确定的函数值，故A错误.
故选：BC.
[方法二]：【最优解】特殊值，构造函数法.
由方法一知周期为2，关于对称，故可设，则，显然A，D错误，选BC.
故选：BC.
[方法三]：
因为，均为偶函数，
所以即，，
所以，，则，故C正确；
函数，的图象分别关于直线对称，
又，且函数可导，
所以，
所以，所以，
所以，，故B正确，D错误；
若函数满足题设条件，则函数（C为常数）也满足题设条件，所以无法确定的函数值，故A错误.
故选：BC.
【点评】方法一：根据题意赋值变换得到函数的性质，即可判断各选项的真假，转化难度较高，是该题的通性通法；
方法二：根据题意得出的性质构造特殊函数，再验证选项，简单明了，是该题的最优解．
27．（2024年新课标全国Ⅰ卷数学真题）已知函数的定义域为R，，且当时，则下列结论中一定正确的是（ ）
A．B．
C．D．
【答案】B
【解析】因为当时，所以，
又因为，
则，
，
，
，
，则依次下去可知，则B正确；
且无证据表明ACD一定正确.
故选：B.
28．（2022年新高考全国II卷数学真题）已知函数的定义域为R，且，则（ ）
A．B．C．0D．1
【答案】A
【解析】[方法一]：赋值加性质
因为，令可得，，所以，令可得，，即，所以函数为偶函数，令得，，即有，从而可知，，故，即，所以函数的一个周期为．因为，，，，，所以
一个周期内的．由于22除以6余4，
所以．故选：A．
[方法二]：【最优解】构造特殊函数
由，联想到余弦函数和差化积公式
，可设，则由方法一中知，解得，取，
所以，则
，所以符合条件，因此的周期，，且，所以，
由于22除以6余4，
所以．故选：A．
【整体点评】法一：利用赋值法求出函数的周期，即可解出，是该题的通性通法；
29．（2022年高考全国乙卷数学（理）真题）已知函数的定义域均为R，且．若的图像关于直线对称，，则（ ）
A．B．C．D．
【答案】D
【解析】因为的图像关于直线对称，
所以，
因为，所以，即，
因为，所以，
代入得，即，
所以，
.
因为，所以，即，所以.
因为，所以，又因为，
联立得，，
所以的图像关于点中心对称，因为函数的定义域为R，
所以
因为，所以.
所以.
故选：D
考点8：指对幂运算
30．（2022年新高考天津数学高考真题）化简的值为（ ）
A．1B．2C．4D．6
【答案】B
【解析】原式
，
故选：B
31．（2022年新高考浙江数学高考真题）已知，则（ ）
A．25B．5C．D．
【答案】C
【解析】因为，，即，所以．
故选：C.
32．（2024年高考全国甲卷数学（理）真题）已知且，则 ．
【答案】64
【解析】由题，整理得，
或，又，
所以，故
故答案为：64.
33．（2023年北京高考数学真题）已知函数，则 ．
【答案】1
【解析】函数，所以.
故答案为：1
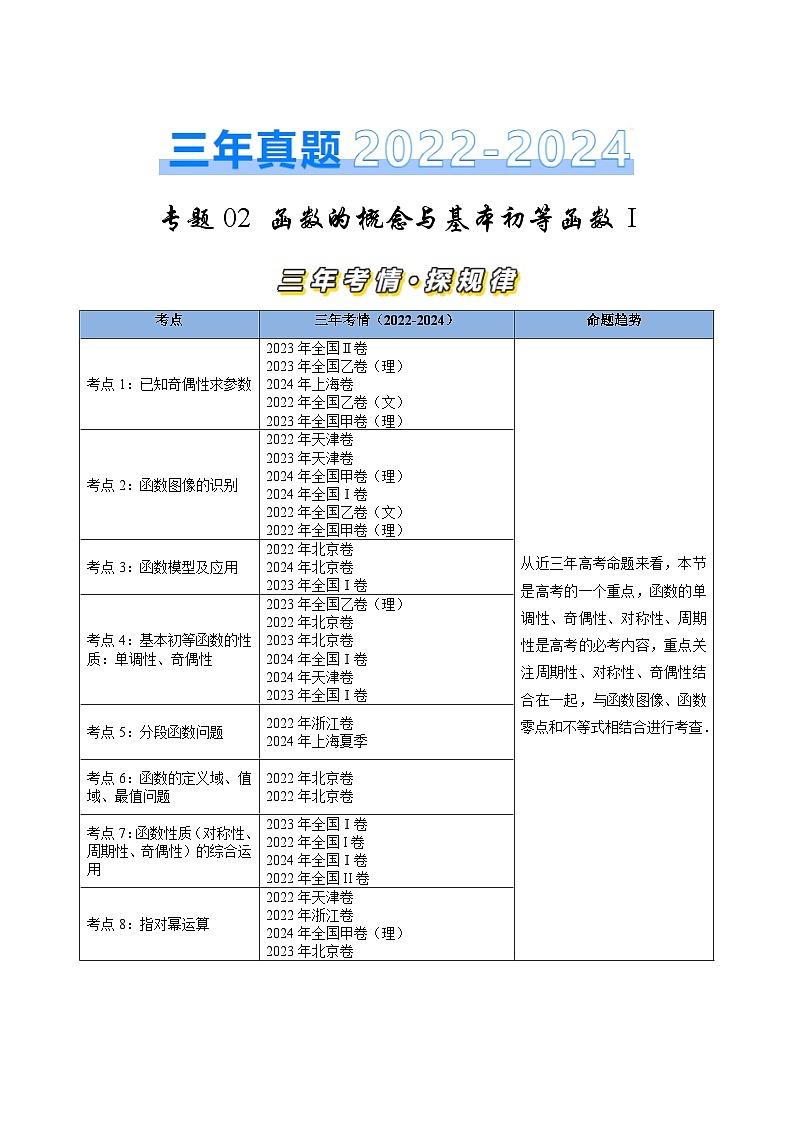
考点
三年考情（2022-2024）
命题趋势
考点1：已知奇偶性求参数
2023年全国Ⅱ卷
2023年全国乙卷（理）
2024年上海卷
2022年全国乙卷（文）
2023年全国甲卷（理）
从近三年高考命题来看，本节是高考的一个重点，函数的单调性、奇偶性、对称性、周期性是高考的必考内容，重点关注周期性、对称性、奇偶性结合在一起，与函数图像、函数零点和不等式相结合进行考查．
考点2：函数图像的识别
2022年天津卷
2023年天津卷
2024年全国甲卷（理）
2024年全国Ⅰ卷
2022年全国乙卷（文）
2022年全国甲卷（理）
考点3：函数模型及应用
2022年北京卷
2024年北京卷
2023年全国Ⅰ卷
考点4：基本初等函数的性质：单调性、奇偶性
2023年全国乙卷（理）
2022年北京卷
2023年北京卷
2024年全国Ⅰ卷
2024年天津卷
2023年全国Ⅰ卷
考点5：分段函数问题
2022年浙江卷
2024年上海夏季
考点6：函数的定义域、值域、最值问题
2022年北京卷
2022年北京卷
考点7：函数性质（对称性、周期性、奇偶性）的综合运用
2023年全国Ⅰ卷
2022年全国I卷
2024年全国Ⅰ卷
2022年全国II卷
考点8：指对幂运算
2022年天津卷
2022年浙江卷
2024年全国甲卷（理）
2023年北京卷
声源
与声源的距离
声压级
燃油汽车
10
混合动力汽车
10
电动汽车
10
40