第22章 二次函数小结第3课时 专题二 二次函数与实际问题-2024-2025学年九年级数学上册教材配套同步课件（人教版）

这是一份第22章 二次函数小结第3课时 专题二 二次函数与实际问题-2024-2025学年九年级数学上册教材配套同步课件（人教版），共18页。

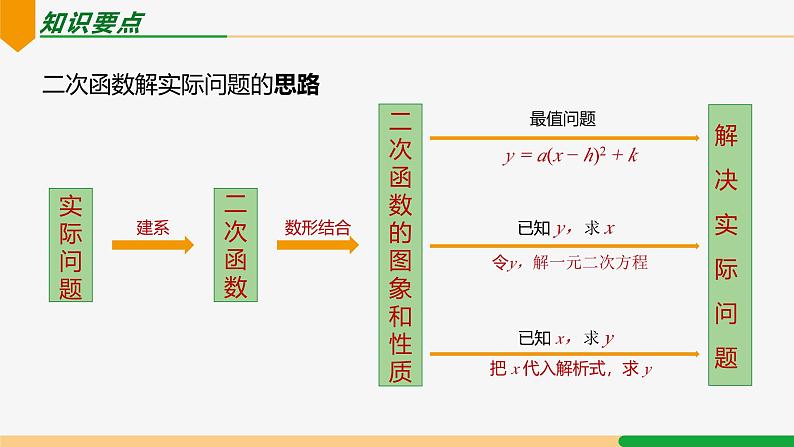
二次函数与实际问题第22章 小结与复习| 第3课时|专题内容专题二：二次函数与销售问题专题三：二次函数与分段函数问题专题一：二次函数与面积问题知识要点二次函数解实际问题的思路实际问题二次函数二次函数的图象和性质解决实际问题最值问题 y = a(x − h)2 + k 已知 y，求 x 令y，解一元二次方程 已知 x，求 y 把 x 代入解析式，求 y建系数形结合专题一：二次函数与面积问题例1. 张大伯准备用 40 m 长的木栏围一个矩形的菜园，为了节约材料同时要使矩形的面积最大，他利用自家房屋一面长 25 m 的墙，设计了如图一个矩形的菜园.(1)请你求出张大伯矩形菜园的面积；(2)请你判断他的设计方案是否合理？如果合理，直接答合理；如果不合理又该如何设计？并说明理由.解：(1) 由题意得菜园的长为 25 m，宽为(40 - 25)÷2 = 7.5 (m).故菜园的面积为 25×7.5 = 187.5 ( m2 )(2)请你判断他的设计方案是否合理？如果合理，直接答合理；如果不合理又该如何设计？并说明理由.(2) 设菜园与墙垂直的一边为 x m，则与墙相对的一边长为(40 - 2x)m，菜园的面积 S = x(40 - 2x) = -2x2 + 40x = -2(x -10)2 + 200 (7.5≤x＜20).∵7.5≤10＜20，所以当 x = 10 时，S 有最大值，此时 S = 200. 故张大伯的设计不合理.菜园与墙垂直的两边长为 10 m，而与墙相对的一边长为 (40 - 2x) m = 20 m.专题二：二次函数与销售问题例2.一家电脑公司推出一款新型电脑，投放市场以来 3 个月的利润情况如图所示，该图可以近似看作为抛物线的一部分，请结合图象，解答以下问题：(1) 求该抛物线对应的二次函数解析式；(2)该公司在经营此款电脑过程中，第几月的利润最大？最大利润是多少？(3)若照此经营下去，请你结合所学的知识，对公司在此款电脑的经营状况(是否亏损？何时亏损？)作预测分析.解：(1)因图象过原点，则设函数解析式为 y = ax2 + bx,得故所求二次函数的解析式为 y = −x2 + 14x.解得 a = −1，b = 14.(2) y = −x2 + 14x = −(x − 7)2 + 49. 即当 x = 7 时，利润最大，y = 49.(3) 没有利润，即 y = −x2 +14x = 0. 解得 x1 = 0 (舍去)，或 x2 = 14，而这时利润为滑坡状态，所以第 15 个月，公司亏损.专题三：二次函数与分段函数问题例3. 某市某乡镇在“精准扶贫”活动中销售一农产品，经分析发现月销售量 y (万件) 与月份 x (月) 的关系为： 每件产品的利润z (元) 与月份 x (月) 的关系如下表：(1) 请你根据表格求出每件产品利润 z (元) 与月份 x (月)的关系式；(2) 若月利润 w(万元)＝当月销售量 y (万件)×当月每件产品的利润 z (元)，求月利润 w (万元) 与月份 x (月)的关系式；(3) 当 x 为何值时，月利润 w 有最大值，最大值为多少？ 解：(1) 当 1≤x≤9 时，设每件产品利润 z (元)与月份 x (月)的关系式为 z＝kx + b，则： ，得 ，即当 1≤x≤9 时，每件产品利润 z (元) 与月份 x (月) 的关系式为 z＝﹣x + 20，当 10≤x≤12 时，z＝10，由上可得，(2) 当 1≤x≤8 时， w＝ (x + 4)(-x + 20)＝-x2 + 16x + 80；当 x＝9 时，w＝(-9 + 20)×(-9 + 20)＝121；当 10≤x≤12 时，w＝ (-x + 20)×10＝-10x + 200，综上可知，(3) 当 1≤x≤8 时，w＝-x2 + 16x + 80＝-(x﹣8)2 + 144，∴当 x＝8 时，w 取得最大值，此时 w＝144；当 x＝9 时，w＝121；当 10≤x≤12 时，w＝-10x + 200，则当 x＝10 时，w 取得最大值，此时 w＝100，由上可得，当 x 为 8 时，月利润 w 有最大值，最大值144 万元． 课堂练习1. 荆州市某水产养殖户进行小龙虾养殖．已知每千克小龙虾养殖成本为 6 元，在整个销售旺季的 80 天里，销售单价 p (元/千克)与时间第 t (天) 之间的函数关系为：日销售量 y (千克) 与时间第 t (天)之间的函数关系如图所示：(1) 求日销售量 y 与时间 t 的函数关系式？(2) 哪一天的日销售利润最大？最大利润是多少？(3) 该养殖户有多少天日销售利润不低于 2400 元？(4) 在实际销售的前 40 天中，该养殖户决定每销售 1 千克小龙虾，就捐赠 m (m＜7) 元给村里的特困户．在这前 40 天中，每天扣除捐赠后的日销售利润随时间 t 的增大而增大，求 m 的取值范围．解：(1) 设解析式为 y＝kt + b，将(1，198)、(80，40)代入，得 解得 ，∴ y＝﹣2t + 200 (1≤t≤80，t 为整数).(2) 设日销售利润为 w，则 w＝(p﹣6)y，①当 1≤t≤40 时，∴当 t＝30 时，w最大＝2450；②当 41≤t≤80 时， ∴当 t＝41 时，w最大＝2301，∵ 2450＞2301，∴ 第 30 天的日销售利润最大，最大利润为 2450 元．(3) 由 (2) 得：当 1≤t≤40 时，令 w＝2400，即解得 t1＝20 或 t2＝40. 由函数 图象可知，当 20≤t≤40 时，日销售利润不低于 2400 元，而当 41≤t≤80 时，w最大＝2301＜2400，∴ t 的取值范围是20≤t≤40 ，∴ 共有 21 天符合条件．(4) 设日销售利润为 w，根据题意，得其函数图象的对称轴为 t＝2m + 30，∵ w 随 t 的增大而增大，且 1≤t≤40，t 为整数.∴由二次函数的图象及其性质可知 2m + 30＞39.5， 解得 m＞ ， 又 m＜7，∴ ＜m＜7．