初中人教版（2024）22.2二次函数与一元二次方程公开课ppt课件

这是一份初中人教版（2024）22.2二次函数与一元二次方程公开课ppt课件，共16页。PPT课件主要包含了课堂导航，知识回顾，数形结合，有两个公共点，有两个不相等的实数根，Δ＞0，有一个公共点，有两个相等的实数根，没有公共点，没有实数根等内容，欢迎下载使用。

利用二次函数求一元二次方程的近似根.会判断抛物线中常量的符号
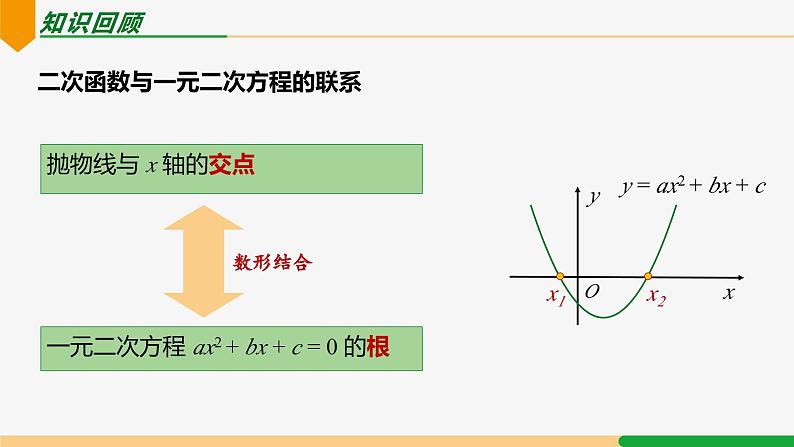
抛物线与 x 轴的交点
一元二次方程 ax2 + bx + c = 0 的根
y = ax2 + bx + c
二次函数与一元二次方程的联系
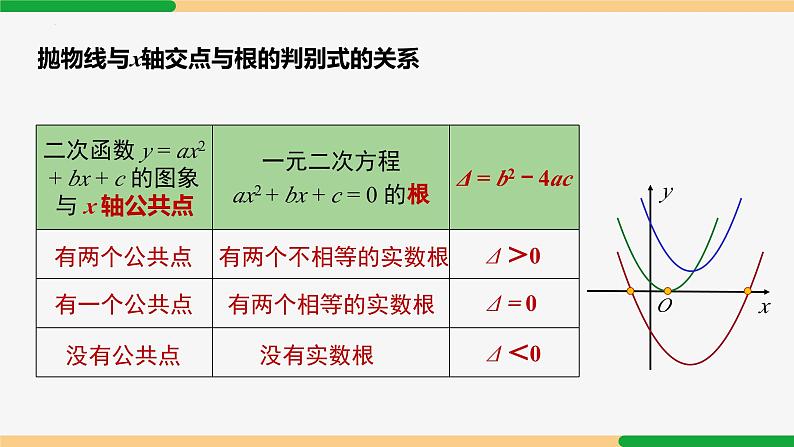
抛物线与x轴交点与根的判别式的关系
例1 利用函数图象求方程 x2 − 2x − 2 = 0 的实数根(结果保留小数点后一位).
解：画出函数 y = x² − 2x − 2 的图象(如下图)，则方程有两个实数根，一个在 −1 与 0之间，另一个在 2 与 3 之间.
通过取平均数的方法不断缩小根的范围.
y = -0.75＜0
y = 0.062 5＞0
所以跟在 2.5 和 2.75 之间，然后重复上述步骤.
最终，根在 2.687 5 和 2.75 之间，要求精确到 0.1.
故取 x1≈2.7.
同理可得另一近似根为 x2≈-0.7.
3. 已知二次函数 y＝ax2＋bx＋c 的图象如图所示，则一元二次方程 ax2＋bx＋c＝0 的近似根为 (　　)A. x1≈－2.1，x2≈0.1 B. x1≈－2.5，x2≈0.5C. x1≈－2.9，x2≈0.9 D. x1≈－3， x2≈1
例2 在图中画出函数y=x2-2x-3的图象，利用图象回答:(1)方程x2-2x-3=0的解是多少；(2) x取什么值时，函数值大于0；(3) x取什么值时，函数值小于0.
解：图象如图所示.(1) 方程x2-2x-3=0的解为x1=-1，x2=3.(2) x>3或x<-1时，函数值大于0.(3) -1例4 如图，已知二次函数 y＝ax2＋bx＋c 图象的对称轴为直线 x＝-1，下列结论：①abc＜0；②3a＜-c；③若 m 为任意实数，则有 a - bm＜am2 + b；④若图象经过点(-3，-2)，方程 a2 + bx + c + 2 = 0 的两根为 x1，x2 ( | x1 |＜| x2 | )，则 2x1－x2 = 5.其中正确的结论的个数是 (　　) A．1　　　B．2　　　　C．3　　　D．4
二次函数y= ax2 + bx + c 与 x 轴的交点
根据函数图象求一元二次方程的近似解
可知方程 ax2 + bx + c = 0 (a ≠ 0，a，b，c 为常数) 的一个解 x1 的范围是（ ） A. 3 ＜ x1 ＜ 3.23 B. 3.23 ＜ x1 ＜ 3.24 C. 3.24 ＜ x1 ＜ 3.25 D. 3.25 ＜ x1 ＜ 3.26
1. 根据下列表格的对应值：
2. 若一元二次方程 x2 - mx + n = 0 无实根，则抛物线 y = x2 - mx + n 图象位于( ) A. x 轴上方 B. 第一、二、三象限 C. x 轴下方 D. 第二、三、四象限