

- 专题27 等差数列及其前n项和9题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测(原卷版) 试卷 0 次下载
- 专题27 等差数列及其前n项和9题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测(解析版) 试卷 0 次下载
- 专题28 等比数列及其前n项和9题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测(解析版) 试卷 0 次下载
- 专题29 求数列的通项公式10题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测(原卷版) 试卷 0 次下载
- 专题29 求数列的通项公式10题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测(解析版) 试卷 0 次下载
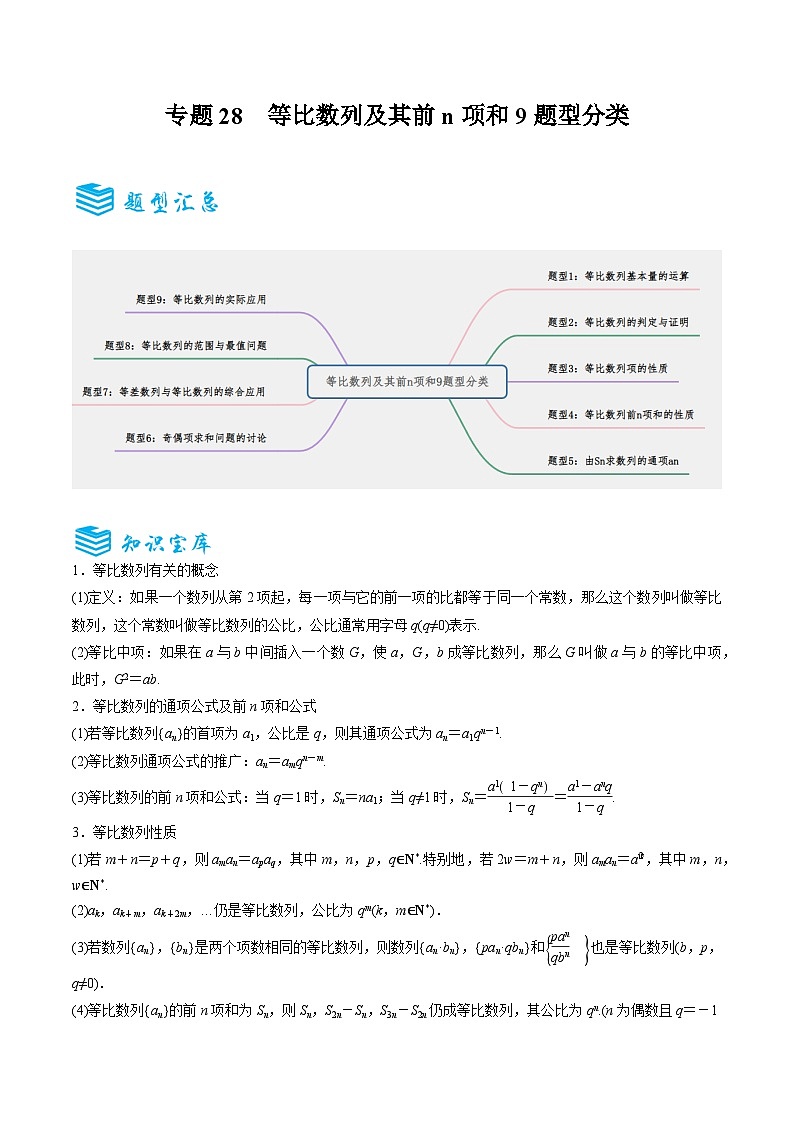
专题28 等比数列及其前n项和9题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测(原卷版)
展开1.等比数列有关的概念
(1)定义:如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q(q≠0)表示.
(2)等比中项:如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项,此时,G2=ab.
2.等比数列的通项公式及前n项和公式
(1)若等比数列{an}的首项为a1,公比是q,则其通项公式为an=a1qn-1.
(2)等比数列通项公式的推广:an=amqn-m.
(3)等比数列的前n项和公式:当q=1时,Sn=na1;当q≠1时,Sn=eq \f(a11-qn,1-q)=eq \f(a1-anq,1-q).
3.等比数列性质
(1)若m+n=p+q,则aman=apaq,其中m,n,p,q∈N*.特别地,若2w=m+n,则aman=aeq \\al(2,w),其中m,n,w∈N*.
(2)ak,ak+m,ak+2m,…仍是等比数列,公比为qm(k,m∈N*).
(3)若数列{an},{bn}是两个项数相同的等比数列,则数列{an·bn},{pan·qbn}和eq \b\lc\{\rc\}(\a\vs4\al\c1(\f(pan,qbn)))也是等比数列(b,p,q≠0).
(4)等比数列{an}的前n项和为Sn,则Sn,S2n-Sn,S3n-S2n仍成等比数列,其公比为qn.(n为偶数且q=-1除外)
(5)若eq \b\lc\{\rc\ (\a\vs4\al\c1(a1>0,,q>1))或eq \b\lc\{\rc\ (\a\vs4\al\c1(a1<0,,0
常用结论
1.等比数列{an}的通项公式可以写成an=cqn,这里c≠0,q≠0.
2.等比数列{an}的前n项和Sn可以写成Sn=Aqn-A(A≠0,q≠1,0).
3.数列{an}是等比数列,Sn是其前n项和.
(1)若a1·a2·…·an=Tn,则Tn,eq \f(T2n,Tn),eq \f(T3n,T2n),…成等比数列.
(2)若数列{an}的项数为2n,则eq \f(S偶,S奇)=q;若项数为2n+1,则eq \f(S奇-a1,S偶)=q,或eq \f(S偶,S奇-an)=q.
一、单选题
1.(2024·浙江温州·模拟预测)已知等比数列的前n项和为,公比为q,且,则( )
A.B.C.D.
2.(2024·全国)设等比数列的各项均为正数,前n项和,若,,则( )
A.B.C.15D.40
3.(2024·江西抚州·模拟预测)已知正项等比数列{}的前n项和为,若,则=( )
A.64B.81C.128D.192
4.(2024·江西·模拟预测)已知等比数列的前4项和为,,则( )
A.B.C.1D.2
5.(2024·上海闵行·二模)已知数列为等比数列,首项,公比,则下列叙述不正确的是( )
A.数列的最大项为B.数列的最小项为
C.数列为严格递增数列D.数列为严格递增数列
6.(2024高三·全国·对口高考)设是公比为的等比数列,其前项的积为,并且满足条件:,,.给出下列结论:①;②;③;④使成立的最小的自然数n等于199.其中正确结论的编号是( )
A.①②③B.①④C.②③④D.①③④
7.(2024·广西·模拟预测)已知正项等比数列满足,则取最大值时的值为( )
A.8B.9C.10D.11
8.(2024高二上·广东清远·期中)已知数列满足,,则数列是( )
A.递增数列B.递减数列C.常数列D.不能确定
9.(2024高二上·陕西咸阳·期末)已知是递增的等比数列,且,则其公比满足( )
A.B.
C.D.
10.(2024高三上·江西赣州·期中)设公比为的等比数列的前项和为,前项积为,且,,,则下列结论正确的是( )
A.B.
C.是数列中的最大值D.数列无最大值
11.(2024高三上·贵州黔西·阶段练习)设等比数列的公比为,其前项和为,前项积为,且满足条件,,,则下列选项错误的是( )
A.B.
C.是数列中的最大项D.
12.(2024·上海青浦·一模)设等比数列的公比为,其前项之积为,并且满足条件:,,,给出下列结论:①;② ;③是数列中的最大项;④使成立的最大自然数等于4039;其中正确结论的序号为( )
A.①②B.①③C.①③④D.①②③④
13.(2024·全国)记为等比数列的前n项和,若,,则( ).
A.120B.85C.D.
14.(2024·天津)已知数列的前n项和为,若,则( )
A.16B.32C.54D.162
15.(2024·湖南长沙·二模)设等比数列的前项和为,已知,,则( )
A.B.C.D.
16.(2024高三下·陕西安康·阶段练习)在各项均为正数的等比数列中,,,则使得成立的n的最小值为( )
A.7B.8C.9D.10
17.(2024·四川巴中·模拟预测)在等比数列中,,,则( )
A.3B.6C.9D.18
18.(2024·河北沧州·模拟预测)已知公比不为1的等比数列满足,则( )
A.40B.81C.121D.156
19.(2024·河南·三模)数列{an}满足,,数列的前项积为,则( )
A.B.
C.D.
20.(2024·安徽安庆·三模)在等比数列中,,则( )
A.4B.8C.32D.64
21.(2024高三上·广西桂林·期末)已知各项都为正数的等比数列,满足,若存在两项,,使得,则最小值为( )
A.2B.C.D.1
二、多选题
22.(2024·山西大同·模拟预测)《庄子·天下》中有:“一尺之棰,日取其半,万世不竭”,其大意为:一根一尺长的木棰每天截取一半,永远都取不完,设第一天这根木棰截取一半后剩下尺,第二天截取剩下的一半后剩下尺,…,第五天截取剩下的一半后剩下尺,则下列说法正确的是( )
A.B.
C.D.
23.(2024·湖北武汉·三模)已知实数数列的前n项和为,下列说法正确的是( ).
A.若数列为等差数列,则恒成立
B.若数列为等差数列,则,,,…为等差数列
C.若数列为等比数列,且,,则
D.若数列为等比数列,则,,,…为等比数列
24.(2024·山东泰安·二模)若m,n是函数的两个不同零点,且m,n,这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则 .
25.(2024·江西新余·二模)已知数列中,,,且、是函数的两个零点,则 .
26.(2024高三·全国·课后作业)已知等比数列的公比,该数列前9项的乘积为1,则 .
27.(2024高二下·全国·课后作业)等比数列中,,,则公比q的值为 .
28.(2024高二下·北京·期中)在和之间插入三个数,使这五个数组成正项等比数列,则中间三个数的积等于 .
29.(2024高二下·湖北十堰·阶段练习)已知正项数列是公比不等于1的等比数列,且,若,则 .
30.(2024高三·重庆·阶段练习)在等比数列中,,,则
31.(2024高二·全国·课后作业)已知数列是等比数列,是其前项和,且,,则 .
32.(2024高三上·江苏泰州·期末)设正项等比数列的前项和为,若,则的值为 .
33.(2024高三上·重庆·阶段练习)已知等比数列的前项和为,,,则 .
34.(2024高二下·湖北十堰·阶段练习)已知正项等比数列的前项和为,若,,则,的等差中项为 .
35.(2024·江西南昌·模拟预测)已知等比数列的前项和为,若,,则的值为
36.(2024高三上·内蒙古包头·期末)已知数列和满足,,,.则数列的通项 .
37.(2024高三上·上海浦东新·开学考试)设幂函数,数列满足:,且(),则数列的通项 .
38.(2024高三·江苏·专题练习)写出一个满足前5项的和为31,且递减的等比数列的通项 .
39.(2024高二上·河南南阳·阶段练习)数列{an}的前n项和为Sn,a1=1,an+1=2Sn(n∈N*),则an= .
40.(2024高三上·内蒙古包头·期中)已知数列{}的通项与前n项和之间满足关系则=
41.(2024高一下·上海宝山·阶段练习)已知正数数列满足,且对恒成立,则的范围为 .
42.(2024·湖北武汉·模拟预测)已知等比数列的各项均为正数,公比为q,前n项和,若对于任意正整数n有,则q的范围为 .
43.(2003高一·北京·竞赛)若三角形三边成等比数列,则公比q的范围是 .
44.(2024·湖南长沙·三模)中国古代数学著作《增减算法统宗》中有这样一段记载:“三百七十八里关,初行健步不为难,次日脚痛减一半,如此六日过其关.” 则此人在第六天行走的路程是 里(用数字作答).
45.(2024·四川成都·三模)如图,已知在扇形OAB中,半径,,圆内切于扇形OAB(圆和,,弧AB均相切),作圆与圆,,相切,再作圆与圆,,相切,以此类推.设圆,圆…的面积依次为,…,那么 .
46.(2024·陕西西安·一模)“一尺之棰,日取其半,万世不竭”出自《庄子·天下》,其中蕴含着数列的相关知识,已知长度为4的线段,取的中点C,以为直径作圆(如图①),该圆的面积为,在图①中取的中点D,以为直径作圆(如图②),图②中所有圆的面积之和为,以此类推,则 .
47.(2024·贵州铜仁·二模)是无理数的近似值,被称为黄金比值.我们把腰与底的长度比为黄金比值的等腰三角形称为黄金三角形.如图,是顶角为,底的第一个黄金三角形,是顶角为的第二个黄金三角形,是顶角为的第三个黄金三角形,是顶角为的第四个黄金三角形,则第个黄金三角形的腰长为 (写出关于表达式即可).
四、解答题
48.(2024·安徽亳州·模拟预测)甲、乙、丙三个小学生相互抛沙包,第一次由甲抛出,每次抛出时,抛沙包者等可能的将沙包抛给另外两个人中的任何一个,设第()次抛沙包后沙包在甲手中的方法数为,在丙手中的方法数为.
(1)求证:数列为等比数列,并求出的通项;
(2)求证:当n为偶数时,.
49.(2024高三·上海·专题练习)已知数列是首项与公比都为的等比数列,其中,且,且是递增数列,求的范围.
50.(2024·江苏盐城·三模)已知数列、满足,,,,且,.
(1)求证:是等比数列;
(2)若是递增数列,求实数的取值范围.
51.(2024高三·全国·专题练习)数列的前和满足 ,
(1)求的值及与的关系;
(2)求证:是等比数列,并求出的通项公式.
52.(2024·云南·三模)已知数列有递推关系,,记,若数列的递推式形如(且),也即分子中不再含有常数项.
(1)求实数的值;
(2)证明:为等比数列,并求其首项和公比.
53.(2024·福建厦门·模拟预测)已知数列满足.
(1)证明是等比数列;
(2)若,求的前项和.
54.(2024·山东潍坊·三模)已知数列和满足.
(1)证明:和都是等比数列;
(2)求的前项和.
55.(2024高三·上海·专题练习)数列的通项的通项,由与中公共项,并按原顺序组成一个新的数列,求的前项和.
56.(2024·天津南开·二模)设为等比数列,为公差不为零的等差数列,且,,.
(1)求和的通项公式;
(2)记的前项和为,的前项和为,证明:;
(3)记,求.
57.(2024·湖南邵阳·三模)记为等差数列{}的前n项和,已知,数列{}满足.
(1)求数列{}与数列{}的通项公式;
(2)数列{}满足,n为偶数,求{}前2n项和.
58.(2024·山东菏泽·二模)已知各项为正数的等比数列满足.
(1)求数列的通项公式;
(2)设,,求数列的前2n项和.
59.(2024·浙江·二模)已知数列满足:,且对任意的,
(1)求,的值,并证明数列是等比数列;
(2)设,求数列的前项和.
60.(2024高三·全国·专题练习)已知数列满足,,记,求数列的通项公式.
61.(2024高三上·河北邢台·期末)已知数列为等差数列,,,前项和为,数列满足,求证:
(1)数列为等差数列;
(2)数列中任意三项均不能构成等比数列.
62.(2024高三上·浙江·期中)已知为等差数列的前项和,且,___________.在①,,成等比数列,②,③数列为等差数列,这三个条件中任选一个填入横线,使得条件完整,并解答:
(1)求;
(2)若,求数列的前项和.
注:如果选择多个条件分别解答,则按第一个解答计分.
63.(2024·四川资阳·一模)已知等比数列的前项和为,且,,(其中)成等差数列.问:,,是否成等差数列?并说明理由.
64.(2024高二下·湖北武汉·期末)已知是递增的等比数列,且,.
(1)求数列的通项公式;
(2)在与之间插入个数,使这个数组成一个公差为的等差数列,在数列中是否存在项(其中成等差数列)成等比数列.若存在,求出这样的项;若不存在,请说明理由.
65.(2024·福建福州·三模)设数列的前n项和为,,,.
(1)证明:为等差数列;
(2)设,在和之间插入n个数,使这个数构成公差为的等差数列,求的前n项和.
(一)
等比数列基本量的运算
等比数列基本量的运算的解题策略
(1)等比数列中有五个量a1,n,q,an,Sn,一般可以“知三求二”,通过列方程(组)可迎刃而解.
(2)解方程组时常常利用“作商”消元法.
(3)运用等比数列的前n项和公式时,一定要讨论公比q=1的情形,否则会漏解或增解.
题型1:等比数列基本量的运算
1-1.(2024高二下·全国·课后作业)在等比数列中,若,,则公比q应为( )
A.B.C.D.-2
1-2.(2024高三下·北京·阶段练习)在等比数列中,,,则等于( )
A.9B.72C.9或70D.9或
1-3.(2024高二下·湖北·阶段练习)已知递增的等比数列中,前3项的和为7,前3项的积为8,则的值为( )
A.2B.4C.6D.8
1-4.(2024高三·全国·对口高考)已知数列是等比数列,,则该数列的以及依次为( )
A.682,B.,C.682,或D.,或
1-5.(2024高三·全国·专题练习)已知等比数列中,,为前项和,,则( )
A.7B.9C.15D.30
(二)
等比数列的判定与证明
等比数列的三种常用判定方法
(1)定义法:若eq \f(an+1,an)=q(q为非零常数,n∈N*)或eq \f(an,an-1)=q(q为非零常数且n≥2,n∈N*),则{an}是等比数列.
(2)等比中项法:若数列{an}中,an≠0且aeq \\al(2,n+1)=an·an+2(n∈N*),则{an}是等比数列.
(3)前n项和公式法:若数列{an}的前n项和Sn=k·qn-k(k为常数且k≠0,q≠0,1),则{an}是等比数列.
题型2:等比数列的判定与证明
2-1.(2024高三·全国·专题练习)甲、乙两个容器中分别盛有浓度为10%,20%的某种溶液500ml,同时从甲、乙两个容器中取出100ml溶液,将其倒入对方的容器并搅匀,这称为一次调和.记,,经次调和后,甲、乙两个容器的溶液浓度分别为,.
(1)试用,表示,.
(2)证明:数列是等比数列,并求出,的通项.
2-2.(2024高三·全国·专题练习)已知数列满足,,其中为的前n项和.证明:
(1)是等比数列.
(2).
2-3.(2024·广东东莞·三模)已知数列和,,,.
(1)求证数列是等比数列;
(2)求数列的前项和.
(三)
等比数列项的性质
(1)等比数列的性质可以分为三类:一是通项公式的变形,二是等比中项的变形,三是前n项和公式的变形,根据题目条件,认真分析,发现具体的变化特征即可找出解决问题的突破口.
(2)巧用性质,减少运算量,在解题中非常重要.
题型3:等比数列项的性质
3-1.(2024·江西·二模)在正项等比数列中,与是方程 的两个根,则 .
3-2.(2024高三下·四川成都·阶段练习)若数列是等比数列,且,则 .
3-3.(2024·河南新乡·二模)已知等比数列的首项为,且,则 .
(四)
等比数列前n项和的性质
(1)等比数列中,所有奇数项之和与所有偶数项之和具有的性质,设公比为.
①若共有项,则;②若共有项,.
(2)等比数列中,表示它的前项和.当时,有也成等比数列,公比为.
题型4:等比数列前n项和的性质
4-1.(2024·河北沧州·模拟预测)已知等比数列的前项和为,若,,则 .
4-2.(2024高三·全国·对口高考)已知数列为等比数列,为其前n项和.若,,则的值为 .
4-3.(2024高三·全国·课后作业)已知是正项等比数列的前n项和,,则的最小值为 .
4-4.(2024·江苏南京·一模)设正项等比数列的前项和为,且,则公比 .
(五)
由求数列的通项
已知求是一种非常常见的题型,这些题都是由与前项和的关系来求数列的通项公式,可由数列的通项与前项和的关系是,注意:当时,若适合,则的情况可并入时的通项;当时,若不适合,则用分段函数的形式表示.
题型5:由求数列的通项
5-1.(2024高三·全国·对口高考)已知等比数列的前n项和为,则 .
5-2.(2024·广西玉林·三模)记数列的前n项和为,已知向量,,若,且,则通项为 .
5-3.(2024·全国·模拟预测)已知数列的前项和为且满足,则数列的通项 .
(六)
奇偶项求和问题的讨论
求解等比数列的前项和,要准确地记住求和公式,并合理选取公式,尤其是要注意其项数的值;对于奇偶项通项不统一问题要注意分类讨论.主要是从为奇数、偶数进行分类.
题型6:奇偶项求和问题的讨论
6-1.(2024高三·全国·对口高考)设数列的首项,且,
记.
(1)求;
(2)判断数列是否为等比数列,并证明你的结论;
(3)求.
6-2.(2024·湖南长沙·模拟预测)已知数列满足,且
(1)设,求数列的通项公式;
(2)设数列的前n项和为,求使得不等式成立的n的最小值.
6-3.(2024·河北·模拟预测)已知数列满足,
(1)记,证明:数列为等比数列;
(2)记,求数列的前项和.
6-4.(2024·山东济宁·二模)已知数列的前项和为,且.
(1)求数列的通项公式;
(2)若,求数列的前项和.
(七)
等差数列与等比数列的综合应用
(1)等差数列与等比数列的相互转化:等差数列通过指数运算转化为正项等比数列,正项等比数列通过对数运算转化为等差数列.
(2)等差数列和等比数列的交汇,若一个数列既是等差数列又是等比数列,则该数列为非零常数数列.
题型7:等差数列与等比数列的综合应用
7-1.(2024高二上·陕西渭南·期末)在等差数列中,.
(1)求等差数列的通项公式;
(2)设数列是首项为1,公比为2的等比数列,求数列的前项和.
7-2.(2024·江苏)已知是等差数列,是公比为q的等比数列,,,记为数列的前n项和.
(1)若(m,k是大于2正整数),求证:;
(2)若(i是某一正整数),求证:q是整数,且数列中每一项都是数列中的项;
(3)是否存在这样的正数q,使等比数列中有三项成等差数列?若存在,写出一个q的值,并加以说明;若不存在,请说明理由.
7-3.(2024高二上·福建龙岩·阶段练习)公差不为0的等差数列中,,且成等比数列.
(1)求数列的通项公式;
(2)若为等差数列的前项和,求使成立的的最大值.
(八)
等比数列的范围与最值问题
求解此类问题的常用思路是根据题目所给条件建立关于变量n的函数关系进行求解.有时也注意基本不等式的应用.
题型8:等比数列的范围与最值问题
8-1.(2024·陕西西安·三模)已知数列是无穷等比数列,若,则数列的前n项和( ).
A.无最大值,有最小值B.有最大值,有最小值
C.有最大值,无最小值D.无最大值,无最小值
8-2.(2024高三上·贵州铜仁·期末)已知等比数列的各项均为正数且公比大于1,前n项积为,且,则使得的n的最小值为( )
A.5B.6C.7D.8
8-3.(2024·北京海淀·模拟预测)设无穷等比数列的前项和为,若,则( )
A.为递减数列B.为递增数列
C.数列有最大项D.数列有最小项
8-4.(2024高三上·广西玉林·阶段练习)设等比数列的公比为q,其前n项和为,并且满足条件,则下列结论正确的是( )
A.B.C.D.的最大值为
8-5.(2024高三上·福建三明·期中)设等比数列的公比为,其前项和为,前项积为,并满足条件,,则下列结论正确的是( )
A.B.是数列中的最大值
C.D.数列无最大值
8-6.(2024·山东泰安·二模)已知数列的前n项和为,,,.
(1)求;
(2)设,数列的前n项和为,若,都有成立,求实数的范围.
(九)
等比数列的实际应用
(1)解应用问题的核心是建立数学模型.
(2)一般步骤:审题、抓住数量关系、建立数学模型.
(3)注意问题是求什么(n,an,Sn).
注:(1)解答数列应用题要注意步骤的规范性:设数列,判断数列,解题完毕要作答.
(2)在归纳或求通项公式时,一定要将项数n计算准确.
(3)在数列类型不易分辨时,要注意归纳递推关系.
(4)在近似计算时,要注意应用对数方法,且要看清题中对近似程度的要求.
题型9:等比数列的实际应用
9-1.(2024·广东广州·模拟预测)某牧场今年初牛的存栏数为1200,预计以后每年存栏数的增长率为,且在每年年底卖出100头牛.设牧场从今年起每年年初的计划存栏数依次为数列,且满足递推公式:为数列的前项和,则 (答案精确到1).
9-2.(2024·福建福州·三模)英国数学家亚历山大·艾利斯提出用音分来精确度量音程,音分是度量不同乐音频率比的单位,也可以称为度量音程的对数标度单位.一个八度音程为1200音分,它们的频率值构成一个等比数列.八度音程的冠音与根音的频率比为2,因此这1200个音的频率值构成一个公比为的等比数列.已知音M的频率为m,音分值为k,音N的频率为n,音分值为l.若,则=( )
A.400B.500C.600D.800
9-3.(2024·全国·三模)88键钢琴从左到右各键的音的频率组成一个递增的等比数列.若中音A(左起第49个键)的频率为,钢琴上最低音的频率为,则左起第61个键的音的频率为 .
9-4.(2024·辽宁大连·一模)某高中图书馆为毕业生提供网上阅读服务,其中电子阅览系统的登录码由学生的届别+班级+学号+特别码构成.这个特别码与如图数表有关,数表构成规律是:第一行数由正整数从小到大排列得到,下一行数由前一行每两个相邻数的和写在这两个数正中间下方得到.以此类推特别码是学生届别数对应表中相应行的自左向右第一个数的个位数字,如:1997届3班21号学生的登陆码为1997321*.(*为表中第1997行第一个数的个位数字).若已知某毕业生的登录码为201*2138,则可以推断该毕业生是 届2班13号学生.
专题40 圆的方程9题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测(原卷版): 这是一份专题40 圆的方程9题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测(原卷版),共16页。试卷主要包含了圆的定义和圆的方程,圆心在任一弦的垂直平分线上等内容,欢迎下载使用。
专题30 数列求和5题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测(原卷版): 这是一份专题30 数列求和5题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测(原卷版),共19页。试卷主要包含了公式法,分组求和法与并项求和法,错位相减法,裂项相消法等内容,欢迎下载使用。
专题29 求数列的通项公式10题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测(原卷版): 这是一份专题29 求数列的通项公式10题型分类-备战2025年高考数学一轮专题复习全套考点突破和专题检测(原卷版),共19页。试卷主要包含了数列的通项公式,数列的递推公式等内容,欢迎下载使用。












