22.1.3 第2课时 y=a(x-h)²的图象和性质-2024-2025学年九年级数学上册教材配套同步课件（人教版）

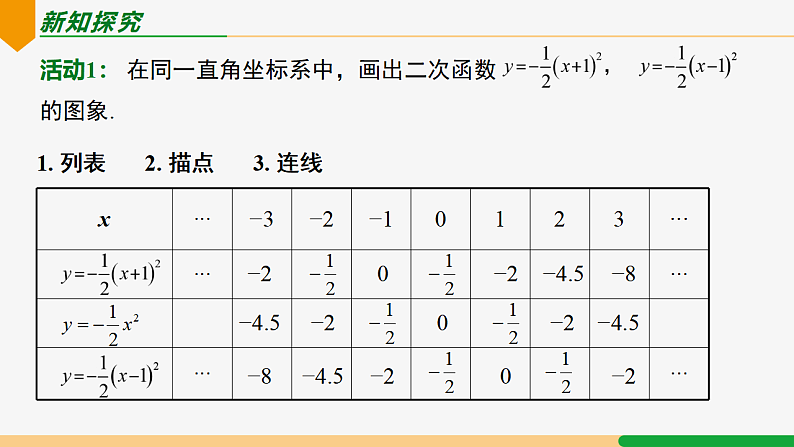
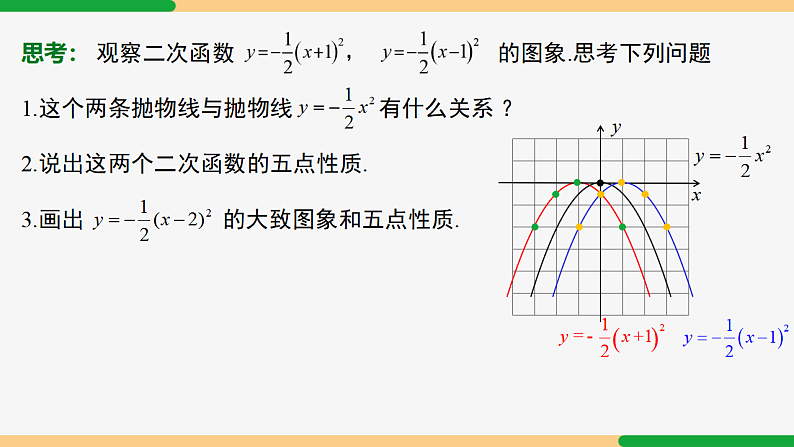
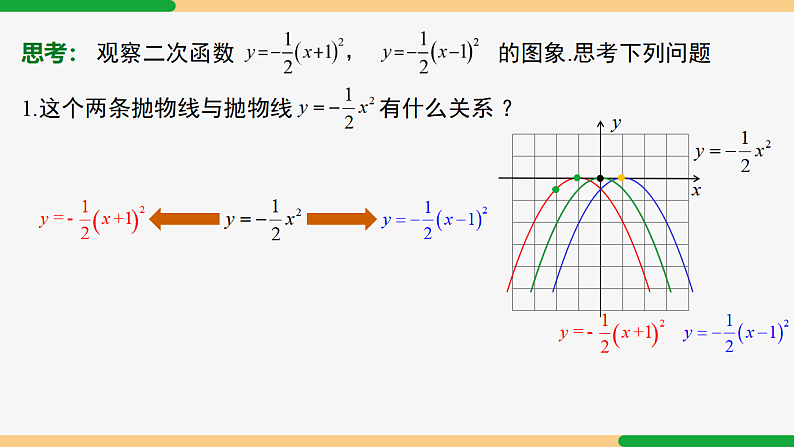
y= a(x − h)2的图象和性质22.1.3 二次函数y = a(x - h)2 + k的图象和性质| 第2课时|课堂导航二次函数y = a(x − h)2 的图象和性质二次函数y = a(x − h)2与y=ax²图象的关系 y = ax² + k a >0 知识回顾 图象y=kx+by=kx性质y=ax2+k类比y=ax2y = ax²y = ax² - k 平移规律上加下减知识要点2开口向上，a 越大，开口越小 y 轴(直线 x＝0)原点(0，k)当 x = 0 时，y最小值 = k当 x < 0 时，y 随 x 增大而减小；当 x > 0 时，y 随 x 增大而增大.开口向下，a 越大，开口越大y 轴(直线 x＝0)原点(0，k)当 x = 0 时，y最小值 =k当 x < 0 时，y 随 x 增大而减小；当 x > 0 时，y 随 x 增大而增大.新知探究活动1： 在同一直角坐标系中，画出二次函数 的图象.1. 列表2. 描点3. 连线−20−2−4.5−8−8−2−4.5−200−2−2−4.5−4.5xyxy知识要点1二次函数的图象的平移关系： 1.抛物线y =a(x-h)2 可以由抛物线y =ax2左右平移得到.y =a(x+h)2 y = ax²y =a(x-h)2 左右平移规律：自变量左加右减，括号外不变y =a(x+h)2 y = ax²y =a(x-h)2 当 h > 0思考： 观察二次函数 的图象.思考下列问题2.说出这两个二次函数的五点性质.xy1. 开口：2. 对称轴：3. 顶点 ：4. 最值：5. 增减性：开口向下；有高点 x= -1；x=1 (-1, 0)；(1, 0)；当 x = 1；-1 时，y最小值 =0 当 x＜-1 时，y 随 x 的增大而减大；当 x＞-1 时，y 随 x 的增大而增小.当 x＜1 时，y 随 x 的增大而减大； 当 x＞1 时，y 随 x 的增大而增小.思考： 观察二次函数 的图象.思考下列问题xy3.画出 的大致图象和五点性质.1. 开口：2. 对称轴：3. 顶点 ：4. 最值：5. 增减性：开口向下；有高点 x= 2 (2, 0)；当 x = 2时，y最小值 =0 当 x＜2时，y 随 x 的增大而减大；当 x＞2 时，y 随 x 的增大而增小.活动2： (1) 在同一直角坐标系中，画出二次函数 y = 2(x+2)² ， y =2(x-1)² 的图象.(2) 说出两个二次函数的性质.(3) 总结y = a(x-h)² 的图象与性质.xy = 2(x+2)² y = 2x² y = 2(x-1)² (-2, 0 )(1, 0 )知识要点2开口向上，a 越大，开口越小 x＝h原点(h，k)当 x = h 时，y最小值 =k当 x < h 时，y 随 x 增大而减小；当 x > h 时，y 随 x 增大而增大.开口向下，a 越大，开口越大x＝h原点(h，k)当 x = h 时，y最小值 =k当 x < h 时，y 随 x 增大而减小；当 x > h 时，y 随 x 增大而增大.针对练习1. 指出下列函数图象的开口方向，对称轴和顶点坐标.向上直线 x = 3(3，0)直线 x = 2直线 x = 1向下向上(2，0)(1，0)(1, 0 )典例讲解 (1) 画出大致图象，并写出该二次函数的图象的对称轴和顶点坐标；(2) 当 x 取何值时，y 随 x 的增大而增大？(3) 若 3≤x≤5，求 y 的取值范围；(4) 若抛物线上有两点 A(x1，y1)，B(x2，y2)，且 x1＜x2＜1，试比较 y1 与 y2 的大小．典例讲解 变式：1.若 −1≤x≤5，y 的取值范围是什么？解.∵当 −1≤x≤5 时，y 的最小值为 0，∴当−1≤x≤5时，y 的取值范围是 0≤y≤8.典例讲解 变式2：.若点 A(m，y1)，B(m + 1，y2) 在抛物线的图象上，且 m＞1，试比较 y1，y2 的大小，并说明理由．解：∵ m＞1，∴ 1＜m＜m + 1.∵ 当 x＞1 时，y 随 x 的增大而增大，∴ y1＜y2.例2 抛物线y＝ax2向右平移3个单位后经过点(－1，4)，求a的值和平移后的函数关系式．解：二次函数y＝ax2的图象向右平移3个单位后得：y＝a(x－3)2，把 x＝－1，y＝4代入，得4＝a(－1－3)2，解之得：∴平移后二次函数关系式为y＝ (x－3)2.针对练习2. 将二次函数 y＝－2x2 的图象平移后，可得到二次函数 y＝－2(x＋1)2 的图象，平移的方法是 (　　)A. 向上平移 1 个单位长度 B. 向下平移 1 个单位长度 C. 向左平移 1 个单位长度　 D. 向右平移 1 个单位长度C y=ax2 课堂小结图象性质y=ax2+ky=ax2上下平移开口方向对称轴顶点坐标最值增减性左右平移y=a(x-h)2h >0 y=a(x-h)2 y=a(x+h)2 知识要点2开口向上，a 越大，开口越小 x＝h原点(0，h)当 x = h 时，y最小值 = 0当 x < h 时，y 随 x 增大而减小；当 x > h 时，y 随 x 增大而增大.开口向下，a 越大，开口越大x＝h原点(0，h)当 x = h 时，y最小值 =0当 x < h 时，y 随 x 增大而减小；当 x > h 时，y 随 x 增大而增大.课堂练习1、抛物线y＝3(x-2)2可以由抛物线y＝3x2向 平移 个单位得到．2、二次函数y=-2(x-1)2的图象开口方向是 ，顶点坐标是 ，对称轴是 .3、要得到抛物线y= (x-4)2，可将抛物线y= x 2( ) A.向上平移4个单位 B.向下平移4个单位 C.向右平移4个单位 D.向左平移4个单位右2向下（1，0）x=1C4. 如果二次函数 y＝a(x﹣1)2 (a≠0) 的图象在它的对称轴右侧部分是上升的，那么 a 的取值范围是______． a＞05. 把抛物线 y = -x2 沿着 x 轴方向平移 3 个单位长度，那么平移后的抛物线解析式是 . y = -(x + 3)2 或 y = -(x - 3)2 y1 ＞y2 ＞ y3 x右下大5(5,0)直线 x=55< 5>5