




- 22.2 二次函数与一元二次方程 第2课时(求解)-2024-2025学年九年级数学上册教材配套同步课件(人教版) 课件 0 次下载
- 22.3 第1课时 几何图形的最大面积-2024-2025学年九年级数学上册教材配套同步课件(人教版) 课件 0 次下载
- 22.3 第3课时 抛物线形实物问题-2024-2025学年九年级数学上册教材配套同步课件(人教版) 课件 0 次下载
- 第22章 二次函数小结第1课时 知识结构与要点-2024-2025学年九年级数学上册教材配套同步课件(人教版) 课件 0 次下载
- 第22章 二次函数小结第2课时 专题一 二次函数的图象与性质-2024-2025学年九年级数学上册教材配套同步课件(人教版) 课件 0 次下载
初中数学22.3 实际问题与二次函数评课课件ppt
展开会求商品利润最大问题会找实际问题中的隐含条件
1. 二次函数 y = (x + 1)2 − 2 的最小值是( ) A.−2 B.−1 C.1 D.2
2. 二次函数 y = −2x2 − 4x + 3 (x≤−2) 的最大值为____.
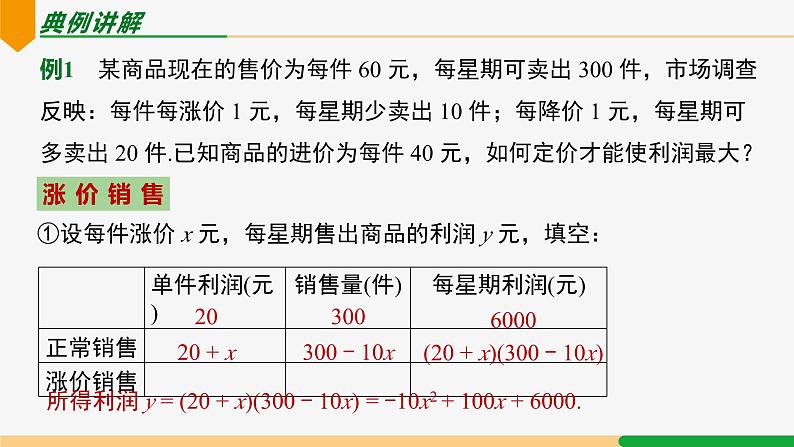
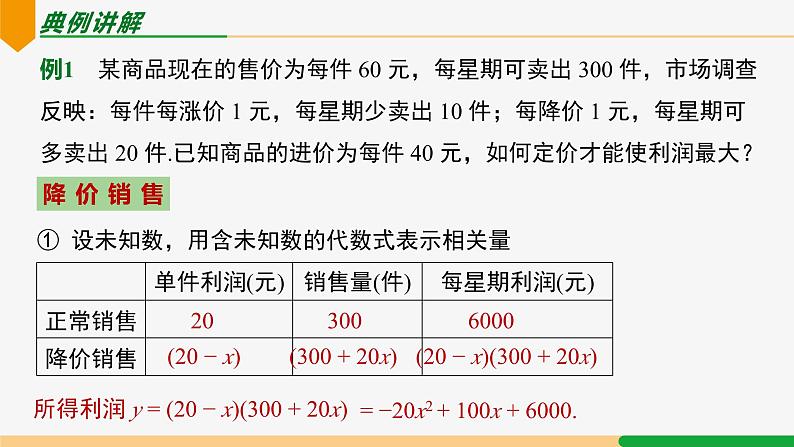
例1 某商品现在的售价为每件 60 元,每星期可卖出 300 件,市场调查反映:每件每涨价 1 元,每星期少卖出 10 件;每降价 1 元,每星期可多卖出 20 件.已知商品的进价为每件 40 元,如何定价才能使利润最大?
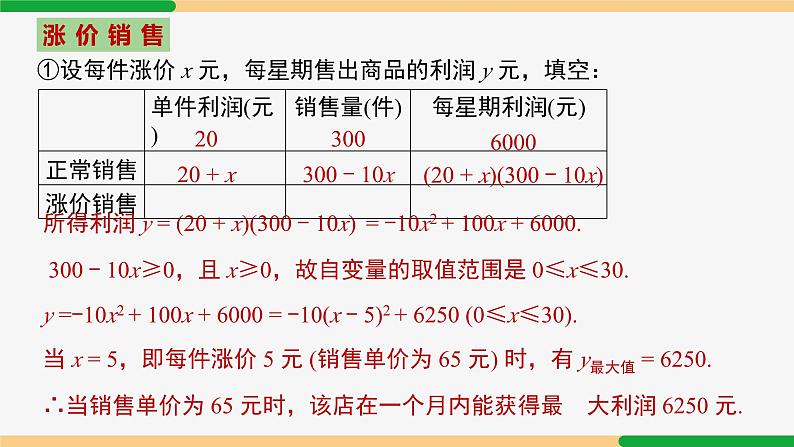
①设每件涨价 x 元,每星期售出商品的利润 y 元,填空:
(20 + x)(300 - 10x)
所得利润 y = (20 + x)(300 - 10x)
= -10x2 + 100x + 6000.
y =-10x2 + 100x + 6000 = -10(x - 5)2 + 6250 (0≤x≤30).
当 x = 5,即每件涨价 5 元 (销售单价为 65 元) 时,有 y最大值 = 6250.
∴当销售单价为 65 元时,该店在一个月内能获得最 大利润 6250 元.
300 - 10x≥0,且 x≥0,故自变量的取值范围是 0≤x≤30.
(300 + 20x)
(20 − x)(300 + 20x)
所得利润 y = (20 − x)(300 + 20x)
= −20x2 + 100x + 6000.
① 设未知数,用含未知数的代数式表示相关量
∵ 20 − x≥0,且 x≥0,∴ 0≤x≤20.
y = −20x2 + 100x + 6000
综上可知,定价为 65 元时,才有最大利润是 6250 元.
即每件降价 2.5 元时,利润最大,最大利润是 6125 元.
例2 某商店试销一种新商品,新商品的进价为 30 元/件,经过一段时间的试销发现,每月的销售量会因售价的调整而不同.令每月销售量为 y 件,售价为 x 元/件,每月的总利润为 Q 元.
(1) 当售价在 40~50 元/件时,每月销售量都为 60 件 则此时每月的总利润最多是多少元?
答:此时每月的总利润最多是1200元.
解:由题意知,当 40≤x≤50 时,
Q = 60(x − 30)
∵ y = 60 > 0,Q 随 x 的增大而增大,
∴ 当 x最大 = 50 时,Q最大 = 1200.
= 60x −1800.
(2) 当售价在 50~70 元/件时,每月销售量与售价的关系如图所示,则此时当该商品售价 x 是多少元/件时,该商店每月获利最大?最大利润是多少元?
解:当 50<x≤70 时,设 y 与 x 函数关系式为 y = kx + b,∵线段过 (50,60) 和 (70,20).
∴y = −2x + 160 (50<x≤70).
∴ Q = (x − 30)y = (x − 30)(−2x + 160) = −2x2 + 220x − 4800 = −2(x −55)2 +1250 (50<x≤70). ∵ a = −2<0,图象开口向下,∴ 当 x = 55 时,Q最大= 1250.∴ 当售价在 50~70 元/件时,售价 x 是 55 元时,获利 最大,最大利润是 1250 元.
总利润 = 单利润×总销量 总利润 = 总售价-总成本
涨价:要保证销售量≥0;降价:要保证单件利润≥0
利用配方法或公式求最大值或利用函数简图和性质求出
1. 一水果店售卖一种水果,以 8 元/千克的价格进货,经过往年销售经验可知:以 12 元/千克售 卖,每天可卖 60 千克:若每千克涨价 0.5 元,每天要少卖 2 千克;若每千克降价 0.5 元,每天要多卖 2 千克,但不低于成本价. 设该商品的价格为 x 元/千克时,一天销售总质量为 y 千克.(1) 求 y 与 x 的函数关系式.(2) 若水果店货源充足,每天以固定价格 x 元/千克销售 ( x > 8 ),试求出水果店每天利润 W 与单价 x 的函数关系式,并求出当 x 为何值时,利润达到最大.
解:(1) 由题意可得,
w = y(x − 8) = (−4x + 108)(x − 8) = −4x2 + 140x − 864
2. 一工艺师生产的某种产品按质量分为 9 个档次. 第 1 档次 (最低档次) 的产品一天能生产 80 件,每件可获利润 12 元. 产品每提高一个档次,每件产品的利润增加 2 元,但一天产量减少 4 件. 如果只从生产利润这一角度考虑,他生产哪个档次的产品,可获得最大利润?
解:设生产第x 档次的产品时,每天所获得的利润为 w 元, 则
w = [12 + 2(x-1)][80-4(x-1)] = (10 + 2x)(84-4x) = -8x2 + 128x + 840 = -8(x-8)2 + 1352.
因为 x ≤ 9,故当 x = 8 时,w 有最大值,且 w最大 = 1352.
答:该工艺师生产第 8 档次产品,可使利润最大,最大利润为 1352 元.
3. 某种商品每天的销售利润 y (元)与销售单价 x (元)之间满足关系:y = ax2 + bx - 75. 其图象如图.(1) 销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?(2) 销售单价在什么范围时,该种商品每天的销售利润不低于 16 元?
(2)解:由对称性知 y = 16 时,x = 7 或 13.故销售单价在 7≤x≤13 时,利润不低于 16 元.
(1) 解:由题中条件可求 y = -x2 + 20x - 75
∵-1 < 0,对称轴 x = 10,
∴当 x = 10 时,y 值最大,最大值为 25.即销售单价定为 10 元时,销售利润最大,为 25 元.
4. 某驻村扶贫小组实施产业扶贫,帮助贫困农户进行西瓜种植和销售. 已知西瓜的成本为 6 元/千克,规定销售单价不低于成本,又不高于成本的两倍. 经过市场调查发现,某天西瓜的销售量 y (千克)与销售单价 x (元/千克)的函数关系如图所示:
(1) 求 y 与 x 的函数解析式;(2) 求这一天销售西瓜获得的利润 W 的最大值.
解:(1) 当 6≤x≤10,设 y 与 x 的关系式为 y = kx + b (k≠0)
∴ y = -200x + 2200.
当 10≤x≤12,y = 200
故 y 与 x 的函数解析式为
初中数学人教版(2024)九年级上册22.3 实际问题与二次函数备课课件ppt: 这是一份初中数学人教版(2024)九年级上册<a href="/sx/tb_c95443_t3/?tag_id=26" target="_blank">22.3 实际问题与二次函数备课课件ppt</a>,共31页。PPT课件主要包含了复习回顾,2-7,新课导入,新知探究,数量关系,+20x,y最大值为6125元,-10n,巩固练习,方法小结等内容,欢迎下载使用。
人教版(2024)九年级上册第二十二章 二次函数22.3 实际问题与二次函数集体备课课件ppt: 这是一份人教版(2024)九年级上册<a href="/sx/tb_c95443_t3/?tag_id=26" target="_blank">第二十二章 二次函数22.3 实际问题与二次函数集体备课课件ppt</a>,共15页。PPT课件主要包含了300-10x,知识要点,30-x,20+x等内容,欢迎下载使用。
人教版九年级上册22.3 实际问题与二次函数教课ppt课件: 这是一份人教版九年级上册<a href="/sx/tb_c95443_t3/?tag_id=26" target="_blank">22.3 实际问题与二次函数教课ppt课件</a>,共20页。PPT课件主要包含了自主探究,小组讨论,小组展示,我提问,我回答,我补充,我质疑,越展越优秀,教师讲评等内容,欢迎下载使用。













