沪科版（2024）八年级上册14.2 三角形全等的判定课堂教学ppt课件

这是一份沪科版（2024）八年级上册14.2 三角形全等的判定课堂教学ppt课件，共18页。PPT课件主要包含了旧知回顾，∴AC＝DF，直角三角形全等的判定，画一画，4连接A′B′，几何语言，范例1，△ABC，△DCB，AAS等内容，欢迎下载使用。

答：共四种：SAS、ASA、SSS、AAS .
1.我们学过的证明一般三角形全等的方法有哪几种？
证明：在△ABC和△DEF中，
2.已知如右图所示，BC＝EF，AB⊥BE，垂足为B， DE⊥BE，垂足为E，AB＝DE.求证：AC＝DF.
将题中AB＝DE改成AC＝DF, 这两个三角形全等吗？
∴△ABC≌△DEF(SAS )，
任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A ′B ′C ′，使∠C′=90 °,B′C′=BC,A ′B ′=AB,把画好的Rt△A′B′ C′ 剪下来，放到Rt△ABC上，它们能重合吗？
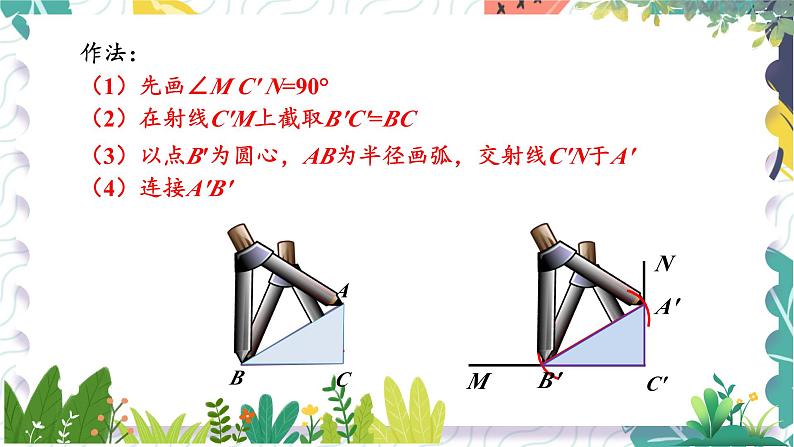
（1）先画∠M C′ N=90°
（2）在射线C′M上截取B′C′=BC
（3）以点B′为圆心，AB为半径画弧，交射线C′N于A′
“斜边、直角边”判定方法
斜边和一条直角边对应相等的两个直角三角形全等（简写成“斜边、直角边”或“HL”）.
在Rt△ABC和Rt△ A′B′C′ 中，
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
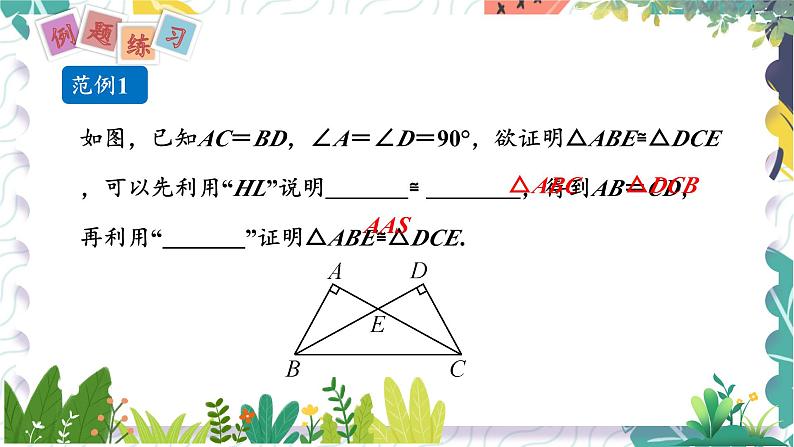
如图，已知AC＝BD，∠A＝∠D＝90°，欲证明△ABE≌△DCE，可以先利用“HL”说明 ≌ ，得到AB＝CD，再利用“ ”证明△ABE≌△DCE.
如图，BA∥DC，∠A＝90°，AB＝CE，BC＝ED，则△CED≌ ，AC＝ ，∠B＝ ．
如图，AD＝BC，AE＝CF，AE⊥BD于点E，CF⊥BD于点F. 求证：BE＝DF.
证明：∵AE⊥BD，CF⊥BD，∴∠AED＝∠CFB＝90°.在Rt△AED和Rt△CFB中， AD＝BC， AE＝CF，∴Rt△AED≌Rt△CFB (HL)，∴DE＝BF，∴DE＋EF＝BF＋EF，即DF＝BE.
HL的判定与三角形全等的判定的综合运用
证明： ∵∠BAC=∠CDB=90°，
在 Rt△BCD 和Rt△CBA中，
∴ Rt△BCD≌Rt△CBA (HL).
应用“HL”的前提条件是在直角三角形中.
这是应用“HL”判定方法的书写格式.
利用全等证明两条线段相等，这是常见的思路.
如图，∠BAC=∠CDB=90°， AC﹦DB，求证：AB﹦DC.
∴△BAC,△CDB都是直角三角形.
如图，AC⊥BC，AD⊥BD，AD＝BC，CE⊥AB，DF⊥AB，垂足分别是E、F，那么CE＝DF吗？
解：CE＝DF.∵AC⊥BC，AD⊥BD，∴∠ACB＝∠BDA＝90°，在Rt△ABC和Rt△BAD中， AD＝BC， AB＝BA，∴Rt△ABC≌Rt△BAD(HL)，∴∠CAE＝∠DBF，AC＝BD.∵CE⊥AB，DF⊥AB，∴∠AEC＝∠BFD＝90°，
在△AEC和△BFD中， ∠CAE＝∠DBF， ∠AEC＝∠BFD， AC＝BD，∴△AEC≌△BFD(AAS)∴CE＝DF.
如图，点D、A、E在直线MN上，AB＝AC，BD⊥MN于点D，CE⊥MN于点E，且BD＝AE.求证：DE＝BD＋EC.
证明：∵BD⊥MN，CE⊥MN，∴∠ADB＝∠AEC＝90°在Rt△ABD和Rt△CAE中， AB＝AC， BD＝AE，∴Rt△ABD≌Rt△CAE(HL)，∴AD＝CE，BD＝AE，∴DE＝EA＋AD＝BD＋EC.
如图①，点A、E、F、C在一条直线上，AE＝CF，过E、F分别作DE⊥AC，BF⊥AC，若AB＝CD.(1)求证：BD平分EF.(2)若将△DEC的边EC沿AC方向移动变为如图②所示时，其余条件不变，上述结论是否成立？请说明理由．
证明：(1)∵BF⊥AC，DE⊥AC，∴∠AFB＝∠DEC＝90°，∵AE＝CF，∴AE＋EF＝CF＋EF, 即AF＝CE，在Rt△ABF和Rt△CDE中， AB＝CD， AF＝CE，∴Rt△ABF≌Rt△CDE(HL)，∴BF＝DE.
在△BFG和△DEG中，
∠BGF＝∠DGE，∠BFG＝∠DEG， BF＝DE，
∴△BFG≌△DEG(AAS)∴FG＝EG，∴BD平分EF.
(2)仍然成立．理由：∵AE＝CF，∴AE－EF＝CF－EF，即AF＝CE，由HL知Rt△AFB≌Rt△CED，∴BF＝DE，由于∠BFG＝∠DEG＝90°， ∠BGF＝∠DGE，∴△BFG≌△DEG(AAS)，∴FG＝EG，∴BD平分EF .
已知：如图，AC⊥BD于点O，且OA=OC，AB=CD. 求证：AB//DC.
证明：∵ AC⊥BD于点O，
∴∠AOB=∠DOC=90°
△AOB和△COD都是直角三角形
∵ OA=OC，AB=CD.
2.如图，在△ABC中，已知BD⊥AC，CE ⊥AB，BD=CE.求证：△EBC≌△DCB.
证明： ∵ BD⊥AC，CE⊥AB， ∴∠BEC=∠BDC=90 °.
在 Rt△EBC 和Rt△DCB 中，
∴ Rt△EBC≌Rt△DCB (HL).
3.如图，AB=CD ，BF⊥AC ，DE⊥AC ，AE=CF. 求证：BF=DE.
证明: ∵ BF⊥AC,DE⊥AC,
∴ Rt△ABF≌Rt△CDE(HL).
∴∠BFA=∠DEC=90 °.
∴AE+EF=CF+EF.
在Rt△ABF和Rt△CDE中，
斜边和一条直角边对应相等的两个直角三角形全等.
只须找除直角外的两个条件即可（两个条件中至少有一个条件是一对对应边相等）