初中数学沪科版（2024）八年级上册15.3 等腰三角形课文配套课件ppt

这是一份初中数学沪科版（2024）八年级上册15.3 等腰三角形课文配套课件ppt，共18页。PPT课件主要包含了旧知回顾，典例1，典例2，仿例1，仿例2，变式训练等内容，欢迎下载使用。

1．进一步认识等腰三角形的定义和性质；2．通过观察、操作、想象、推理和交流活动，理解等腰三角形“三线合一”等有关性质，提高几何推理意识．
【学习重点】掌握等腰三角形的性质．
【学习难点】对等腰三角形“三线合一”的理解．
答：有两边相等的三角形是等腰三角形；
1．什么是等腰三角形？指出等腰三角形边、角的名称．
等腰三角形边、角名称如右图所示，相等的两边叫做腰，两腰夹角为顶角，腰和底的夹角为底角．
知识模块一　等腰三角形性质定理1
等腰三角形性质定理1的内容是什么？如何证明？
阅读教材P132的内容，回答下列问题：
答：等腰三角形的两底角相等， 简称“等边对等角”．
证明如图：已知在△ABC中，AB＝AC，求证：∠B＝∠C.
证明：过A作AD⊥BC于D，∵AB＝AC，AD＝AD，∴Rt△ABD≌Rt△ACD(HL)，∴∠B＝∠C.
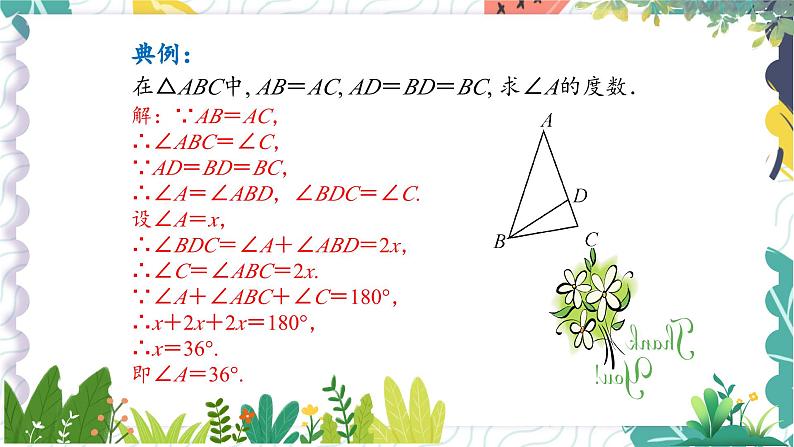
在△ABC中, AB＝AC, AD＝BD＝BC, 求∠A的度数．
解：∵AB＝AC，∴∠ABC＝∠C，∵AD＝BD＝BC，∴∠A＝∠ABD，∠BDC＝∠C.设∠A＝x，∴∠BDC＝∠A＋∠ABD＝2x，∴∠C＝∠ABC＝2x.∵∠A＋∠ABC＋∠C＝180°，∴x＋2x＋2x＝180°，∴x＝36°.即∠A＝36°.
如图，在△ABC中，点D在BC上，AB＝AD＝DC，∠B＝80°，则∠C的度数为 (　 　) A．30°　 B．40°　 C．45°　 D．60°
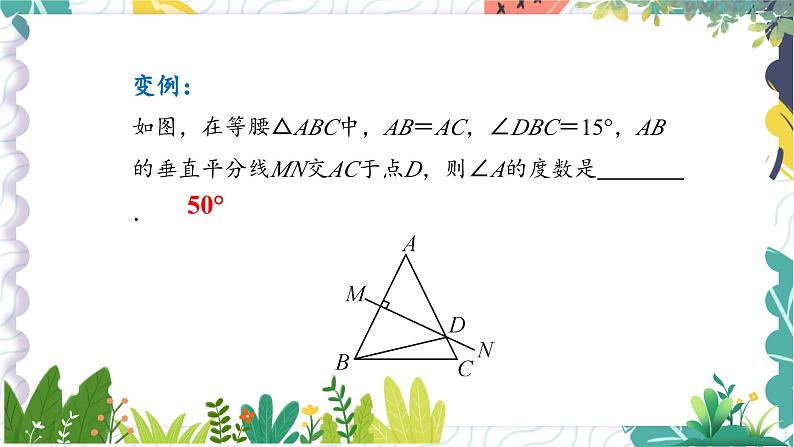
如图，在等腰△ABC中，AB＝AC，∠DBC＝15°，AB的垂直平分线MN交AC于点D，则∠A的度数是 ．
知识模块二 等腰三角形性质定理2与等边三角形的性质
1．等腰三角形性质定理2的内容是什么？ 如何用几何语言表示？
阅读教材P133的内容，回答下列问题：
答：等腰三角形顶角平分线垂直平分底边
即等腰三角形顶角平分线、底边上中线和底边上的高三线合一．
如图．当AB＝AC，AD⊥BC时⇒BD＝CD，∠BAD＝∠CAD；当AB＝AC，BD＝CD时⇒AD⊥BC，∠BAD＝∠CAD；当AB＝AC，∠BAD＝∠CAD时⇒AD⊥BC，BD＝CD.
2．等边三角形的性质是什么？
答：等边三角形三个内角相等， 每一个内角都等于60°.
如图，在△ABC中，AB＝AC，BC＝6，AD⊥BC于D，则BD＝ ．
如图，在△ABC中，AB＝AC，点D为BC边的中点，若∠BAD＝20°，则∠C＝ ．
在△ABC中，AB＝AC，AD为顶角∠BAC的平分线，若AD＝4cm，△ABC的周长为16cm，则△ABD的周长是 ．
如图，等边△ABC中，BE和CD分别是AC和AB边上的高，且相交于点F，则∠BFC＝ ．
如图，已知AB＝AC，D、E为线段BC上的点，且有AD＝AE，求证：BD＝CE.
证明：本题证明可用两种方法．方法一：过A作AH⊥BC于H，∵AB＝AC，AH⊥BC， 由三线合一得BH＝CH，∵AD＝AE，AH⊥DE， 由三线合一得DH＝EH，∴BH－DH＝CH－EH， 即BD＝CE.
方法二：不加辅助线，讨论完成．
本节课你学习了哪些知识？
学习了等腰三角形的有关性质
1.如图，△ABC是等边三角形，E是AC上一点，D是BC延长线上一点，连接BE，DE，若∠ABE＝40°，BE＝DE，求∠CED的度数．
解：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝60°.∵∠ABE＝40°，∴∠EBC＝∠ABC－∠ABE＝60°－40°＝20°.∵BE＝DE， ∴∠D＝∠EBC＝20°，∴∠CED＝∠ACB－∠D＝40°.
方法总结：等边三角形是特殊的三角形，它的三个内角都是60°，这个性质常应用在求三角形角度的问题上，一般需结合”等边对等角”、三角形的内角和与外角的性质.
如图，△ABC是等边三角形，BD平分∠ABC，延长BC到E，使得CE=CD．求证：BD=DE．
证明：∵△ABC是等边三角形，BD是角平分线，∴∠ABC=∠ACB=60°．∠DBC=30°（等腰三角形三线合一）．又∵CE=CD，∴∠CDE=∠CED．又∵∠BCD=∠CDE+∠CED，∴∠CDE=∠CED=30°．∴∠DBC=∠DEC．∴DB=DE（等角对等边）．