



数学沪科版(2024)15.3 等腰三角形课前预习ppt课件
展开1.复习巩固等腰三角形相关性质;2.熟练应用等腰三角形性质解答问题.
【学习重点】等腰三角形性质定理的应用.
【学习难点】等腰三角形性质定理的应用.
性质1:等腰三角形两个底角相等,简称“等边对等角”.
1.等腰三角形性质定理1是什么?
性质2:等腰三角形顶角的平分线垂直平分底边.
2.等腰三角形定理2是什么?等边三角形性质是什么?
等腰三角形顶角的平分线、底边上的中线和底边上的高三线合一.
推论:等边三角形三个内角相等,每个内角都等于60°
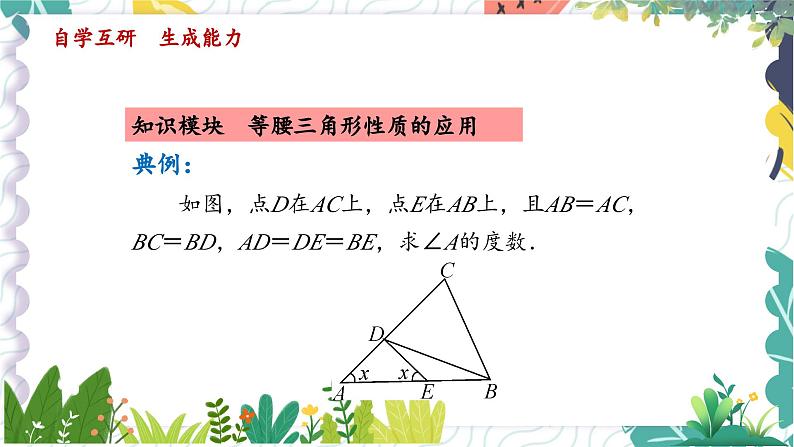
知识模块 等腰三角形性质的应用
如图,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=BE,求∠A的度数.
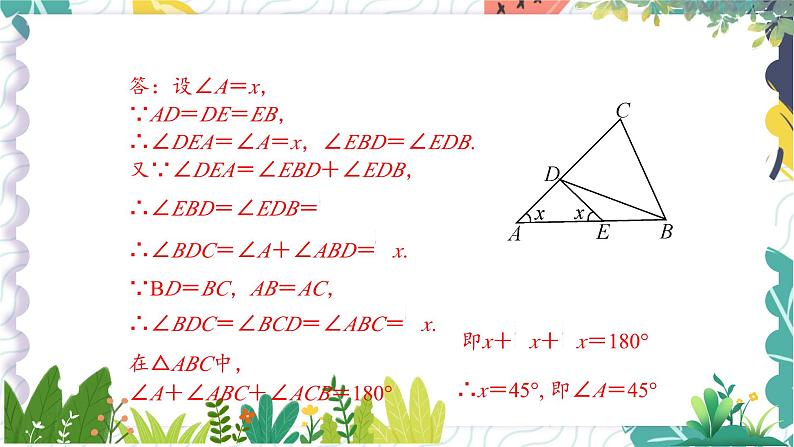
答:设∠A=x,∵AD=DE=EB,∴∠DEA=∠A=x,∠EBD=∠EDB.又∵∠DEA=∠EBD+∠EDB,
∵BD=BC,AB=AC,
在△ABC中,∠A+∠ABC+∠ACB=180°
∴x=45°, 即∠A=45°
如图,∠A=15°,AB=BC=CD=DE=EF=FG,求∠EFG的度数.
解:由AB=BC,∠A=∠ACB=15°,∴∠DBC=30°.∵CB=CD,∴∠DBC=∠BDC=30°,∴∠DCE=45°,依次类推,可得∠EFG=30°.
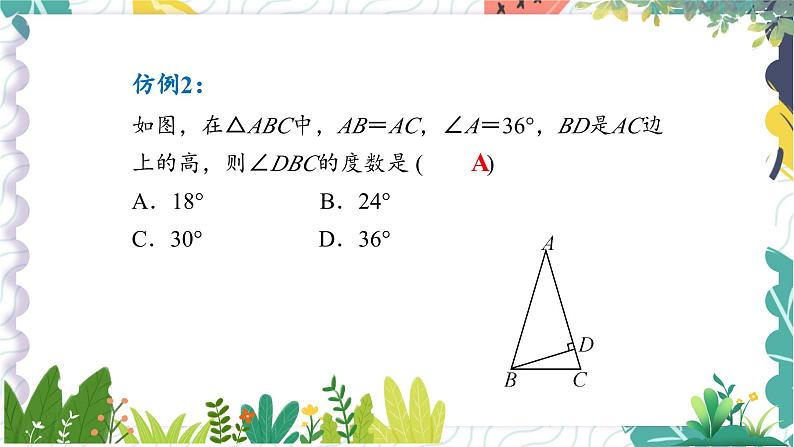
如图,在△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是 ( ) A.18° B.24° C.30° D.36°
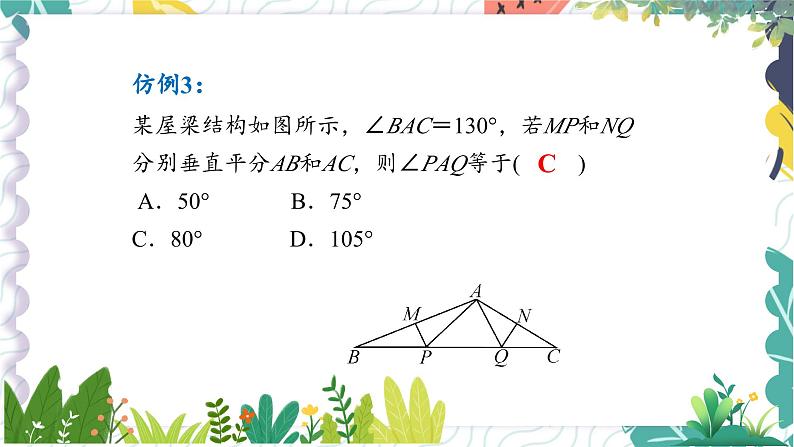
某屋梁结构如图所示,∠BAC=130°,若MP和NQ分别垂直平分AB和AC,则∠PAQ等于( ) A.50° B.75° C.80° D.105°
如图,△ABC是等边三角形,AD⊥BC,AE=AD,则∠ADE= .
等腰三角形一腰上的高与另一腰的夹角为36°,则该等腰三角形的底角的度数为 .
如图,△ABC为等边三角形,P为BC上一点,△APQ为等边三角形.(1)求证:AB∥CQ;(2)AQ与CQ能否互相垂直?若能互相垂直,指出点P在BC上的位置,并证明,若AQ与CQ不垂直,说明理由.
解:(1)∵△ABC,△APQ是等边三角形,∴AB=AC,∠BAC=∠PAQ=60°,AP=AQ,∴∠BAC-∠PAC=∠PAQ-∠PAC, 即∠BAP=∠CAQ,∴△ABP≌△ACQ(SAS),∴∠ACQ=∠B=60°. 又∵∠BAC=60°,∴∠ACQ=∠BAC,∴AB∥CQ.
(2)当点P在BC中点处时,AQ⊥CQ.∵△ABC是等边三角形,BP=CP,∴AP⊥BC,∴∠APB=90°.∵△ABP≌△ACQ,∴∠AQC=∠APB=90°,∴AQ⊥CQ.
本节课你学习了哪些知识?
利用等腰三角形的性质解决一些实际问题。
证明:∵△ABC 是等边三角形, ∴∠A =∠ABC =∠ACB =60°. ∵DE∥BC, ∴∠ABC =∠ADE, ∠ACB =∠AED. ∴∠A =∠ADE =∠AED. ∴△ADE 是等边三角形.
1.若点D、E 在边AB、AC 的延长线上,且DE∥BC,结论还成立吗?
2.若点D、E 在边AB、AC 的反向延长线上,且DE∥BC,结论依然成立吗?
证明: ∵△ABC 是等边三角形,∴∠BAC =∠B =∠C =60°.∵DE∥BC,∴∠B =∠D,∠C =∠E.∴∠EAD =∠D =∠E.∴△ADE 是等边三角形.
3.上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗?试说明理由.
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
初中数学沪科版(2024)八年级上册15.3 等腰三角形背景图课件ppt: 这是一份初中数学沪科版(2024)八年级上册15.3 等腰三角形背景图课件ppt,共24页。PPT课件主要包含了学习目标,情景导入生成问题,旧知回顾,自学互研生成能力,仿例1,等腰三角形,仿例2,仿例3,典例1,典例2等内容,欢迎下载使用。
初中数学沪科版(2024)八年级上册15.3 等腰三角形课文配套课件ppt: 这是一份初中数学沪科版(2024)八年级上册15.3 等腰三角形课文配套课件ppt,共18页。PPT课件主要包含了旧知回顾,典例1,典例2,仿例1,仿例2,变式训练等内容,欢迎下载使用。
初中数学沪科版(2024)八年级上册第15章 轴对称图形和等腰三角形15.1 轴对称图形课前预习课件ppt: 这是一份初中数学沪科版(2024)八年级上册第15章 轴对称图形和等腰三角形15.1 轴对称图形课前预习课件ppt,共18页。PPT课件主要包含了旧知回顾,对称点,对称轴,轴对称,观察规律填空等内容,欢迎下载使用。













