初中数学苏科版（2024）九年级上册3.2 中位数与众数完美版课件ppt

这是一份初中数学苏科版（2024）九年级上册3.2 中位数与众数完美版课件ppt，共26页。PPT课件主要包含了学习目标，唯一一定存在，平均数是4，众数是3，中位数是3，只与中间数据有关，中位数与众数，中位数与众数的概念，整理数据，分析数据等内容，欢迎下载使用。

2.能根据实际问题求出一组数据的中位数和众数.
1.理解中位数、众数的概念和意义;
问题1 在“献爱心”捐款活动中，某校九年级(1)班第3小组11名同学的捐款数如下（单位：元）：4，4，2，3，3，5，7，6，8，10，80.(1)求出这组数据的平均数；
(2)你认为“12”能较好地反映该组同学捐款数的“集中趋势”吗？
(2)这个小组11名同学中，捐款数高于12元的只有1人，低于12元的有10人.数据“12”不能很好地反映该组同学捐款的“集中趋势”.
像这样的一组数据的集中趋势怎样来描述呢？
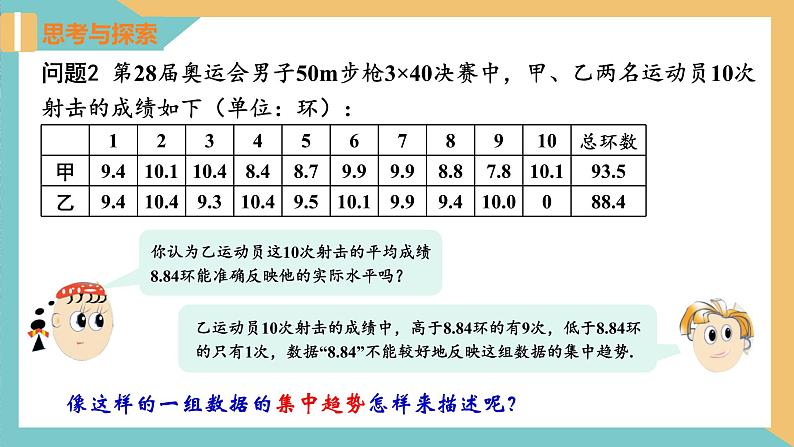
问题2 第28届奥运会男子50m步枪3×40决赛中，甲、乙两名运动员10次射击的成绩如下（单位：环）：
4，4，2，3，3，5，7，6，8，10，80.
2，3，3，4，4，5，6，7，8，10，80.
将“问题1”中11名同学的捐款数按从小到大的顺序排列，你有什么发现？
将“问题2”中乙运动员10次射击的环数按从小到大的顺序排列，你有什么发现？
9.4，10.4，9.3，10.4，9.5，10.1，9.9，9.4，10.0，0
0，9.3，9.4，9.4，9.5，9.9，10.0，10.1，10.4，10.4.
5和9.7能反映这两组数据的集中趋势吗？
一般地，将一组数据按大小顺序排列,如果数据的个数是奇数,那么处于中间位置的数叫做这组数据的中位数;如果数据的个数是偶数,那么处于中间位置的两个数的平均数叫做这组数据的中位数.
“问题1”中数据的中位数是5；“问题2”中数据的中位数是9.7.
当一组数据中个别数据与其他数据的大小差异很大时，通常用中位数来描述这组数据的集中趋势.可以不受个别变动较大的数据的影响.
2. 已知一组数据：65，60，70，80，75，85，这组数据从小到大排列为______________________，所以中位数为(____＋____)÷2＝_____．
1. 已知一组数据：-1，3，1，-2，3这组数据从小到大排列为____________________，中位数____．
-2，-1，1，3，3
60，65，70，75，80，85
3. 某市在一次空气污染指数抽查中，收集到10天的数据如下：106，60，74，100，92，67，75，67，87，119.该组数据的中位数是________．
求一组数据的中位数步骤：
1.将一组数据按照大小顺序排列；
2.当数据的个数是奇数时，则处于中间位置的一个数是这组数据的中位数;
当数据的个数是偶数时，则处于中间位置的两个数椐的平均数就是这组数据的中位数;
中位数也是用来描述数据的集中趋势的，它是一个位置代表值. 如果知道一组数据的中位数，那么可以知道，不大于或不小于这个中位数的数据约各占一半.
中位数不一定与这组数据中的某个数据相同.
问题3 小明在校内抽样调查了30名男同学的衬衣尺码，数据如下(单位：cm)：
你认为学校商店应多采购哪种尺码的男衬衫？说说你的理由.
问题4 某鞋店在一段时间内销售了某种运动鞋120双，其中各种尺码的鞋销售量如下表：
你认为，在这个问题中，鞋店比较关心的是什么？说说你的想法.
“问题3”中，数据“39”出现的次数最多，“39”是这组数据的众数；
一组数据中出现次数最多的数据叫做这组数据的众数.
“问题4”中，数据“40”出现的次数最多，“30”是这组数据的众数；
当一组数据中有较多的重复数据时，常用众数来描述这组数据的集中趋势.
1. 数据1，2，3，4，4，5的众数是______.
2. 一名射击运动员在一次射击练习中打出的成绩如下表所示：
这次成绩的众数是____环．
3. 在体育测试中，7名女生仰卧起坐的成绩如下（单位：次/分）：38、42、42、45、42、45、45.这组数据的众数是_________.
一组数据的众数不一定是唯一的，可以有不止一个众数.
例 为了解居民用水情况，小丽在自家居住的小区随机抽查了10户家庭月用水量，统计如下表：
则这10户家庭的月用水量的众数为 　9　⁠m3，中位数为 　8.5　⁠m3.
1.对于数据组：3，3，2，3，6，3，10，3，6，3，2①这组数据的众数是3；②这组数据的众数与中位数的数值不等；③这组数据的中位数与平均数的数值相等；④这组数据的平均数与众数的数值相等.其中正确的结论有( ) A. 1个 B. 2个 C. 3个 D. 4个
2，2，3，3，3，3，3，3，6，6，10
2. 某校九年级8个班级向“希望工程”捐献图书，捐书情况如下：
（1）求平均每个班级所捐图书的册数.（2）求所捐图书的册数的中位数和众数．
答:（1）平均每个班级捐书142册；
（2）捐书册数的中位数是93册，众数是90册.
3. 某射击小组有20人，某次射击的成绩如下：
（1）求该小组这次射击的平均成绩；（2）求这组数据的中位数和众数.
答:（1）7.55环；（2）中位数7.5，众数7.
中位数、众数、平均数的联系与区别：
反映一组数据的“集中趋势”
充分利用所有数据的信息，反映这组数据的平均水平
易受个别数据的影响，有时会与实际情况偏差较大
不受个别特殊数据的影响，反映一组数据的中间水平
不受个别特殊数据的影响，反映一组数据的多数水平
只与个数最多的数据有关
中位数、众数、平均数的联系与区别
1. 为了资金的迅速周转和减少商品库存积压,某手机销售商在进货时要关注各品牌手机销量的 ( ) A. 众数 　 B. 中位数 C. 平均数 　　　 D. 都不是
2. 文艺演出一般由若干名评委对节目打分，评选优秀节目的依据是 ( ) A. 众数 B. 中位数 C. 平均数 D. 都不是
3. 为了考察某同学在一次测验中数学成绩是占上等还是占下等水平，应关注这次数学成绩的 ( ) A. 众数 B. 中位数 C. 平均数 D. 都不是
5. 若一组数据1、x、2、4、5、4的众数为4和5，则这组数据的中位数是( )
4. 某公司对25名营销人员4月销售某种商品的情况统计如下表：
则这25名营销人员销售量的众数是 ( )
A. 50件 B. 40件 C. 35件 D. 30件
A. 2 B. 3 C. 4 D. 5
6.某家电商场三、四月份出售同一种品牌各种规格的空调，销售台数如下表，根据下表回答问题：(1)商场平均每月销售空调_____台．(2)商场出售的各种规格的空调中，众数落在________规格内．(3)在研究六月份的进货方案时，你认为________规格的空调要多进，________规格的空调要少进．
7. 为了加强对青少年防溺水安全教育，5月底某校开展了“远离溺水，珍爱生命”的防溺水安全知识比赛.下面是从参赛学生中随机收集到的20名学生的成绩（单位：分）：87、99、86、89、91、91、95、96、87、97、91、97、96、86、96、89、100、91、99、97.
(1)直接写出上面表格中的a、b、c、d的值；
解:（1） a＝4，b＝3，c＝91，d＝93　
(2)若成绩达到95分及以上为“优秀”等级，求“优秀”等级所占的百分率；
(3)请估计该校1500名学生中成绩达到95分及以上的学生人数.
解:（3） 估计该校1500名学生中成绩达到95分及以上的学生人数为1500×50%＝750
8.甲、乙两县参加由地区教育局举办的“双语口语”大赛，两县参赛人数相等.比赛结束后，学生成绩分别为7分、8分、9分、10分(满分10分).甲、乙两县不完整成绩统计情况如下表，乙县成绩情况如图所示.