沪科版（2024）八年级上册15.1 轴对称图形完美版ppt课件

这是一份沪科版（2024）八年级上册15.1 轴对称图形完美版ppt课件，共27页。PPT课件主要包含了本节课你有什么收获等内容，欢迎下载使用。

如果一个平面图形沿着一条直线折叠，直线两旁的部分能够完全重合，那么这个图形叫做轴对称图形，这条直线叫做对称轴.

平面内两个图形在一条直线的两旁，如果沿着这条直线折叠，这两个图形能够重合，那么称这两个图形关于这条直线成 轴对称.这条直线叫做 对称轴.折叠后重合的两点叫 对应点(也叫对称点) .
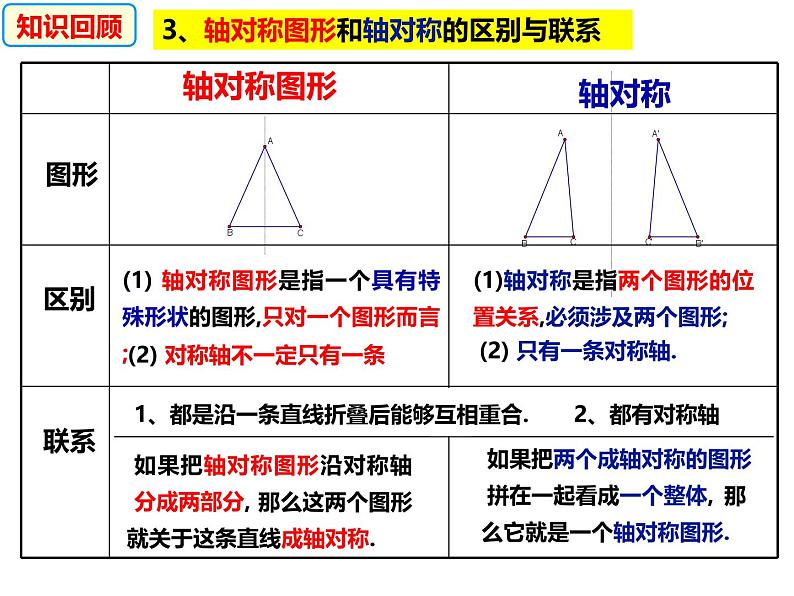
3、轴对称图形和轴对称的区别与联系
(1) 轴对称图形是指一个具有特殊形状的图形,只对一个图形而言;
如果把轴对称图形沿对称轴分成两部分,
(2) 对称轴不一定只有一条
(1)轴对称是指两个图形的位置关系,必须涉及两个图形;
如果把两个成轴对称的图形 拼在一起看成一个整体,
(2) 只有一条对称轴.
1、都是沿一条直线折叠后能够互相重合.
那么这两个图形 就关于这条直线成轴对称.
那么它就是一个轴对称图形.
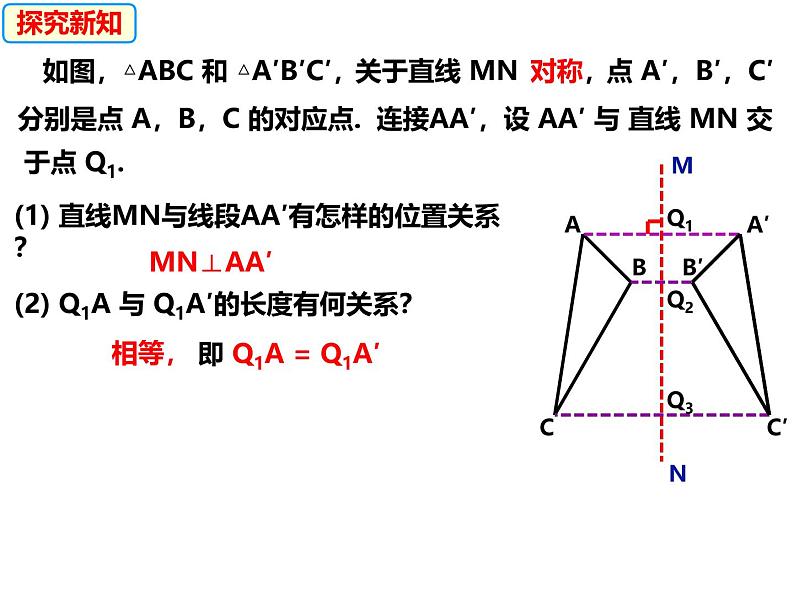
如图，△ABC 和 △A′B′C′，
分别是点 A，B，C 的对应点.
连接AA′，设 AA′ 与 直线 MN 交
(1) 直线MN与线段AA′有怎样的位置关系？
(2) Q1A 与 Q1A′的长度有何关系？
即 Q1A = Q1A′
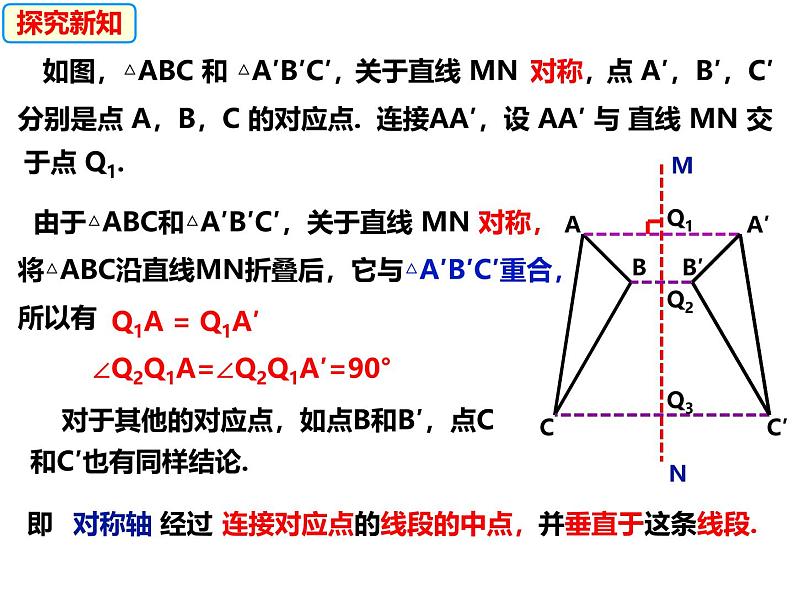
由于△ABC和△A′B′C′，关于直线 MN 对称，将△ABC沿直线MN折叠后，它与△A′B′C′重合，所以有
Q1A = Q1A′
∠Q2Q1A=∠Q2Q1A′=90°
对于其他的对应点，如点B和B′，点C和C′也有同样结论.
连接对应点的线段的中点，
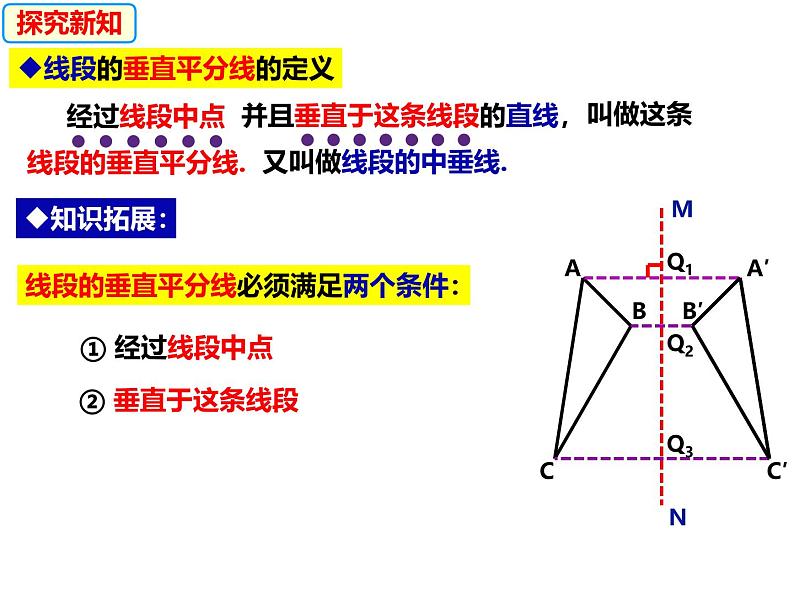
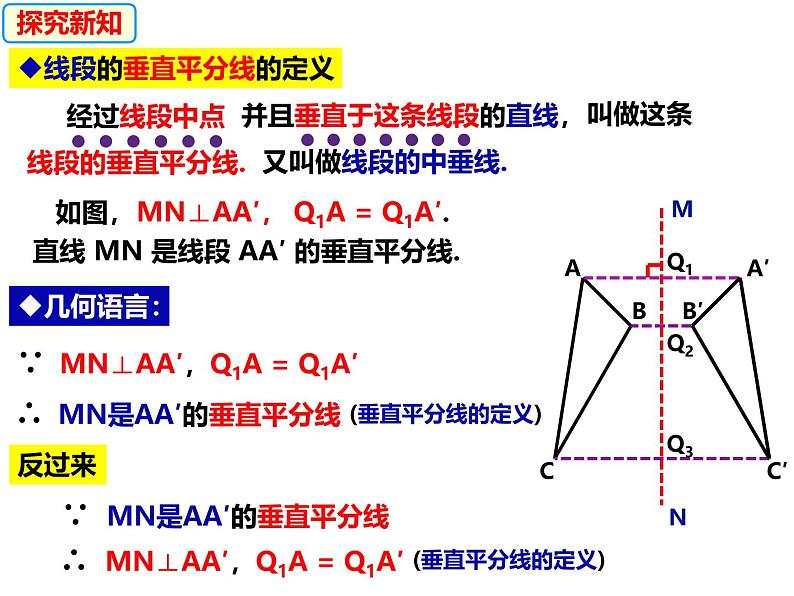
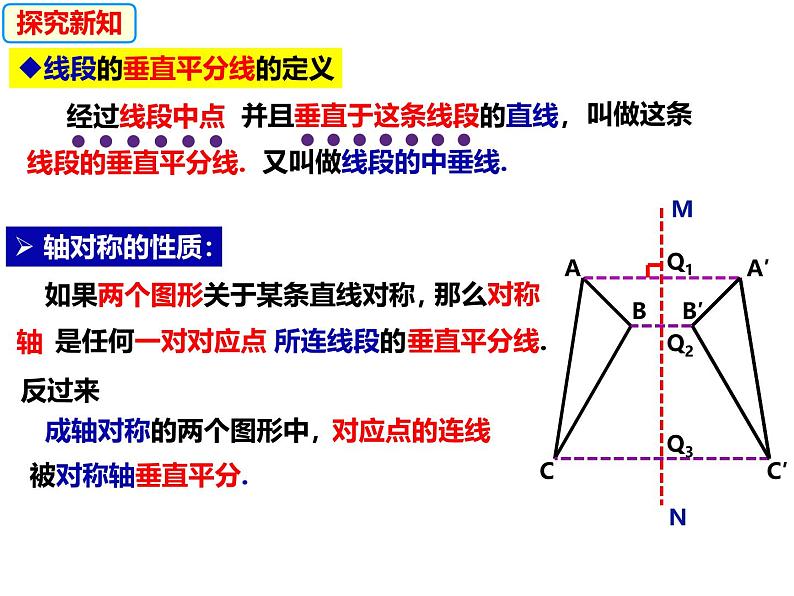
线段的垂直平分线的定义
并且垂直于这条线段的直线，
线段的垂直平分线必须满足两个条件：
Q1A = Q1A′.
直线 MN 是线段 AA′ 的垂直平分线.
∴ MN是AA′的垂直平分线
∵ MN⊥AA′，Q1A = Q1A′
∵ MN是AA′的垂直平分线
∴ MN⊥AA′，Q1A = Q1A′
那么对称轴
如果两个图形关于某条直线对称，
成轴对称的两个图形中，
MN 垂直平分BB′.
一个轴对称图形的对称轴是否也具有上述性质呢？
MN 垂直平分AA′,
1、如图，△ABC 与 △DEF 关于直线 MN 对称，则以下结论中错误的是（　 　） A.AB∥DF B.∠B=∠E C.AB=DE D.AD的连线被MN垂直平分
2、如图，Rt△ABC中，∠ACB=90°，∠A=50°，将其折叠，使点A落在边CB上点A′处，折痕为CD，则∠A′DB为_______.
3、如图，正方形 ABCD 的边长为 4cm，则图中阴影部分的面积为(　　 )
A.4cm2 B.8cm2 C.12cm2 D.16cm2
方法归纳：正方形是轴对称图形，在轴对称图形中求不规则的阴影部分的面积时，一般可以利用轴对称变换，将其转换为规则图形后再进行计算.
4、小华在镜中看到身后墙上的钟，你认为实际时间最接近8点的是(　　)
5、想一想：一辆汽车的车牌在水中的倒影如图所示，你能确定该车车牌的号码吗？
问题 1 ：已知对称轴 和一个点A，如何画出点A关于直线 的对称点A′?
点A′就是所要求作的图形.
(1) 过点 A 作直线 的垂线，垂足为点O.
(2) 延长 AO 至A′，使得 OA′=AO；
延长AO至A′,使得 OA′=AO；
问题2：如何画线段AB关于直线 的对称线段A′B′?
(2) 同理，作出点B关于直线 的对称点B′.
(1) 过点A作直线 的垂线，垂足为点O.
(3) 连接点A′，B′，则线段A′B就是′所要求作的图形.
延长AO至A′,使得 OA′=AO；
问题3：如何画线段AB关于直线 的对称线段A′B′?？
(3) 连接A′B′，B′C′，C′A′，得到△ A′B′C′就是所要求作的图形.
(2) 同理，分别作出点B，C关于直线 的对称点B′，C′ .
作已知图形关于某直线对称的图形的一般步骤：
几何图形都可以看作由点组成，对于某些图形，只要作出图形中一些特殊点（如线段端点）的对称点，连接这些对称点，就可以得到原图形的对称图形.
确定图形中的一些特殊点，如线段端点.
画出特殊点关于已知直线的对称点.
1、已知直线 和△ABC（如图），画△A′B′C′ ，使得它与△ABC 关于直线 对称。
2、已知：点 A，B 在直线 l 的异侧，试在直线 l 上确定 一点 P，使 PA+PB 最短.
3、已知：点 A，B 在直线 l 的同侧，试在直线 l 上确定 一点 P，使 PA+PB 最短.
则点 P即为所求
(1) 作出点 A 关于直线 l 的对称点A′.
(2) 连接 A′B.
线段A′B与直线 l 交于点P，
4、古希腊有一个著名的“将军饮马问题”，大致内容如下：古希腊一位将军，每天都要巡查河岸同侧的两个军营A，B．他总是先去A营，再到河边饮马，之后，再巡查B营．他时常想，怎么走，才能使他每天走的路程之和最短呢？
5、如图，已知点 A 是锐角 ∠MON 内的一点，试分别在 OM、ON 上确定点 B、点 C，使 △ABC 的周长最小．写出你作图的主要步骤并标明你所确定的点.(要求画出草图，保留作图痕迹)
解：① 分别作点 A 关于 OM，ON 的对称点 A′，A″； ② 连接A′，A″，分别交 OM，ON 于点 B、点 C，则点 B、 点 C 即为所求．
解决此类问题的方法是分别作出这个点关于两条射线的对称点，然后连接所得的两个对称点，所得线段与两条射线的交点即为所求点.
轴对称解决最短距离的方法：
6、 在3×3的正方形格点图中，有格点△ABC和△DEF，且△ABC和△DEF关于某直线成轴对称，请在下面给出的图中画出4个这样的△DEF.