数学八年级上册2.1 图形的轴对称当堂检测题

这是一份数学八年级上册2.1 图形的轴对称当堂检测题，共12页。试卷主要包含了《西游记》第三十二回写道等内容，欢迎下载使用。
班级： 姓名：
考点一： 轴对称图形识别
例1．中国新能源汽车市场快速增长，成为中国汽车行业的一抹亮色．以下的新能源汽车品牌标志中，不是轴对称图形的是（ ）
A．B．C．D．
变式1-1．数学符号能使数学语言在形式上一目了然，简明准确，它为表述和论证数学理论带来了极大的方便．下列数学符号中，是轴对称图形的为（ ）
A．B．C．D．
变式1-2．如图是沈阳故宫东部区域局部建筑分布图，这种建筑布局体现的设计的理念是（ ）

A．轴对称B．中心对称C．平移D．旋转
考点二：根据轴对称图形特征求解
例2．如图，△ABC与△A′B′C′关于直线l对称，点A、B、C的对应点分别为点A′、B′、C′，若AB=3，则A′B′的长度为（ ）
A．3B．4C．2D．1
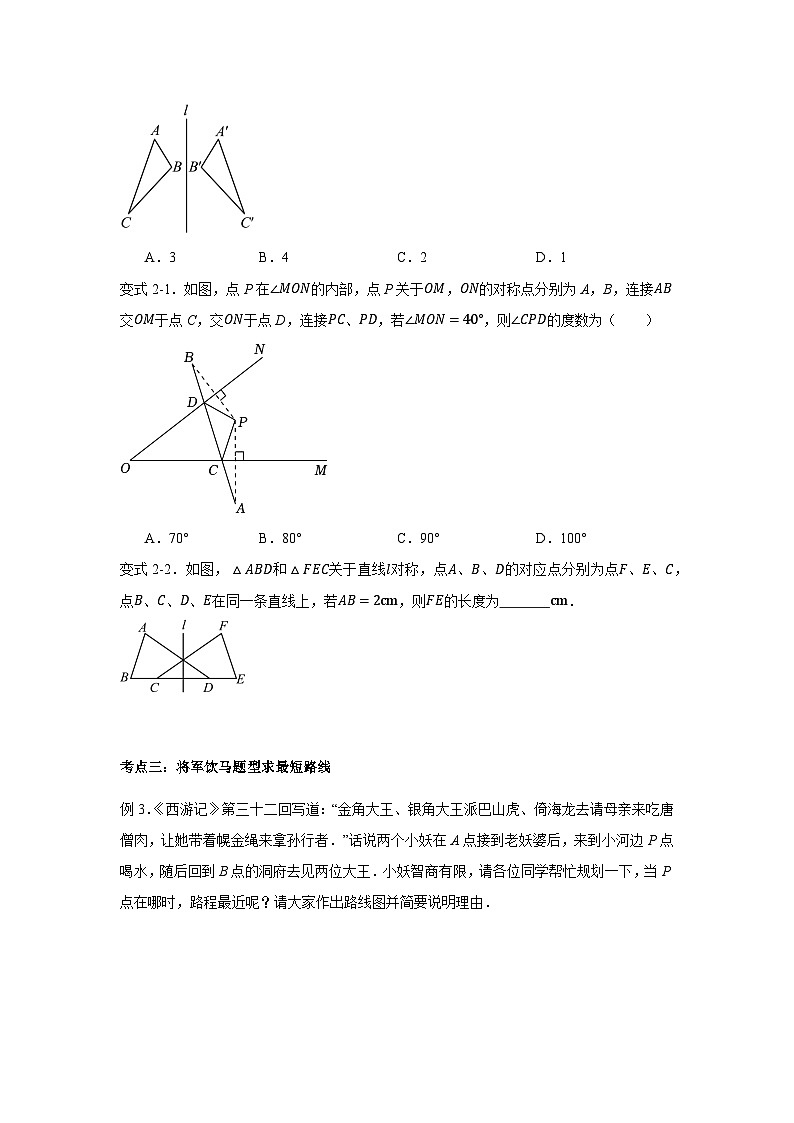
变式2-1．如图，点P在∠MON的内部，点P关于OM，ON的对称点分别为A，B，连接AB交OM于点C，交ON于点D，连接PC、PD，若∠MON=40°，则∠CPD的度数为（ ）
A．70°B．80°C．90°D．100°
变式2-2．如图，△ABD和△FEC关于直线l对称，点A、B、D的对应点分别为点F、E、C，点B、C、D、E在同一条直线上，若AB=2cm，则FE的长度为 cm．
考点三：将军饮马题型求最短路线
例3．《西游记》第三十二回写道：“金角大王、银角大王派巴山虎、倚海龙去请母亲来吃唐僧肉，让她带着幌金绳来拿孙行者．”话说两个小妖在A点接到老妖婆后，来到小河边P点喝水，随后回到B点的洞府去见两位大王．小妖智商有限，请各位同学帮忙规划一下，当P点在哪时，路程最近呢？请大家作出路线图并简要说明理由．

变式3-1．如图，汾河岸边有A，B两个住宅小区，恒富然气公司想在汾河边L上修建一个天然气站，问天然气站位置选在什么地方时，才能使管道铺设用材最少？（写出画法，并保留痕迹）
考点四：轴对称的光反射问题
例4．我们知道光的反射是一种常见的物理现象.如图，某 V 型路口放置如图所示的两个平面镜l1，l2，两个平面镜所成的夹角为∠1，位于点 D 处的甲同学在平面镜l2 中看到位于点A处的乙同学的像，其中光的路径为入射光线AB 经过平面镜l1反射后，又沿BC射向平面镜l2，在点 C 处再次反射，反射光线为CD，已知入射光线AB∥l2，反射光线CD∥l1 ，则∠1等于（ ）
A．40°B．50°C．60°D．70°
变式4-1．如图，在空心圆柱口放置一面平面镜EF，EF与水平线CD的夹角∠EBC=70°，入射光线AB经平面镜反射后反射光线为BM（点A，B，C，D，E，F，M在同一竖直平面内），已知∠ABE=∠FBM．若要使反射光线恰好垂直于圆柱底面射出，则需要把入射光线AB与水平线CD的夹角∠ABC的度数调整为（ ）
A．35°B．40°C．50°D．60°
考点五：折叠问题
例5．如图，将△ABC沿MN折叠，使点C与AB边中点D重合，若AC=6,AB=4，则△ADN的周长为（ ）
A．6B．8C．10D．12
变式5-1．在直角三角形ABC中，∠ACB=90°，D是AB上一点，且∠ACD=∠B．将△ADC沿CD所在直线翻折，点A落在边BD所在直线上，记为点A′．

（1）如图，若∠B=34°，则∠A′CB的度数为 °；
（2）若∠B=n°(n>45)，则∠A′CB的度数为 （用含n的代数式表示）．
变式5-2．如图，△ABC沿EF折叠使点A落在点A′处，BP、CP分别是∠ABD、∠ACD平分线，若∠P=30°，∠A′EB=16°，则∠A′FC= °．

参考答案
考点一： 轴对称图形识别
例1．中国新能源汽车市场快速增长，成为中国汽车行业的一抹亮色．以下的新能源汽车品牌标志中，不是轴对称图形的是（ ）
A．B．C．D．
【详解】
A、∵是轴对称图形，
∴不符合题意；
B、∵是轴对称图形，
∴不符合题意；
C、∵不是轴对称图形，
∴符合题意；
D、∵是轴对称图形，，
∴不符合题意；
故选C．
变式1-1．数学符号能使数学语言在形式上一目了然，简明准确，它为表述和论证数学理论带来了极大的方便．下列数学符号中，是轴对称图形的为（ ）
A．B．C．D．
【详解】解：A、B、C均找不到一条直线，使A、B、C沿该直线折叠后，直线两边的部分能够完全重合，故A、B、C不是轴对称图形，不符合题意；
D能找到一条直线，使D沿该直线折叠后，直线两边的部分能够完全重合，故D是轴对称图形，符合题意；
故选：D．
变式1-2．如图是沈阳故宫东部区域局部建筑分布图，这种建筑布局体现的设计的理念是（ ）

A．轴对称B．中心对称C．平移D．旋转
【详解】解：依题意，∵沈阳故宫东部区域局部建筑分布图符合沿一条直线折叠，直线两旁的部分能够完全重合的特征，
∴这种建筑布局体现的设计的理念是轴对称，
故选：A．
考点二：根据轴对称图形特征求解
例2．如图，△ABC与△A′B′C′关于直线l对称，点A、B、C的对应点分别为点A′、B′、C′，若AB=3，则A′B′的长度为（ ）
A．3B．4C．2D．1
【详解】解：∵△ABC与△A′B′C′关于直线l对称，
∴AB=A′B′=3，
故选：A．
变式2-1．如图，点P在∠MON的内部，点P关于OM，ON的对称点分别为A，B，连接AB交OM于点C，交ON于点D，连接PC、PD，若∠MON=40°，则∠CPD的度数为（ ）
A．70°B．80°C．90°D．100°
【详解】解：根据题意可得：
∠BDN=∠PDN=12∠BDP，∠ACM=∠PCM=12∠ACP，
∵∠MON=40°，∠DOC+∠ODC+∠OCD=180°，
∴∠ODC+∠OCD=180°−40°=140°，
∵∠ODC=∠BDN，∠OCD=∠ACM，
∴∠BDN+∠ACM=140°，
∴∠BDP+∠ACP=280°，
∵∠BDP+∠PDC=180°，∠ACP+∠PCD=180°，
∴∠PDC+∠PCD=360°−280°=80°，
∵∠PDC+∠PCD+∠CPD=180°，
∴∠CPD=100°，
故选：D．
变式2-2．如图，△ABD和△FEC关于直线l对称，点A、B、D的对应点分别为点F、E、C，点B、C、D、E在同一条直线上，若AB=2cm，则FE的长度为 cm．
【详解】解：依题意，FE=AB=2cm，
故答案为：2．
考点三：将军饮马题型求最短路线
例3．《西游记》第三十二回写道：“金角大王、银角大王派巴山虎、倚海龙去请母亲来吃唐僧肉，让她带着幌金绳来拿孙行者．”话说两个小妖在A点接到老妖婆后，来到小河边P点喝水，随后回到B点的洞府去见两位大王．小妖智商有限，请各位同学帮忙规划一下，当P点在哪时，路程最近呢？请大家作出路线图并简要说明理由．

【详解】解：如图，作A点关于小河的对称点A′，连接A′B交小河所在直线于P点；

理由：根据作法得：AP=A′P，
∴PA+PB=PA′+PB=A′B（两点之间，线段最短），
即PA+PB=A′B为最短路径．
变式3-1．如图，汾河岸边有A，B两个住宅小区，恒富然气公司想在汾河边L上修建一个天然气站，问天然气站位置选在什么地方时，才能使管道铺设用材最少？（写出画法，并保留痕迹）
【详解】如图所示：首先作出A点关于汾河边L的对称点A′，再连接A′B，A′B与汾河边L的交点处就是P处，即天然气站位置．
．
考点四：轴对称的光反射问题
例4．我们知道光的反射是一种常见的物理现象.如图，某 V 型路口放置如图所示的两个平面镜l1，l2，两个平面镜所成的夹角为∠1，位于点 D 处的甲同学在平面镜l2 中看到位于点A处的乙同学的像，其中光的路径为入射光线AB 经过平面镜l1反射后，又沿BC射向平面镜l2，在点 C 处再次反射，反射光线为CD，已知入射光线AB∥l2，反射光线CD∥l1 ，则∠1等于（ ）
A．40°B．50°C．60°D．70°
【答案】C
【详解】如图所示，由光的反射定律，可以知道∠5=∠2，∠3=∠4
∵AB∥l2，CD∥l1
∴∠1=∠2，∠1=∠4
∴∠1=∠3=∠5
∵∠1+∠3+∠5=180°
∴∠1=60°
故选：C ．
变式4-1．如图，在空心圆柱口放置一面平面镜EF，EF与水平线CD的夹角∠EBC=70°，入射光线AB经平面镜反射后反射光线为BM（点A，B，C，D，E，F，M在同一竖直平面内），已知∠ABE=∠FBM．若要使反射光线恰好垂直于圆柱底面射出，则需要把入射光线AB与水平线CD的夹角∠ABC的度数调整为（ ）
A．35°B．40°C．50°D．60°
【答案】C
【详解】解：由题意，知∠CBM=90°，
∴∠FBM=180°−70°−90°=20°．
∴∠ABE=20°．
∴∠ABC=∠EBC−∠ABE=70°−20°=50°，
故选：C．
考点五：折叠问题
例5．如图，将△ABC沿MN折叠，使点C与AB边中点D重合，若AC=6,AB=4，则△ADN的周长为（ ）
A．6B．8C．10D．12
【答案】B
【详解】解：△ABC沿MN折叠，使点C与AB边中点D重合，
∴CN=ND，
∵D为AB的中点，
∴DA=12AB=12×4=2，
∴△ADN的周长为：AN+ND+DA=AN+CN+DA=AC+DA=6+2=8，
故选：B．
变式5-1．在直角三角形ABC中，∠ACB=90°，D是AB上一点，且∠ACD=∠B．将△ADC沿CD所在直线翻折，点A落在边BD所在直线上，记为点A′．

（1）如图，若∠B=34°，则∠A′CB的度数为 °；
（2）若∠B=n°(n>45)，则∠A′CB的度数为 （用含n的代数式表示）．
【详解】解：（1）∵∠ACB=90°，
∴∠ACD+∠BCD=90°，
∵∠ACD=∠B，
∴∠B+∠BCD=90°，
∴∠BDC=90°，
∴CD⊥AB．
当∠B=34°时，∠ACD=∠B=34°，∠BCD=90°−∠B=56°，
由折叠知，∠A′CD=∠ACD=34°．
∴∠A′CB=∠BCD−∠A′CD=56°−34°=22°，
故答案为：22；
（2）如图，
，
同（1）的方法得，∠A′CD=n°，∠BCD=90°−n°，
∴∠A′CB=∠A′CD−∠BCD=n°−(90°−n°)=2n−90°，
故答案为：2n−90°．
变式5-2．如图，△ABC沿EF折叠使点A落在点A′处，BP、CP分别是∠ABD、∠ACD平分线，若∠P=30°，∠A′EB=16°，则∠A′FC= °．

【答案】136
【详解】解：如图，设AB、A′F相交于点G，
∵BP、CP分别是∠ABD、∠ACD平分线，
∴∠PBD=12∠ABD，∠PCD=12∠ACD，
∴∠P=∠PBD−∠PCD
=12(∠ABD−∠ACD)
=12∠A，
∴∠A=2∠P=60°，
由折叠得∠A′=∠A=60°，
∴∠AGF=∠A′EB+∠A′=16°+60°=76°，
∴∠A′FC=∠AGF+∠A=76°+60°=136°；
故答案为：136．