



青岛版(2024)九年级上册3.3 圆周角优秀第1课时测试题
展开题型一 圆周角概念的理解
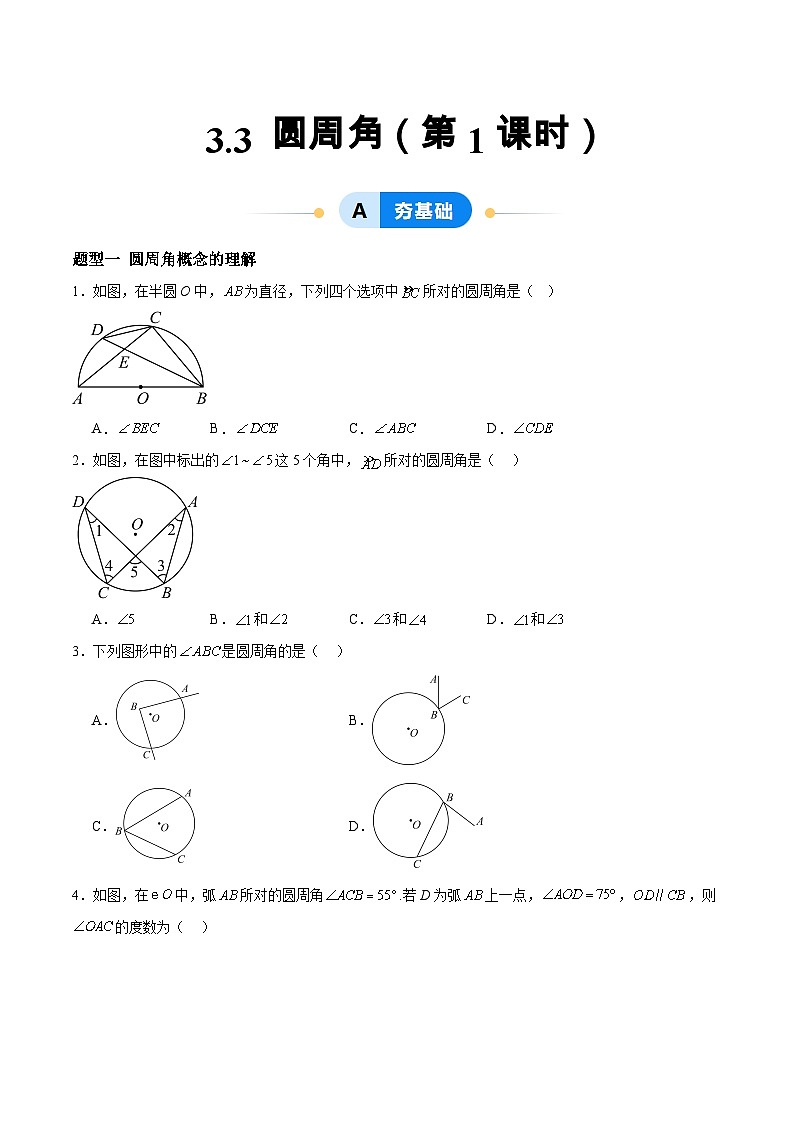
1.如图,在半圆O中,为直径,下列四个选项中所对的圆周角是( )
A. B. C. D.
【答案】D
【分析】本题考查的是圆周角的定义,根据圆周角的定义解答即可,熟知顶点在圆上,并且两边都与圆相交的角叫做圆周角是解题的关键.
【详解】解:所对的圆周角是与,
故选:D.
2.如图,在图中标出的这5个角中,所对的圆周角是( )
A.B.和C.和D.和
【答案】C
【分析】根据圆周角的定义逐个选项判断即可解答.本题考查了圆周角的定义,熟记定义“顶点在圆上,两边和圆相交的角叫圆周角”是解题的关键.
【详解】解:是所对的圆周角,
是所对的圆周角,
是所对的圆周角,
是所对的圆周角,
不是圆周角,
故选:C.
3.下列图形中的是圆周角的是( )
A.B.
C.D.
【答案】C
【分析】由圆周角的定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角,即可求得答案.
【详解】解:由圆周角的定义可知,A、B、D中的都不是圆周角,C中的是圆周角,
故选C.
【点睛】此题考查了圆周角定义.此题比较简单,解题的关键是理解圆周角的定义.
4.如图,在中,弧所对的圆周角.若D为弧上一点,,,则的度数为( )
A.B.C.D.22°
【答案】B
【分析】本题考查了平行线的性质,三角形的外角的性质,延长交于点,根据平行线的性质得出,根据邻补角得出,根据三角形的外角的性质,即可求解.
【详解】解:如图所示,延长交于点,
∵,
∴,
∵,
∵,
∴,
故选:B.
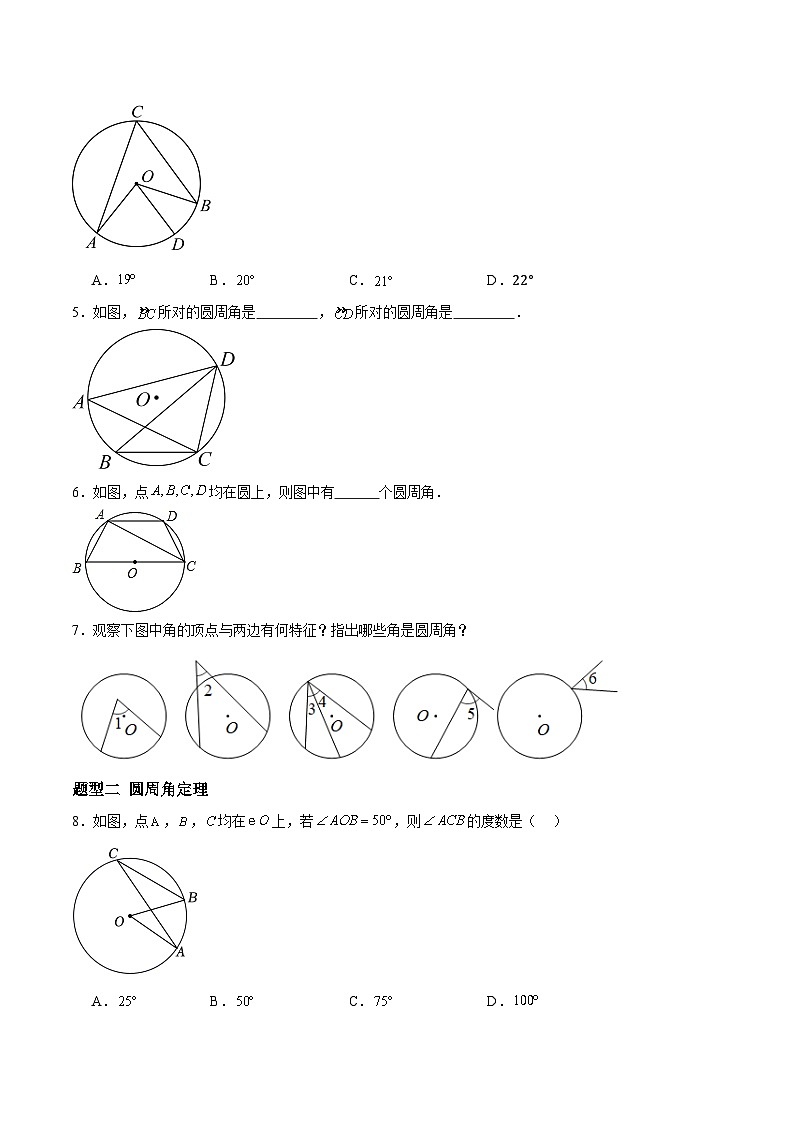
5.如图,所对的圆周角是 ,所对的圆周角是 .
【答案】
【分析】根据圆周角的定义即可解答.
【详解】解:如图,
所对的圆周角是,
所对的圆周角是.
故答案为:;.
【点睛】本题考查了圆周角,顶点在圆周上,并且两边都和圆相交的角叫做圆周角.
6.如图,点均在圆上,则图中有 个圆周角.
【答案】8
【分析】根据圆周角的定义,圆周角的顶点必在圆周上,据此可把顶点分别为A、B、C、D的圆周角数出来,即可得到答案.
【详解】解:以点为顶点的圆周角各有3个,以点为顶点的圆周角各有1个,共有8个圆周角.
故答案为8.
【点睛】本题考查圆周角的定义和分类思想的应用,根据圆周角的定义对图中圆周角进行分类统计即可得到正确答案.
7.观察下图中角的顶点与两边有何特征?指出哪些角是圆周角?
【答案】特征见解析,(c)图中∠3、∠4、∠BAD是圆周角
【详解】解: (a)∠1顶点在⊙O内,两边与圆相交,所以∠1不是圆周角;
(b)∠2顶点在圆外,两边与圆相交,所以∠2不是圆周角;
(c)图中∠3、∠4、∠BAD的顶点在圆周上,两边均与圆相交,所以∠3、∠4、∠BAD是圆周角.
(d)∠5顶点在圆上,一边与圆相交,另一边与圆不相交,所以∠5不是圆周角;
(e)∠6顶点在圆上,两边与圆均不相交,由圆周角的定义知∠6不是圆周角.
【点睛】本题主要考查了圆周角的定义,熟练掌握顶点在圆上,并且两边都和圆相交的角叫做圆周角是解题的关键.
题型二 圆周角定理
8.如图,点,,均在上,若,则的度数是( )
A.B.C.D.
【答案】A
【分析】本题考查了圆周角定理,熟练掌握圆周角定理是解题的关键,直接根据圆周角定理即可得解。
【详解】解:∵,
∴,
故选:.
9.如图,内接于,,则的度数是( )
A.B.C.D.
【答案】B
【分析】本题考查了圆周角定理,在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
直接根据圆周角定理求解即可.
【详解】由题意得:.
故选:B.
10.如图,是的外接圆,若,则的度数是( )
A.B.C.D.
【答案】B
【分析】本题考查圆周角定理.首先根据等腰三角形的性质及三角形内角和定理求出的度数,再利用圆周角与圆心角的关系求出的度数.
【详解】解:中,,,
∴,
∴.
故选:B.
11.如图,是的弦,半径于点D,,点P在圆周上,则等于( )
A.B.C.D.
【答案】C
【分析】本题考查了圆周角定理,垂径定理,熟练掌握定理是解题的关键.由垂径定理得到,根据圆周角定理得到,由半径于点推出是直角三角形,即可求得.
【详解】解:半径于点,
,
,
是直角三角形,
.
故选:C.
12.如图,的直径弦,连接,,若,则的度数为( )
A.B.C.D.
【答案】A
【分析】先根据垂直的条件可计算出,再根据圆周角定理得到,然后利用得到即可.
本题考查圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了等边对等角,直角三角形两锐角互余.掌握圆周角定理是解题的关键.
【详解】解:,
,
,
,
.
故选:A.
13.如图,是的直径,位于两侧的点C,D均在上,,则 度.
【答案】75
【分析】本题考查圆周角定理,补角求出,根据同弧所对的圆周角是圆心角的一半,进行求解即可.
【详解】解:∵是的直径,位于两侧的点C,D均在上,,
∴,
∴;
故答案为:75.
14.如图,A,B,C是上三点,,则的度数是 °.
【答案】45
【分析】
本题考查的是圆周角定理的应用,直接利用圆周角定理可得.
【详解】解:∵,,
∴,
故答案为:
15.如图,在中,,,则的度数为
【答案】/45度
【分析】此题考查了圆周角定理,熟记圆周角定理是解题的关键.根据在同圆或等圆中,相等的弧所对的圆心角相等即可得到结论.
【详解】解:∵,
,
,
∴,
故答案为:.
16.如图,已知点A,B,C在上,C为弧的中点.若,则等于 .
【答案】/140度
【分析】本题考查圆周角定理,弧、弦、圆心角的关系,连接,根据等弧所对的圆心角相等,可得,根据同弧所对的圆周角等于圆心角的一半,可得,由此可解,熟练掌握知识点的应用是解题的关键.
【详解】解:连接,
∵为的中点,
∴,
∴,
∵,,
∴,
∴,
∴,
故答案为:.
17.如图,点A、B、C都在圆O上,OC⊥OB,点A在劣弧上,且OA=AB,求∠ABC的度数.
【答案】∠ABC=15°,
【分析】易知△OAB是等边三角形,可知∠AOB=60°,结合OC⊥OB可得∠COA的度数,由圆周角定理即知∠ABC的度数.
【详解】解:∵OA=OB,OA=AB,
∴OA=OB=AB,
即△OAB是等边三角形,
∴∠AOB=60°.
∵OC⊥OB,
∴∠COB=90°,
∴∠COA=90°﹣60°=30°,
∴∠ABC==15°.
【点睛】本题主要考查了等边三角形的判定和性质及圆周角定理,灵活的利用等边三角形的性质及同弧所对的圆周角是圆心角的一半是解题的关键.
18.如图,是的弦,,求弦所对的圆周角的度数.
【答案】或
【分析】本题考查圆周角定理,首先根据,可得,然后根据三角形的内角和定理,判断出,最后根据圆周角定理,判断出弦所对的圆周角是多少即可.
【详解】解:∵,
∴,
∴,
∴弦所对的圆周角的度数是:;
∵弦所对的优弧的度数为:,
∴弦所对的圆周角的度数是:;
综上,可得弦所对的圆周角的度数是或.
19.已知弦把圆周分成两部分,则弦所对圆周角的度数为( )
A.B.C.或D.或
【答案】D
【分析】分优弧,劣弧两种情况,求解即可.
【详解】解:∵弦把圆周分成两部分,
∴劣弧的度数为:,即:劣弧所对的圆周角的度数为,
优弧的度数为:,即:优弧所对的圆周角的度数为,
∴弦所对圆周角的度数为或;
故选:D.
【点睛】本题考查弦,弧,角之间的关系,解题的关键是注意弦分弧为优弧和劣弧两种情况.
20.如图,在图中标出的4个角中,圆周角有( )
A.1个B.2个C.3个D.4个
【答案】B
【分析】本题考查了圆周角的定义,顶点在圆周上,并且角的两边与圆相交的角叫做圆周角,由此即可得出答案,熟练掌握圆周角的定义是解此题的关键.
【详解】解:由图可得:和符合圆周角的定义,顶点不在圆周上,的一边和圆不想交,
故图中的圆周角有和,共个,
故选:B.
21.如图,、是的弦,且,若,则的度数为( )
A.B.C.D.
【答案】D
【详解】此题考查了圆心角、弧的关系,熟练掌握圆心角、弧的关系是解题的关键.
根据圆心角、弧、弦的关系求出,再根据等腰三角形的性质求解即可.
【解答】解:如图,连接,
,
,
,
,
,
,
.
故选:D.
22.如图,为圆O的直径,弦与交于点E,为等腰三角形,为底,,求圆弧所对的圆心角( )
A.B.C.D.
【答案】A
【分析】本题主要考查了圆周角定理,等腰三角形的性质.连接,,根据圆周角定理可得,再由,可得,从而得到,再由圆周角定理可得,即可求解.
【详解】解:如图,连接,,
∵为等腰三角形,为底,,
∴,,
∵,
∴,
∴,
∴,
∴圆弧所对的圆心角为.
故选:A
23.如图,是的直径,弦垂直平分,点在上,连接,,则 .
【答案】60°/60度
【分析】本题考查了垂直平分线的性质,等边三角形的性质,圆周角定理.连接,根据垂直平分线的性质可得,由等边三角形的性质可得,再根据圆周角定理即可得到答案.
【详解】解:如图,连接,
是的直径,弦垂直平分,
,
是等边三角形,则,
,
,
故答案为:.
青岛版(2024)九年级上册3.4 直线与圆的位置关系精品第1课时同步达标检测题: 这是一份青岛版(2024)九年级上册<a href="/sx/tb_c75361_t7/?tag_id=28" target="_blank">3.4 直线与圆的位置关系精品第1课时同步达标检测题</a>,文件包含34直线与圆的位置关系第1课时分层作业解析版docx、34直线与圆的位置关系第1课时分层作业原卷版docx等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。
初中数学青岛版(2024)九年级上册第3章 对圆的进一步认识3.3 圆周角精品第2课时课时练习: 这是一份初中数学青岛版(2024)九年级上册<a href="/sx/tb_c75360_t7/?tag_id=28" target="_blank">第3章 对圆的进一步认识3.3 圆周角精品第2课时课时练习</a>,文件包含33圆周角第2课时分层作业原卷版docx、33圆周角第2课时分层作业解析版docx等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。
初中数学青岛版(2024)九年级上册3.2 确定圆的条件优秀第2课时测试题: 这是一份初中数学青岛版(2024)九年级上册<a href="/sx/tb_c75359_t7/?tag_id=28" target="_blank">3.2 确定圆的条件优秀第2课时测试题</a>,文件包含32确定圆的条件第2课时分层作业原卷版docx、32确定圆的条件第2课时分层作业解析版docx等2份试卷配套教学资源,其中试卷共10页, 欢迎下载使用。














