


初中青岛版(2024)1.4 图形的位似优质ppt课件
展开1 . 4 图形的位似
1. 会用图形的坐标的变化来表示图形的位似变换,掌握把一个图形按一定大小比例放大或缩小后,点的坐标变化的规律. 2.了解四种变换(平移、轴对称、旋转和位似)的异同,并能在复杂图形中找出这些变换.
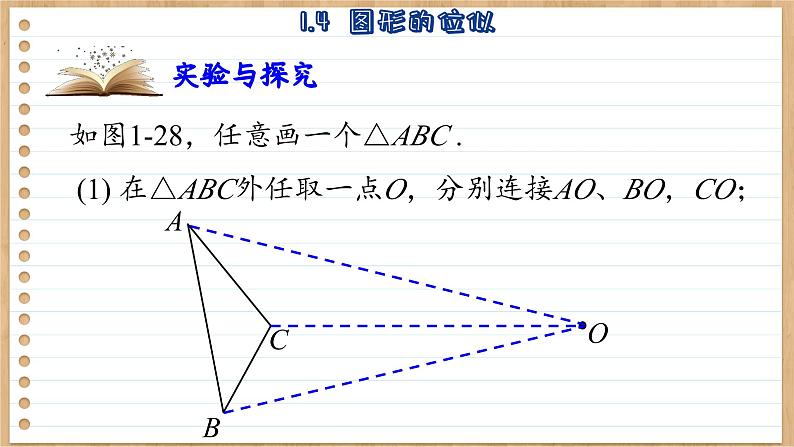
如图1-28,任意画一个△ABC . (1) 在△ABC外任取一点O,分别连接AO、BO,CO;
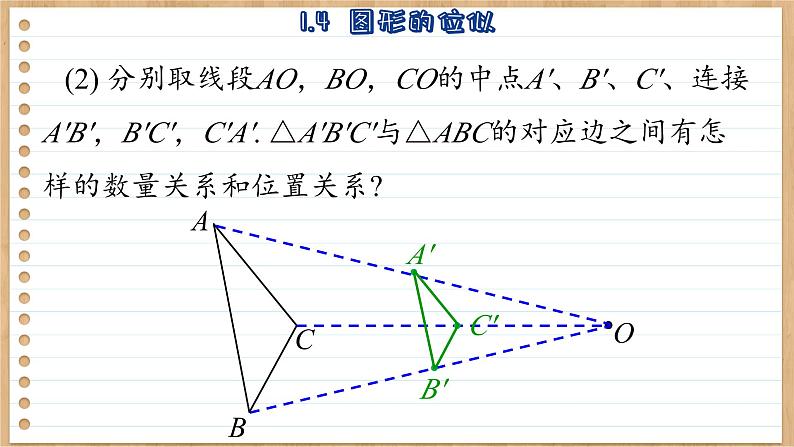
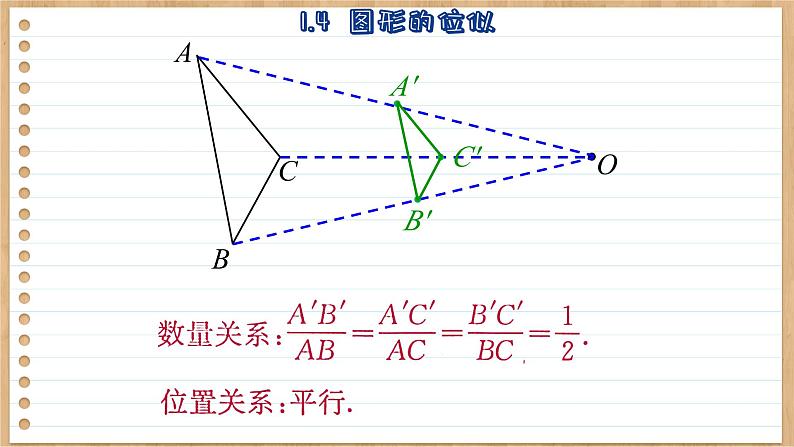
(2) 分别取线段AO,BO,CO的中点A′、B′、C′、连接 A′B′,B′C′,C′A′. △A′B′C′与△ABC的对应边之间有怎样的数量关系和位置关系?
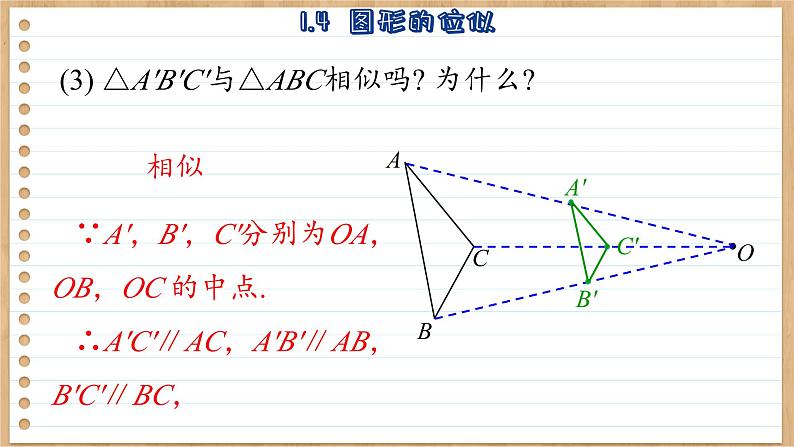
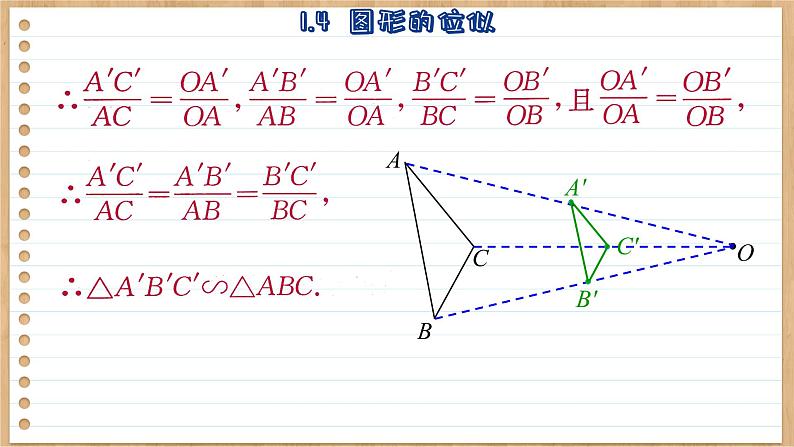
(3) △A′B′C′与△ABC相似吗? 为什么?
∵A′,B′,C′分别为OA,OB,OC 的中点. ∴A′C′∥AC,A′B′∥AB,B′C′∥BC,
(4) 在图中,如果点A′′是 OA上的任意一点,过A′′作A′′B′′//AB交OB于点B′′,作A′′C′′//AC交OC于点C′′,连接B′′C′′,△A′′B′′C′′与△ABC相似吗?为什么?
(5) △ABC与△A′B′C′,△A′′B′′C′′的每对对应点所在的 直线有怎样的位置关系?
每对对应点所在的直线都经过同一点.
像这样,对应边互相平行(或共线)且每对对应点所在的直线都经过同点的两个相似多边形叫做位似图形 ,这个点叫做位似中心.
在图中,△ABC与△A′B′C′,△A′′B′′C′′都是位似图形,点O是位似中心.
(6) 在图 中,利用位似,由△ABC得到与它相似的△A′B′C′,你发现△ABC的边长缩小了几分之一? 反过来,由△A′B′C′也可以利用位似得到与它相似的△ABC,这时△A′B′C′的边长扩大了多少倍?
一般地,位似可以看作是图形的一种位置和大小的变化,位似不改变图形的形状,利用位似可以将一个图形放大或缩小.
(7) 如图①②③,四边形ABCD与四边形A′B′C′D′都是位似图形,你发现它们的位似中心的位置有什么不同?
在图①中,位似中心O在两个图形的外部; 在图②中,位似中心O在两个图形的内部; 在图③中,位似中心A在两个图形的公共顶点A(A′)处. 你还能画出四边形 ABCD与A′B′C′D′ 位似时,位似中心的其他可能位置吗?与同学交流.
如图,已知△ABC与点O. 以点O为位似中心,画出△A′B′C′,使它与△ABC是位似图形,并且相似比为 3∶2.
(1) 作射线OA,OB,OC ;
(3) 连接A′B′,B′C′,C′A′.
(1) 作射线 AO,BO,CO ;
2. 下图中的两个三角形是位似图形吗? 如果是,画出它的位似中心.
是位似图形.如图所示,任意两对对应点的连线的交点O就是位似中心.
3. 如图,AB与CD相交于点E,AC//DB. △ACE与△BDE是位似图形吗? 为什么?
解:是位似图形· ∵AC//DB, ∴∠A =∠B,∠C=∠D, ∴△ACE ∽ △BDE. ∵点A与点B,点C与点D, 点E与点E 所在的直线都经过点E, ∴ △ACE 与△BDE 是位似图形
(1) 如图,在直角坐标系中,矩形 OABC的顶点坐标分别 为(0,0),(6,0),(6,4),(0,4). 如果将点O,A,B, C的横、纵坐标都缩小一半得到 点O′,A′,B′,C′,顺次连接点 O′,A′,B′,C′,得到了一个怎 样的图形?
(2) 四边形O′A′B′C′与矩形OABC是位似图形吗?如果是, 位似中心是哪个点?它们的相似比是多少?
如图,点O′与点O重合,点A′,B′,C′的坐标分别为(3,0),(3,2),(0,2).
顺次连接点O,A′,B′,C′,因为∠xOy是直角,由A′,B′的横坐标相等,可知 B′A′⊥x轴,从而∠OA′B′是直角. 类似地,∠OC′B′也是直角,从而四边形 OA′B′C′是矩形.
由于点B′的坐标(3,2) 适合上式,故点B′在直线OB上. 又由点A与A′在x轴上,点C与C′在y轴上, 因此矩形OA′B′C′与矩形 OABC的对应顶点所在的直线都经过同点O,
且对应边A′B′//AB,B′C′//BC,OA′与OA,OC′与OC分别在x轴、y轴上,所以矩形 OA′B′C′与矩形OABC是位似图形,点O是它们的位似中心.
(3) 如图,已知△OAB 的顶点O是标原点,顶点A,B的坐标分别为(-1,2),(-3,0).把△OAB 各个顶点的横、纵坐标都扩大到原来的 3 倍,得到点O′,A′,B′. 连接O′A′,O′B′,A′B′,△O′A′B′与△OAB是位似图形吗? 如果是,位似中心是哪个点?
△O′A′B′与△OAB是位似图形,位似中心是坐标原点.
(4) 由(1)(2)(3) 你能得出什么结论?
如果多边形有一个顶点在坐标原点,有一条边在x轴上,那么将这个多边形的顶点坐标分别扩大(或缩小)相同的倍数,所得到的图形与原图形是位似图形,坐标原点是它们的位似中心.
上面得到的结论还能推广吗?如果能,说出你推广后的结论,与同学交流.
如图,四边形OABC的顶点坐标分别为(0,0),(2,0),(4,4),(-2,2).
(2) 画出四边形OA′B′C′.
1. 如图,□OABC的一个顶点 是坐标原点,点A的坐标是 (4,0),点 C的坐标是 ( 2,-2 ).
(1) 求点B的坐标;
点B的坐标是(6, - 2).
(2) 画出以点O为位似中心,与□OABC位似的图形, 使它与□ OABC的相似比为1∶2.
取点A′(2,0),B′(3, -1),C′(1, -1),描点并顺次连接,作出四边形 OA′B′C′.
另取点A′′(-2,0),B′′(-3,1),C′′(-1,1),描点并顺次连接,作出四边形OA′′B′′C′′,
则四边形 OA′B′C′,OA′′B′′C′′ 都是所求的图形.
1. 判断满足下列条件的两个三角形是不是位似图形, 如果是,指出位似中心.
(1) 如图①所示,AB,CD相交于点O,且∠B=∠D, AD=CB;
(2) 如图②所示,AB,CD相交于点O,且∠B=∠A.
是位似图形,位似中心是点 O.
2. 如图,在△ABC中,E,F是AB 的三等分点,FH//EG//AC. (1) 四边形EFHG与四边形FACH是位似图形吗?为什么?
(2) 指出图中所有的位似图形.
△BEG 与△BFH 是位似图形,△BEG 与△BAC是位似图形,△BFH 与△BAC 是位似图形.
4. 如图,△ABC为正三角形,点A与B的坐标分别为(- 1,0),(1,0). 以点C为位似中心,在点C下方画出一个与△ABC位似的图形,使它与△ABC的相似比为 2∶1.
5. 如图,点O是等边三角形ABC的中心,P,Q,R分别是OA,OB、OC 的中点说明△ABC与△PQR是位似图形,并求出它们的相似比.
6. 如图,在6×8的网格图中,每个小正方形的边长均为1. 点O和△ABC的顶点均是格点. 以O为位似中心,在网格中画出与△ABC位似,且相似比为 1∶2 的顶点均是格点的三角形.
7. 如图,小亮要从三角形木板ABC上锯下一块正方形木板,使正方形的一边在ABC的边AB上,另外两个顶点分别在边AC,BC上.他采用了以下的方法:
(1) 在AC边上取一点G,作GD⊥AB,垂足为D,以GD为 一边在△ABC内作正方形GDEF;(2) 连接AF并延长交AC于点F;(3) 过点F作AB的平行线交AC 于点G,分别过 G′,F′作 AB的垂线,垂足分别为点D′, E′.所得到的四边形D′E′F′G′就是满足条件的正方形.
小亮的作法正确吗?为什么?
解:小亮的作法是正确的. ∵G′D′⊥AB,F′E′⊥ AB,G′F′//AB, ∴G′D′⊥G′F′,F′E′⊥G′F′. ∴四边形DEFG是矩形. 在正方形 GDEF 中, GF//AB
青岛版九年级上册1.4 图形的位似获奖ppt课件: 这是一份青岛版九年级上册<a href="/sx/tb_c99056_t3/?tag_id=26" target="_blank">1.4 图形的位似获奖ppt课件</a>,共27页。PPT课件主要包含了课堂导入,探究新知,课堂练习等内容,欢迎下载使用。
初中数学青岛版九年级上册1.4 图形的位似评优课ppt课件: 这是一份初中数学青岛版九年级上册<a href="/sx/tb_c99056_t3/?tag_id=26" target="_blank">1.4 图形的位似评优课ppt课件</a>,共31页。PPT课件主要包含了课堂导入,探究新知,位似的特征,概念理解,位似图形的画法,课堂练习等内容,欢迎下载使用。
初中青岛版1.4 图形的位似教学演示ppt课件: 这是一份初中青岛版1.4 图形的位似教学演示ppt课件,共19页。PPT课件主要包含了学习目标,复习导入,新知探究,例题讲解,随堂练习,-2-4,-2-4-6等内容,欢迎下载使用。













