初中数学华东师大版（2024）七年级上册2.4 绝对值完整版课件ppt

这是一份初中数学华东师大版（2024）七年级上册2.4 绝对值完整版课件ppt，共18页。PPT课件主要包含了教学目标，新知导入，绝对值，新知讲解，利用绝对值的概念口答，针对训练，例2化简，课堂练习，填一填，或-2等内容，欢迎下载使用。

【教学目标】1．让学生能根据一个数的绝对值表示“距离”，初步理解绝对值的概念；2．让学生学会求一个数的绝对值，渗透数形结合的思想；3．学会绝对值的计算，并能应用绝对值解决实际问题，体会绝对值的意义和作用．【重点】绝对值的概念和求一个数的绝对值．【难点】绝对值的几何意义和代数意义．
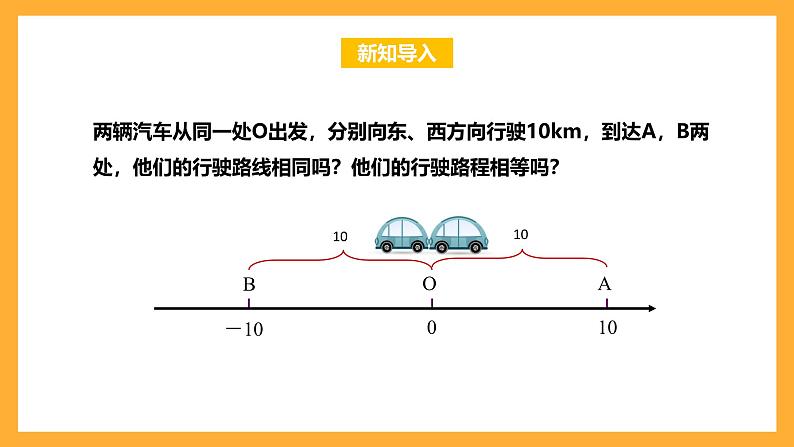
两辆汽车从同一处O出发，分别向东、西方向行驶10km，到达A，B两处，他们的行驶路线相同吗？他们的行驶路程相等吗？
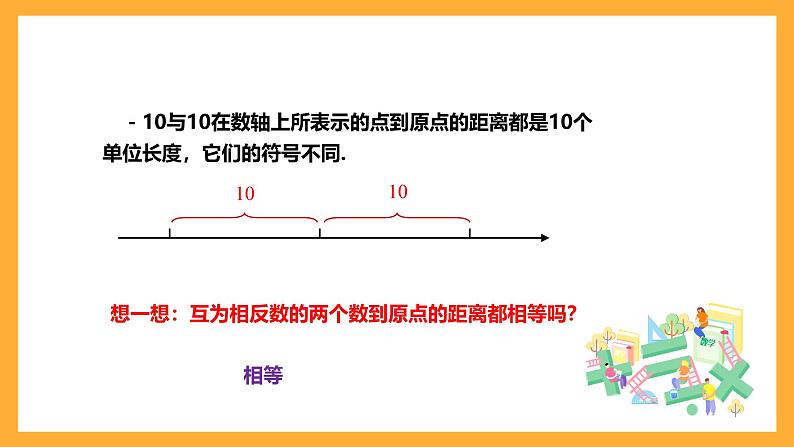
　－10与10在数轴上所表示的点到原点的距离都是10个单位长度，它们的符号不同.
　想一想：互为相反数的两个数到原点的距离都相等吗？
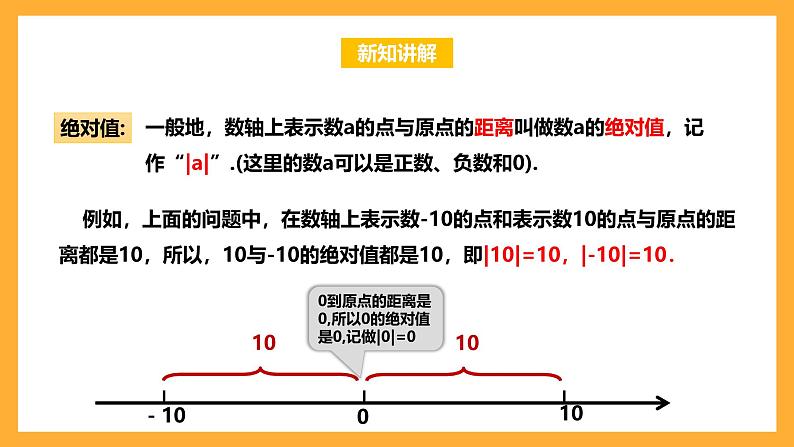
一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值，记作“|a|”.(这里的数a可以是正数、负数和0).
例如，上面的问题中，在数轴上表示数-10的点和表示数10的点与原点的距离都是10，所以，10与-10的绝对值都是10，即|10|=10，|-10|=10．
0到原点的距离是0,所以0的绝对值是0,记做|0|=0
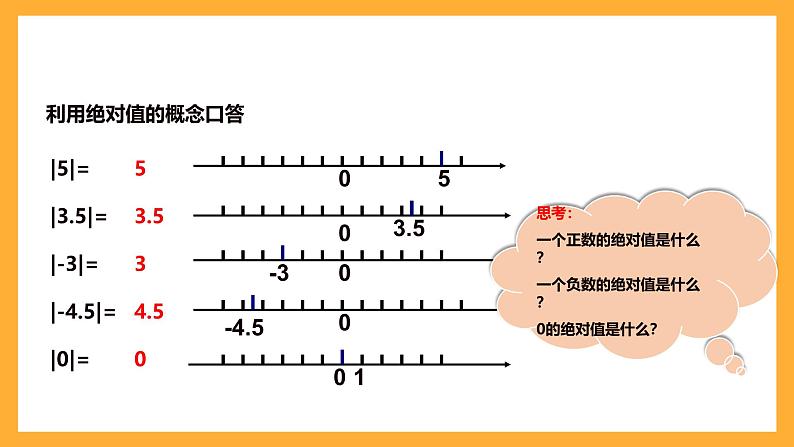
|5|=|3.5|= |-3|=|-4.5|=|0|=
思考： 一个正数的绝对值是什么？一个负数的绝对值是什么？0的绝对值是什么？
由绝对值的意义，我们可以知道：1.一个正数的绝对值是它本身；2.零的绝对值是零；3.—个负数的绝对值是它的相反数.
绝对值的性质表述成： (1)如果a＞0，那么|a|＝a； 　　 (2)如果a＜0，那么|a|＝-a； (3)如果a＝0，那么|a|＝0. 　　　　　　
由此可以看出，任何一个有理数的绝对值总是正数或0（通常也称非负数）.即对任意有理数a，总有
（1）一个数的绝对值是4 ，则这个数是－4. 　　　　　　　 　　　　　　　　　 （2）有理数的绝对值一定是正数.　（3）若a＝－b，则|a|＝|b|.　　　　　　　　（4）若|a|＝|b|，则a＝b.（5）若|a|＝－a，则a必为负数.　　　　 　（6）互为相反数的两个数的绝对值相等.
1.判断下列说法是否正确.
①绝对值等于一个正数的数有两个，它们互为相反数.
②有理数的绝对值一定是非负数.
③互为相反数的两个数的绝对值相等.
⑤绝对值等于它的相反数的数是非正数.
④如果两个数的绝对值相等，则这两个数相等或互为相反数.
例1 求下列各数的绝对值：
3. |a|＋|b|=|a＋b|，则a，b关系是(　　) A. a，b的绝对值相等 B. a，b异号 C. a＋b的和是非负数 D. a，b同号或其中至少一个为零
4.若|a-1|=a-1，则a的取值范围是(　　) A．a≥1 B．a≤1 C．a＜1 D．a＞1
(1)绝对值等于0的数是___；(2)绝对值等于5.25的正数是________；(3)绝对值等于5.25的负数是______；(4)|－ |的相反数是 ；若|a|=2，则a=___________.
6.如图，数轴上的点A所表示的是有理数a，则点A到原点的距离是 .
解析：由数组可以看出，点A到原点的距离为a，因为a小于0，由绝对值的意义可知，点A到原点的距离为-a.
解：根据题意可知x－4＝0，y－3＝0，所以x＝4，y＝3，故x＋y＝7。
【解析】一个数的绝对值总是大于或等于0，即为非负数，若两个非负数的和为0，则这两个数同时为0。
【点睛】几个非负数的和为0，则这几个数都为0。
2.绝对值性质：一个正数的绝对值是它本身，一个负数的绝对值是它的相反数，0的绝对值是0.
3.绝对值的非负性：|a|≥0