初中数学华东师大版（2024）七年级上册第3章 整式的加减3.4 整式的加减2 合并同类项优质课件ppt

这是一份初中数学华东师大版（2024）七年级上册第3章 整式的加减3.4 整式的加减2 合并同类项优质课件ppt，共25页。PPT课件主要包含了教学目标，新课导入，同类项的系数相加，新知探究，＝4x2－3x2，－8x＋6x，5－4，－2x，加法交换律和结合律，针对训练等内容，欢迎下载使用。

【教学目标】1、掌握合并同类项的方法;2、解答题时步骤要规范;3、培养学生分析问题的能力，并培养其创造性。【重点】合并同类项的方法。【难点】合并同类项的步骤的规范化。
每本练习本m元，甲买了5本，乙买了2本，两人一共花了多少元？甲比乙多花了多少元？
解：理解1：甲买了5本，花费5m元，乙买了2本，花费2m元，所以共花了（5m+2m）元，甲比乙多花了（5m-2m)元.
理解2：甲买了5本，乙买了2本，一共买了7本，所以共花7m元.甲比乙多买3本，甲比乙多花3m元.
由上边的例子你发现了什么？
5m+2m=7m 5m-2m=3m
观察这两个式子，你有什么启发？
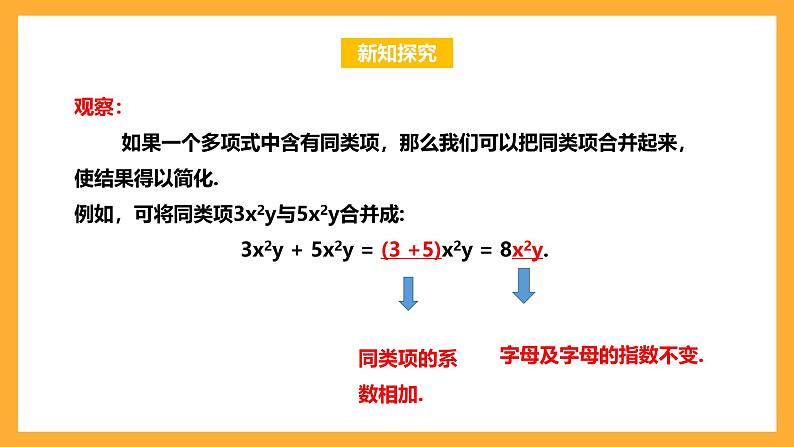
观察： 如果一个多项式中含有同类项，那么我们可以把同类项合并起来，使结果得以简化.例如，可将同类项3x2y与5x2y合并成:3x2y + 5x2y = (3 +5)x2y = 8x2y.
字母及字母的指数不变.
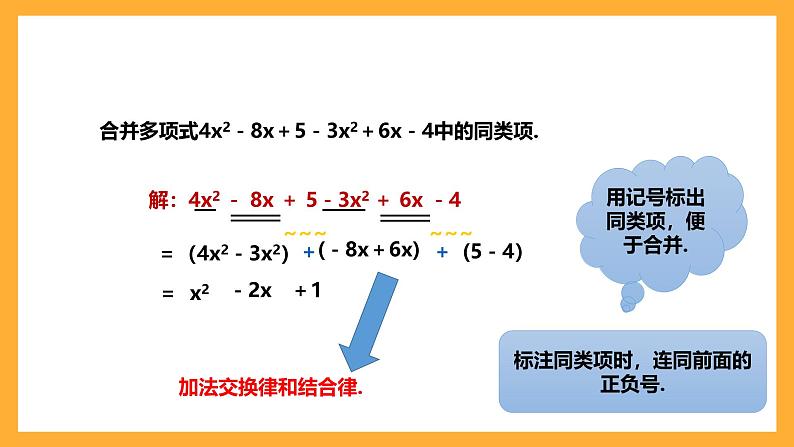
解：4x2 － 8x ＋ 5－3x2 ＋ 6x －4
~~~ ~~~
＝ x2
合并多项式4x2－8x＋5－3x2＋6x－4中的同类项.
— ——
+ +
用记号标出同类项，便于合并.
标注同类项时，连同前面的正负号.
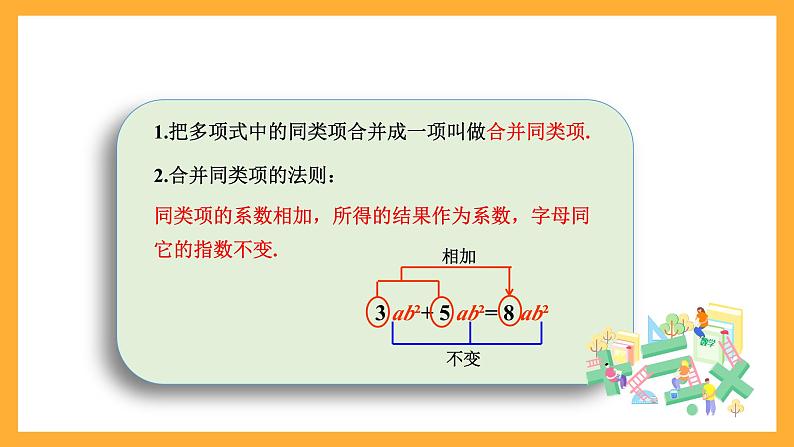
2.合并同类项的法则：
同类项的系数相加，所得的结果作为系数，字母同它的指数不变.
1.把多项式中的同类项合并成一项叫做合并同类项.
3 ab²+ 5 ab²= 8 ab²
下列合并同类项合并对了吗？不对的，说明理由.
（1）a+a=2a（2）3a+2b=5ab（3）5y2-3y2=2
（4）4x2y-5xy2=-x2y（5）3x2+2x3=5x5（6）a+a-5a=-3a
注：（2）（4）（5）中的单项式不是同类项，不能合并. （3）是同类项，但合并结果不对.
例3 合并下列多项式中的同类项:(1) 2a2b - 3a2b + a2b;(2) a3-a2b + ab2 +a2b - ab2 +b3.
解：(1) 2a2b - 3a2b + a2b
(2) a3-a2b + ab2 +a2b - ab2 +b3=a3+（-a2b+a2b）+（ab2-ab2）+b3=a3+（-1+1）a2b+（1-1）ab2+b3=a3+b3
用记号标出各同类项， 便于合并。
“合并同类项”的方法：一找，找出多项式中的同类项，不同类的同类项用不同的标记标出；二移，利用加法的交换律、结合律，将不同类的同类项集中到不同的括号内；三并，将同一括号内的同类项相加即可.
下列各题计算的结果对不对？如果不对，指出错在哪里？
错因：不是同类项不能合并
错因：系数合并对了，但是字母和字母的指数不变
合并同类项时要注意“一相加，两不变”：“一相加”是指各同类项的系数相加；“两不变”是指字母连同它的指数不变.
例4 求多项式3x2 +4x -2x2-x +x2-3x-1的值,其中x =-3.解：3x2 +4x-2x2-x+x2-3x-1=(3 -2 + 1)x2+(4-1-3)x-1= 2x2-1当x =-3时,原式=2x(-3)2-1= 17.
先合并同类项，再求值，比较简便。
解：3x2 +4x-2x2-x+x2-3x-1=3×(-3)2 +4×(-3)-2×(-3)2-(-3)+(-3)2-3×(-3)-1= 17
如果x=0,如何求值比较简便?
如果x=0,直接代人求值比较简便
总结：在求多项式的值时，可以先将多项式中的同类项合并， 然后再求值，这样做往往可以简化计算.
把x=-3直接代人例4中的多项式，求出它的值.与上面的解法比较一下,哪个解法更简便?
例5 如图所示的窗框，上半部分为半圆，下半部分为6个大小一样的长方形,长方形的长和宽的比为3:2.(1)设长方形的长为x米,用x表示所需材料的长度(重合部分忽略不计);(2)分别求出当长方形的长为0.4米、0.5米、0.6米时,所需材料的长度(精确到0.1米,取π≈3.14).
解(1)设长方形的长为x米,则它的宽为气 x米由图不难知道,做这个窗框所需材料的长度为11x+9. x +πx= (11 +6+π)x= (17 + π)x(米).
(2)当x = 0.4时，(17 + π)x≈(17 +3.14) x0.4= 8.056≈8.1.所以,当长方形的长为0. 4米时，所需材料的长度约为8.1米.
1.合并同类项3x2y-2x2y=(3-2)x2y=x2y时,依据的运算律是(　　)A.加法交换律 B.乘法交换律C.分配律的逆用 D.乘法结合律2.将多项式4ab+5a2-5ab-4a2中的同类项分别结合在一起应为(　　)A.(5a2-4a2)+(4ab-5ab) B.(5ab-4a2)-(5a2+4ab)C.(4ab-4a2)+(5a2-5ab) D.(4ab-5a2)-(5ab-4a2)
3．合并下列各式的同类项：(1)5m＋2n－m－3n；(2)3a2－1－2a－5＋3a－a2；(3)－5m2n＋4mn2－2mn＋6m2n＋3mn.
解：原式＝(5－1)m＋(2－3)n＝4m－n.
解：原式＝(3－1)a2＋(－2＋3)a＋(－1－5)＝2a2＋a－6.
解：原式＝(－5＋6)m2n＋4mn2＋(－2＋3)mn＝m2n＋4mn2＋mn.
4.求多项式4x2+2xy+9y2-2x2-3xy+y2的值，其中x=2，y=1.解：4x2+2xy+9y2-2x2-3xy+y2 =(4-2)x2+(2-3)xy+(9+1)y2 =2x2-xy+10y2. 当x=2，y=1时, 原式=2×22-2×1+10×12=8-2+10=16.
5.求下列多项式的值：7x2-3x2-2x-2x2+5+6x，其中x=-2；5a-2b+3b-4a-1，其中a=-1， b=2.
（1）解：7x2-3x2-2x-2x2+5+6x
=7x2-3x2-2x2-2x+6x+5
当x=-2时，原式=2×(-2)2+4×(-2)+5=5
（2）解： 5a-2b+3b-4a-1
=5a-4a-2b+3b-1
当a=-1， b=2时，原式=-1+2-1=0
1.法则：把同类项的系数相加，所得的结果作为系数，字母和字 母的指数保持不变.
2.合并同类项的依据是乘法分配律的逆用.
3.如果两个同类项的系数互为相反数，合并同类项后，结果为0.
4.合并同类项的步骤：（1）“找”出同类项，作标记.（2）利用法则，把同类项的系数相加，字母和字母的指数不变.（3）写出合并后的结果.