2025高考数学一轮复习-6.2.1排列-6.2.2排列数【课件】

这是一份2025高考数学一轮复习-6.2.1排列-6.2.2排列数【课件】，共23页。
1 |排列、排列数与排列数公式 
1.从n个不同元素中取出m(m≤n)个元素,并按照①　一定的顺序    排成一列,叫做 从n个不同元素中取出m个元素的一个排列. 2.从n个不同元素中取出m(m≤n)个元素的所有不同排列的②　个数    ,叫做从n个 不同元素中取出m个元素的排列数,用符号③         表示.3.排列数公式: =④    n(n-1)(n-2)…(n-m+1)    (m,n∈N*,m≤n).
2 |全排列、阶乘的概念及相关结论
1.把n个不同的元素⑤　全部取出    的一个排列,叫做n个元素的一个全排列,记作 ⑥         .2.正整数1到n的连乘积,叫做n的阶乘,用⑦    n!    表示.3.阶乘的相关结论(1)规定:0!=⑧　1    .(2) =⑨    n!    (n∈N*).(3)排列数公式的另一种形式: =⑩         (m,n∈N*,m≤n).
3 |处理排列问题的常用方法
对于排列问题,从解题途径上看有直接法和间接法.从解题策略上看,有元素分析法和位置分析法.从解题技巧上看,有捆绑法和插空法.
1.若组成两个排列的元素相同,则这两个排列是相同的. (    ✕　)组成两个排列的元素的排列顺序不相同时,这两个排列是不相同的.2.a,b,c与b,a,c是同一个排列. (    ✕　)3.排列数公式 = 中m≠n. (    ✕　)4.4×5×6×…×(n-1)×n= ,其中n∈N*,n≥4. (　√　)5.5个人站成一排,其中甲、乙两人不相邻的排法可列式为 -  . (　√　)利用插空法可列式为  ;利用间接法可列式为 -  .
判断正误,正确的画“√”,错误的画“✕”.
 1.“排列”与“排列数”是两个不同的概念.排列是指“从n个不同元素中取出m (m≤n)个元素,并按照一定的顺序排成一列”,这不是一个数;排列数是指“从n个不 同元素中取出m(m≤n)个元素的所有不同排列的个数”,这是一个数.2.规定:0!=1,不按阶乘的含义作解释.在排列数公式 =n(n-1)…(n-m+1)中,n,m要满足的条件是n,m∈N*,m≤n.3.排列数的性质: =n =m + .
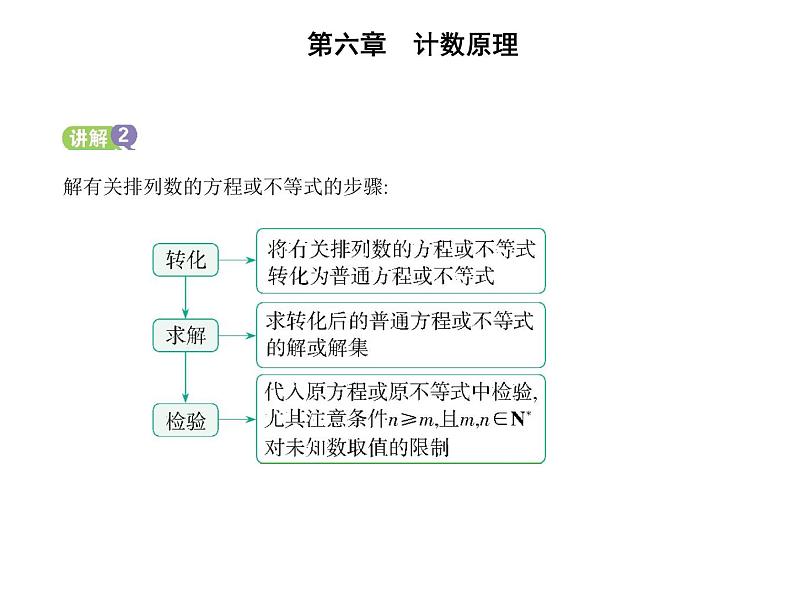
 解有关排列数的方程或不等式的步骤:
(1)用排列数表示(55-n)(56-n)…(69-n)(n∈N*且n6 .
解析    (1)∵55-n,56-n,…,69-n中最大的数为69-n,且共有(69-n)-(55-n)+1=15个正整 数,∴(55-n)(56-n)…(69-n)= .(2) = = =3.(3)①原式=(2!-1)+(3!-2!)+(4!-3!)+…+[(n+1)!-n!]=(n+1)!-1.②∵ = - ,∴ + + +…+ = + + +…+ =1- .
(4)易知 ∴2 ,其中26,即x2-21x+104>0,∴(x-8)(x-13)>0,解得x13.∵2