华东师大版（2024）八年级上册第12章 整式的乘除12.2 整式的乘法3 多项式与多项式相乘完美版ppt课件

这是一份华东师大版（2024）八年级上册第12章 整式的乘除12.2 整式的乘法3 多项式与多项式相乘完美版ppt课件，共17页。PPT课件主要包含了教学目标，新知导入，新知讲解，例题讲解，x2-2x-35，4m2-9n2，巩固练习，典例讲解，课堂总结，x2+7x+3等内容，欢迎下载使用。

1.能说出多项式与多项式相乘的法则，并且知道多项式乘以多项式的结果仍然是多项式.会进行多项式乘以多项式的计算及混合运算. 2.培养学生灵活运用所学知识分析问题、解决问题的能力. 3.培养独立思考、主动探索的习惯和初步解决问题的愿望及能力.
【教学重点】掌握多项式乘以多项式的法则.【教学难点】运用法则进行混合运算时，不要漏项.
某地区在退耕还林期间，将一块长m米、宽a米的长方形林地的长、宽分别增加n米和b米.用两种方法表示这块林地现在的面积，你知道下面的等式蕴含着什么样的运算法则吗？
(m+n)(a+b) =ma+mb+na+nb
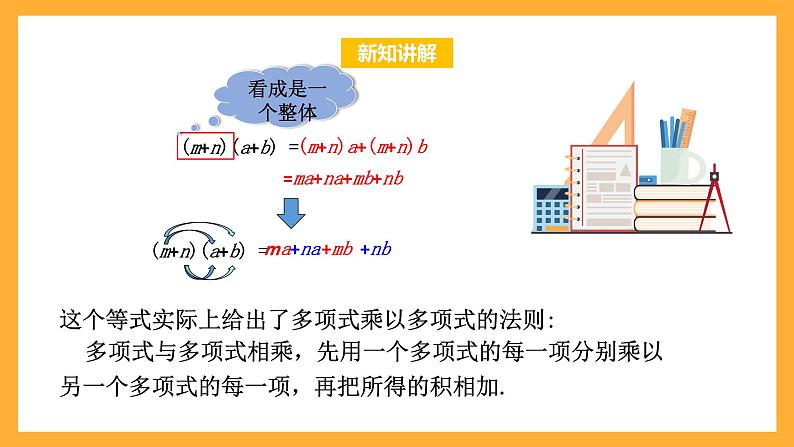
(m+n)(a+b) =
(m+n)a+(m+n)b
=ma+na+mb+nb
+na +nb
ma +mb
这个等式实际上给出了多项式乘以多项式的法则: 多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加.
例1 计算:(1) (x+2)(x-3) ;(2) (2x+5y)(3x-2y).
解:(1) (x+2)(x-3)=x2-3x+2x-6=x2-x-6. (2) (2x+5y)(3x-2y)= 6x2-4xy+15yx-10y2= 6x2+11xy-10y2
例2 计算:(1) (m-2n)(m2+mn -3n2); (2) (3x2-2x+2)(2x+1).
解：(1)(m-2n)(m2+mn -3n2); =m·m2+m·mn-m·3n2-2n·m2 -2n·mn+2n·3n2 = m3+m2n-3mn2-2m2n-2mn2+6n3 = m3-m2n - 5mn2+ 6n3
解：(2) (3x2-2x+2)(2x+1).=6x3+3x2-4x2-2x+4x+2=6x3-x2+2x+2.
解题策略 注意不要漏乘，尤其是含有常数的一项，结果最后要化为最简。
（1）(x+5)(x-7)；
（2）(x+5y)(x-7y)；
（3）(2m+3n)(2m-3n)；
（4）(2a+3b)2.
=x2-7x+5x-35
=x2-7xy+5xy-35y2
=x2-2xy-35y2
=4m2+6mn-6mn-9n2
=4a2+12ab+9b2
解题策略 不含某项，即化简、合并以后该项的系数为0
多项式乘以多项式，展开后项数很有规律，在合并同类项之前，展开式的项数恰好等于两个多项式的项数的积.
多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加.
1、算一算: (1) (2x+1)(x+3) (2) (m+2n)(m+3n) (3) (a-1)2 (4) (a+3b)(a–3b)
(5) (x+2)(x+3) (6) (x-4)(x+1) (7) (y+4)(y-2) (8) (y-5)(y-3)
3、通过计算，比较图①和图②中的阴影部分的面积，可以验证的算式是（ ）