


初中数学华东师大版(2024)八年级上册4 角边角试讲课课件ppt
展开1、掌握判定两个三角形全等,会用、、、判定三角形全等. 2、会用判定两个三角形全等.(重点) 3、证明全等时,判定方法的选择.(难点)
问题:目前我们已经学习了几种三角形全等的判定方法?
有两边和它们的夹角对应相等的两个三角形全等
有两角和它们的夹边对应相等的两个三角形全等
有两角和其中一角的对边对应相等的两个三角形全等
如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗?
不一定,如下面的两个三角形就不全等。
如果将上面的三个角换成三条边,结果又如何呢?
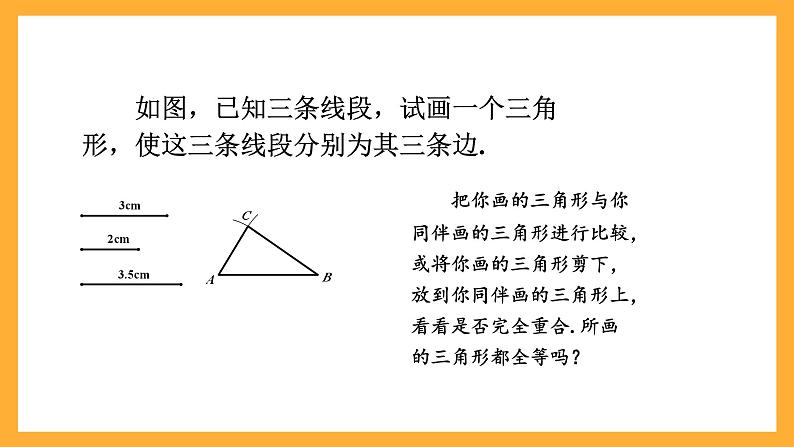
如图,已知三条线段,试画一个三角形,使这三条线段分别为其三条边.
把你画的三角形与你同伴画的三角形进行比较,或将你画的三角形剪下,放到你同伴画的三角形上,看看是否完全重合. 所画的三角形都全等吗?
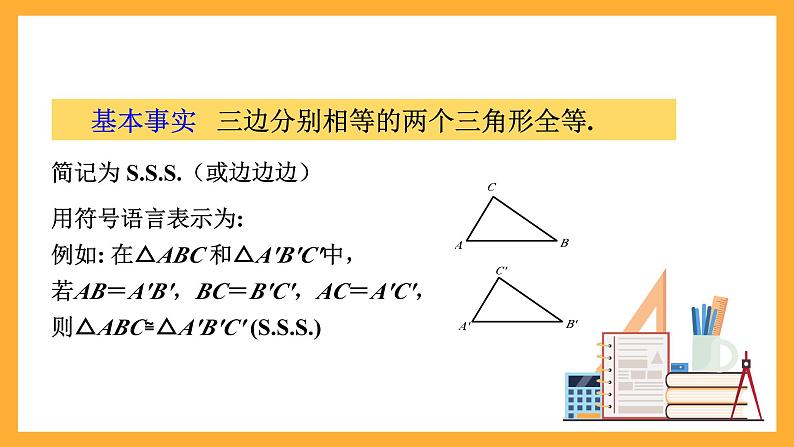
基本事实 三边分别相等的两个三角形全等.
用符号语言表示为:例如: 在△ABC 和△A′B′C′中,若AB=A′B′,BC=B′C′,AC=A′C′,则△ABC≌△A′B′C′ ()
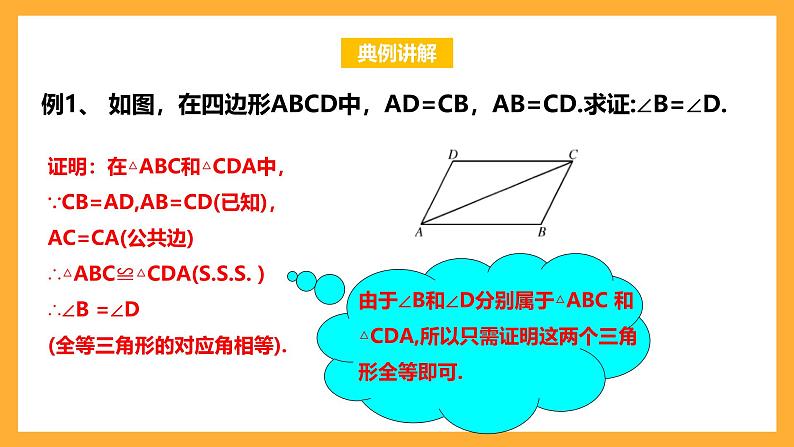
例1、 如图,在四边形ABCD中,AD=CB,AB=CD.求证:∠B=∠D.
由于∠B和∠D分别属于△ABC 和△CDA,所以只需证明这两个三角形全等即可.
证明:在△ABC和△CDA中,∵CB=AD,AB=CD(已知),AC=CA(公共边)∴△ABC≌△CDA( )∴∠B =∠D(全等三角形的对应角相等).
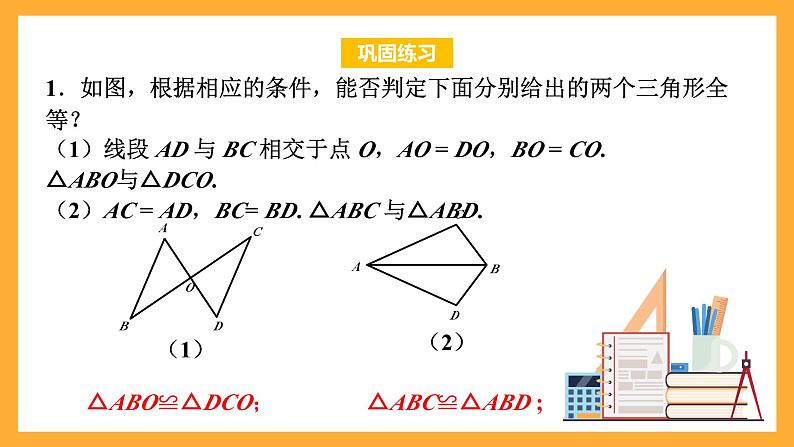
1.如图,根据相应的条件,能否判定下面分别给出的两个三角形全等?(1)线段 AD 与 BC 相交于点 O,AO = DO,BO = CO. △ABO与△DCO.(2)AC = AD,BC= BD. △ABC 与△ABD.
△ABC≌△ABD ;
2.如图,已知 AB = DC, AC = DB. 求证:△ABC≌△DCB.
证明:在△ABC 和△DCB 中,∵AB=DC,AC=DB,BC=CB,∴△ABC≌△DCB ().
3. 如图,点 B、E、C、F 在同一条直线上,AB = DE,AC = DF , BE = CF.求证:∠A = ∠D.并找出图中相互平行的线段,说明 你的理由.
证明:∵BE=CF,∴BE+CE=FC+EC,∴BC=EF.在△ABC 和△DEF 中,∵AB=DE,AC=DF,BC=EF,∴△ABC≌△DEF (),∴∠A =∠D .AC∥DF.因为∠ACB=∠DFE,所以AC∥DF.AB∥DE.因为∠B=∠DEF,所以 AB∥DE.
至此,我们已经学习了关于全等三角形的三个基本事实,这是进行演绎推理的重要依据. 它们是从静态的角度探索发现的判定方法,其本质与动态的全等三角形定义是一致的,即在这些条件下,两个三角形一定可以通过图形的基本变换 (轴对称、平移与旋转) 而相互重合.
我们可以将前面关于全等三角形判定的探索得到的结论归纳成下表(请补充完整表格中的内容):
例2、 如图,AB=CD,BC=DA,点E、F在AC上,且AE=CF求证:DE=BF.(方法的综合选择,一题多解)
4. 如图,在△ABC和△A’B’C’中,点D和点D’分别是BC和B’C’的中点,且AB=A’B’,BC=B’C’,AD=A’D’求证:△ABC≌△A’B’C’
三边分别相等的两个三角形全等
三角形全等的判定方法的综合应用
1.如图,要使各对三角形全等,还需要增加什么条件?(1)∠A =∠D,∠B = ∠F ; (2)∠A =∠D,AB = DE.
解: (1)AB=DF (或AC=DE 或 BC=FE);(2)∠B=∠E (或∠C=∠F 或 AC=DF).
2. 如图,已知 AB 与 CD 相交于点 O,∠A = ∠D, CO = BO. 求证:△AOC≌△DOB.
证明: 在△AOC 和△DOB 中,∵∠A =∠D ,∠AOC=∠DOB,CO=BO,∴△AOC≌△DOB ()
3. 如图,∠1 = ∠2,∠3 =∠4 . 求证: AB = AC.
证明: ∵∠3=∠4,∴∠ADC=∠ADB.在△ADC 和△ADB 中,∵∠1=∠2,AD =AD,∠ADC=∠ADB,∴△ADC≌△ADB (),∴AB = AC.
数学八年级上册5 边边边课前预习课件ppt: 这是一份数学八年级上册<a href="/sx/tb_c94177_t3/?tag_id=26" target="_blank">5 边边边课前预习课件ppt</a>,共24页。PPT课件主要包含了温故知新,SAS,ASA,AAS,△ABC即为所求,做一做,“边边边”判定方法,几何语言,1已知两边,2已知一边一角等内容,欢迎下载使用。
初中数学华师大版八年级上册5 边边边教学演示课件ppt: 这是一份初中数学华师大版八年级上册5 边边边教学演示课件ppt,共16页。PPT课件主要包含了创设情境引入新课,问题三,探究新知,归纳总结,学以致用,巩固提高练习,拓展延伸练习提升等内容,欢迎下载使用。
八年级上册5 边边边课文ppt课件: 这是一份八年级上册5 边边边课文ppt课件,文件包含5边边边pptx、5边边边doc等2份课件配套教学资源,其中PPT共25页, 欢迎下载使用。













