




所属成套资源:教科版(2019)高一信息技术必修一 同步课件+教案
高中信息技术教科版 (2019)必修1 数据与计算4.2 数值计算完美版课件ppt
展开这是一份高中信息技术教科版 (2019)必修1 数据与计算4.2 数值计算完美版课件ppt,共27页。PPT课件主要包含了函数的定义和调用,如何使用呢,完善代码,尝试运行,练习任务,运行程序等内容,欢迎下载使用。
感受数据的图形化表示设计解析式或迭代方程,进行数值计算,解决问题。了解数值类算法在实际问题解决时的应用及常用方法。
imprt matha=int(input ("请输入底数:"))x=int(input ("请输入指数:") )def zhishu(a1,x1): y=math.pw(a1,x1) return yprint(a, x, zhishu(a, x))
提示:导入了math库,在math库了涵盖了常用数学函数。pw即指数函数。
【任务一 绘制数学函数曲线】
活动1 用wps绘制正弦曲线——描点法
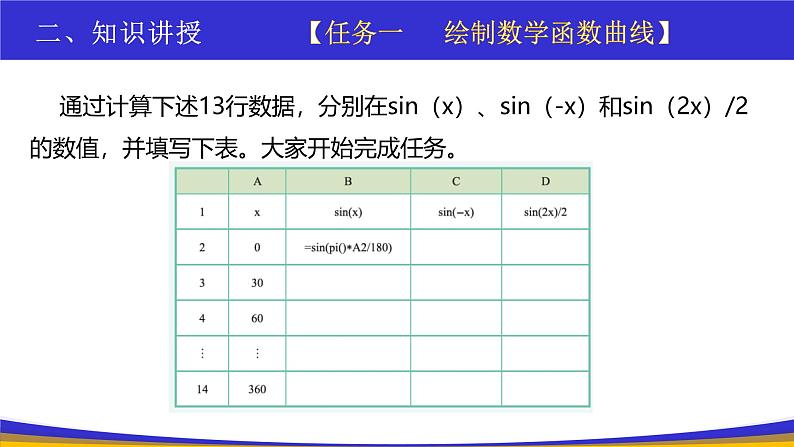
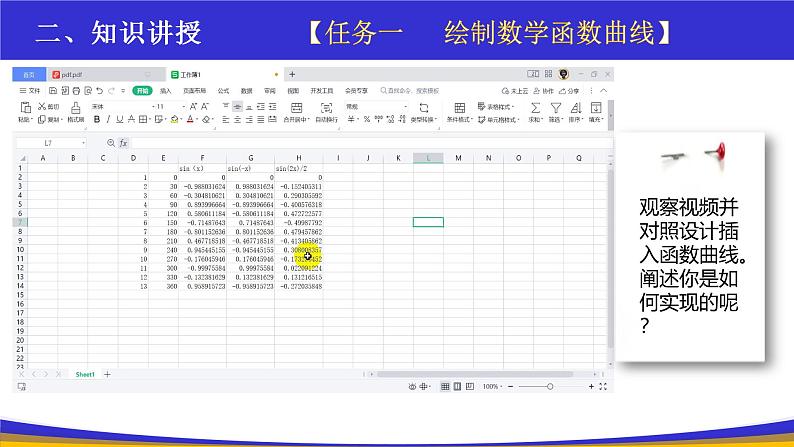
利用平时使用的电子表格软件就能绘制函数图像。方法如下:若以30°为间隔,绘制0~360°之间的正弦函数图像,则首先需要在WPS 中完成下列表格数据的计算。
用描点法画函数图像一般分三步:首先建立平面直角坐标系其次根据解析式计算出若干点的坐标并画在坐标系内最后将这些点依次连接起来
通过计算下述13行数据,分别在sin(x)、sin(-x)和sin(2x)/2的数值,并填写下表。大家开始完成任务。
活动2 用Pythn绘制正弦曲线
查阅资料,并自主学习numpy模块和matpltlib模块。用Pythn绘制正弦曲线。
numpy模块简介numpy是一个科学计算包,其中包含很多数学函数,如三角函数、矩阵计算方法等。通过该模块中的arange函数可以创建一个等差数列。如在0~2π之间每隔0.01取个值,则可以用arange(0,2*numpy. pi,0.01)来表示,其中numpy.pi表示π。下列代码可以产生sin(x)的若干个关键点。matpltlib模块简介matpltlib模块是Pythn中最出色的绘图库,功能很完善。调用matpltlib.pyplt时,坐标系可以根据数值范围自动生成。matpltlib的绘图原理很简单,利用plt画线函数就可以在直角平面内轻松地将(x,y)坐标点对连接成平滑曲线。例如:在上述代码的适当位置增加下列语句,就可以将刚才生成的关键点连接起来。
#加载numpy模块并取一个简洁的别名为np,便于后续引用imprt numpy as np#x在0到2π之间,每隔0.01取一个点x=np.arange(0,2*np.pi,0.01)y=np.sin(x)#通过解析式计算列表x对应的列表y的值
#加载matpltlib.pyplt并取别名为plt imprt matpltlib.pyplt as plt#将点对连线plt.plt(x,y)#将绘制的图像窗口显示出来plt.shw()
_________________#加载numpy模块并取别名为np#加载matpltlib.pyplt并取别名为plt imprt matpltlib.pyplt as plt_________________#列表x在0到2π之间,每隔0.01取一个点_________________#求sin(x)对应的列表y1的值y2=np.sin(-x)#求sin(-x)对应的列表y2的值_________________#求sin(2x)/2对应的列表y3的值_________________#绘制sin(x)的图像plt.plt(x,y1)
_________________#绘制sin(-x)的图像_________________#绘制sin(2x)/2的图像#设置图像标题plt.title('sin(x)')#设置X轴标题plt.xlabel('×')#设置Y轴标题plt.ylabel('Y')#将绘制的函数图像窗口显示出来plt.shw()
imprt numpy as np#加载numpy模块并取别名为np#加载matpltlib.pyplt并取别名为plt imprt matpltlib.pyplt as pltx=np.arange(0,2*np.pi,0.01)#列表x在0到2π之间,每隔0.01取一个点y1=np.sin(x)#求sin(x)对应的列表y1的值y2=np.sin(-x)#求sin(-x)对应的列表y2的值y3=np.sin(2*x)/2#求sin(2x)/2对应的列表y3的值plt.plt(x,y1)#绘制sin(x)的图像plt.plt(x,y1)plt.plt(x,y2)plt.plt(x,y3)
#设置图像标题plt.title('sin(x) || sin(-x) || sin(2x)/2')#设置X轴标题plt.xlabel('×')#设置Y轴标题plt.ylabel('Y')#将绘制的函数图像窗口显示出来#显示三个函数的图例标题#legend = plt.legend(['sin(x)','sin(-x)','sin(2x)/2'])plt.shw()
#显示三个函数的图例标题legend = plt.legend(['sin(x)','sin(-x)','sin(2x)/2'])
查找资料并在该图基础上绘制添加每个函数的图例标题。
对比wps绘制的函数图像与Pythn绘制函数图像的优劣
wps绘制图像需要多行数据,且精度不够,图像不光滑。但wps简单易理解。Pythn绘制图像需要导入相应函数库和图像库,结合库函数实现图形绘制,较为复杂,但是图形平滑美观。
【任务二 求解斐波那契数列】
斐波那契数列(Fibnacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Lenardda Fibnacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1,1,2,3,5,8,13······
1、这个数列从第3项开始,每一项都等于前两项之和。2、斐波那契数的边界条件是:f1,f2,f1+f2,fn=f(n-1)+f(n-2)
【分析斐波那契数列算法】
利用迭代算法解决问题,有三个关键步骤:(1)确定迭代变量,如活动2中的fl、f2;(2)建立迭代关系式;(3)对迭代过程进行控制
请根据示意图完善下列程序代码。def fib(n):#利用迭代求斐波那契数列的第n个数f2=f1=1 #第1个月、第2个月初值设定fr i in range(3,n+1): #推算从第三个月开始,并且至n+1个月结束f1,f2=f2,f1+f2 return f2n=int(input('输入需要计算的月份数:')#输出最终解print('兔子总对数为:',fib(n))
查找资料,小组合作完成利用Pythn实现递归方法下的斐波那契数列图象绘制。并解释核心代码实现过程。
活动2 用Pythn绘制斐波那契数列图象
frm turtle imprt *#输入自定义数列的个数amunt=int(input("请输入斐波那契数列的而个数,推荐15:"))#数列产生a1=0a2=1tem_he=0shulie=[]fr i in range(1,amunt): #终端输出数列的数值 print(a1,end=',') tem_he=a1+a2 a1=a2 a2=tem_he #数列添加数值 shulie.append(tem_he)
#turtle画图fr i in range(1,amunt-1): fr n in range(4): frward(shulie[i]) left(90) #画圆circle(shulie[i],90)#输出数列数值write(shulie[i],fnt=("微软雅黑",i*2))
相关课件
这是一份信息技术必修1 数据与计算4.2 数值计算图文课件ppt,共22页。PPT课件主要包含了学习目标,numpy模块简介,巩固提升等内容,欢迎下载使用。
这是一份教科版 (2019)必修1 数据与计算4.2 数值计算优秀ppt课件,共16页。PPT课件主要包含了学习目标,温故而知新,使用电子表格求解,迭代法,课堂练习,巩固提升,课堂小结等内容,欢迎下载使用。
这是一份教科版 (2019)必修1 数据与计算4.2 数值计算一等奖课件ppt,共17页。PPT课件主要包含了学习目标,numpy模块简介,课堂练习,巩固提升,课堂小结等内容,欢迎下载使用。













