





还剩14页未读,
继续阅读
沪科版2020上海高二物理选修一 专题五动量、动力学和能量观点在力学中的应用(课件)
展开
这是一份沪科版2020上海高二物理选修一 专题五动量、动力学和能量观点在力学中的应用(课件),共22页。
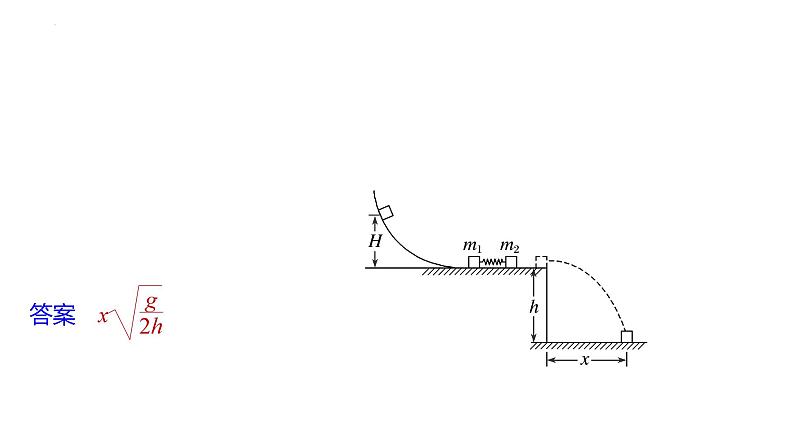
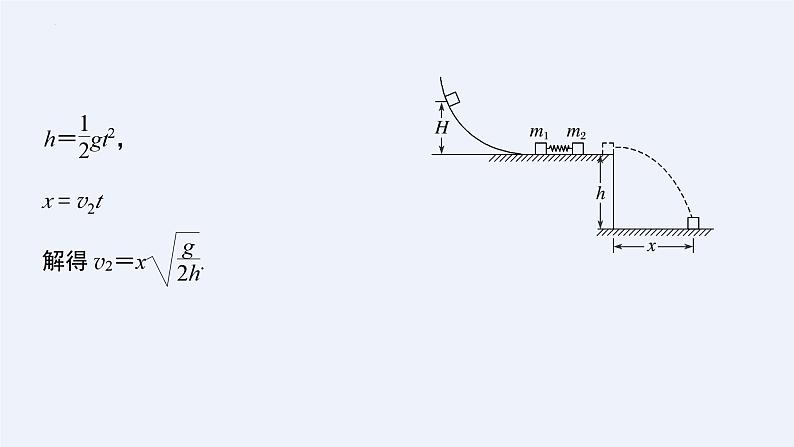
第一章 动量专题五 动量、动力学和能量观点在力学中的应用【学习目标】1.进一步熟悉牛顿第二定律、动能定理、动量守恒定律、能量 守恒定律等规律.2.灵活运用动力学观点、动量观点和能量观点解决力学问题.一、力的三个作用效果与五个规律二、选用力学规律的原则1.如果要列出各物理量在某一时刻的关系式,可用牛顿第二定律.2.研究某一物体受到力的持续作用发生运动状态改变时,一般用动量定理(涉及时间的问题)或动能定理(涉及位移的问题)去解决问题.3.若研究的对象为一物体系统,且它们之间有相互作用,一般用两个守恒定律解决问题,但需注意所研究的问题是否满足守恒的条件.4.在涉及相对位移问题时优先考虑利用能量守恒定律求解,根据系统克服摩擦力所做的总功等于系统机械能的减少量(即转化为系统内能的量)列方程.5.在涉及碰撞、爆炸、打击、绳绷紧等物理现象时,需注意到这些过程一般隐含有系统机械能与其他形式能量之间的转化,这种问题由于作用时间极短,因此动量守恒定律一般能派上大用场.例1 如图所示,较长的曲面与水平桌面平滑连接,将m1、m2之间的轻弹簧压缩后用细线连接,静置于水平桌面上,弹簧与两物体不拴连.现将细线烧断,弹簧将两物体弹开,m2离开弹簧后从右边飞出,m1冲上曲面.已知桌面高为h,m2平抛的水平射程为x,m1=2m,m2=m,不计一切摩擦,重力加速度为g,求:(1)m2离开弹簧时的速度大小;解析 对m2平抛过程分析,有x=v2t(2)m1上升到曲面最高点时距桌面的高度H;解析 弹簧将两物体弹开的过程,m1、m2组成的系统动量守恒,取向左为正方向,由动量守恒定律有m1v1-m2v2=0对m1冲上曲面过程,由机械能守恒定律有(3)弹簧的最大弹性势能.(1)灵活选取系统.根据题目的特点可选取其中动量守恒或能量守恒的几个物体为研究对象,不一定选所有的物体为研究对象.(2)灵活选取物理过程.在综合题目中,物体运动常有几个不同的过程,根据题目的已知、未知条件灵活地选取物理过程来研究.列方程前要注意分析、判断所选过程动量、能量的守恒情况.归纳总结例2 如图,光滑的水平地面上静止放置一辆小车A,质量mA=5 kg,上表面光滑,可视为质点的物块B置于A的最右端,B的质量mB=3 kg.现对A施加一个水平向右的恒力F=10 N,A运动一段时间后,小车左端固定的挡板与B发生碰撞,碰撞时间极短,碰后A、B粘合在一起,共同在F的作用下继续运动,碰撞后经时间t=0.8 s,二者的速度达到vt=2 m/s.求:(1)A开始运动时加速度a的大小;答案 2.0 m/s2解析 以A为研究对象,由牛顿第二定律有F=mAa(2)A、B碰撞后瞬间的共同速度v的大小;答案 1 m/s解析 A、B碰撞后一起在F的作用下运动时间t的过程中,由动量定理得Ft=(mA+mB)vt-(mA+mB)v代入数据解得v=1 m/s(3)A的上表面长度l.答案 0.64 m解析 设A、B发生碰撞前,A的速度为vA,对A、B发生碰撞的过程,由动量守恒定律有mAvA=(mA+mB)vA从开始运动到与B发生碰撞前,由动能定理有代入数据可得l=0.64 m.返回SUITANGYANLIAN ZHUDIANLUOSHI课堂练习1.(力学三大观点的综合应用)如图甲所示,一质量为2 kg的物体受水平拉力F作用,在粗糙水平面上做加速直线运动时的a-t图像如图乙所示,t=0时其速度大小为2 m/s,滑动摩擦力大小恒为2 N,则A.在t=6 s的时刻,物体的速度为 18 m/sB.在0~6 s时间内,合力对物体做 的功为400 JC.在0~6 s时间内,拉力对物体的 冲量为35 N·sD.在t=6 s的时刻,拉力F的功率为200 W12√12解析 类比速度—时间图像中位移的表示方法可知,速度变化量在加速度—时间图像中由a-t图线与t坐标轴所围面积表示,在0~6 s内Δv=18 m/s,v0=2 m/s,则t=6 s时的速度v=20 m/s,A项错;由动能定理可知,0~6 s内,合力做的功为W= mv2- mv02=396 J,B项错;由动量定理可知,IF-Ff·t=mv-mv0,代入已知条件解得IF=48 N·s,C项错;由牛顿第二定律可知,6 s末F-Ff=ma,解得F=10 N,所以拉力的功率P=Fv=200 W,D项对.2.(力学三大观点的综合应用)如图所示,一水平轻弹簧右端固定在粗糙水平面右侧的竖直墙壁上,质量为M=2 kg的物块静止在水平面上的P点,质量为m=1 kg的小球用长l=0.9 m的轻绳悬挂在P点正上方的O点.现将小球拉至轻绳与竖直方向成60°角位置,静止释放.小球到达最低点时恰好与物块发生弹性正碰.碰后物块向右运动并压缩弹12簧,之后物块被弹回,刚好能回到P点.设小球与物块只碰撞一次,不计空气阻力,物块和小球均可视为质点,重力加速度取g=10 m/s2.求:(1)小球第一次摆到最低点与物块碰撞前瞬间对轻绳的拉力大小;12答案 20 N又由牛顿第三定律有小球对轻绳的拉力FT′=FT解得:FT′=20 N.(2)弹簧的最大弹性势能Ep.12答案 2 J解析 小球与物块发生弹性碰撞,由动量守恒定律和能量守恒定律得:mv0=mv0′+Mv1小球反弹后回到P点的过程,又有:Ep=Q联立解得:Ep=2 J.返回
第一章 动量专题五 动量、动力学和能量观点在力学中的应用【学习目标】1.进一步熟悉牛顿第二定律、动能定理、动量守恒定律、能量 守恒定律等规律.2.灵活运用动力学观点、动量观点和能量观点解决力学问题.一、力的三个作用效果与五个规律二、选用力学规律的原则1.如果要列出各物理量在某一时刻的关系式,可用牛顿第二定律.2.研究某一物体受到力的持续作用发生运动状态改变时,一般用动量定理(涉及时间的问题)或动能定理(涉及位移的问题)去解决问题.3.若研究的对象为一物体系统,且它们之间有相互作用,一般用两个守恒定律解决问题,但需注意所研究的问题是否满足守恒的条件.4.在涉及相对位移问题时优先考虑利用能量守恒定律求解,根据系统克服摩擦力所做的总功等于系统机械能的减少量(即转化为系统内能的量)列方程.5.在涉及碰撞、爆炸、打击、绳绷紧等物理现象时,需注意到这些过程一般隐含有系统机械能与其他形式能量之间的转化,这种问题由于作用时间极短,因此动量守恒定律一般能派上大用场.例1 如图所示,较长的曲面与水平桌面平滑连接,将m1、m2之间的轻弹簧压缩后用细线连接,静置于水平桌面上,弹簧与两物体不拴连.现将细线烧断,弹簧将两物体弹开,m2离开弹簧后从右边飞出,m1冲上曲面.已知桌面高为h,m2平抛的水平射程为x,m1=2m,m2=m,不计一切摩擦,重力加速度为g,求:(1)m2离开弹簧时的速度大小;解析 对m2平抛过程分析,有x=v2t(2)m1上升到曲面最高点时距桌面的高度H;解析 弹簧将两物体弹开的过程,m1、m2组成的系统动量守恒,取向左为正方向,由动量守恒定律有m1v1-m2v2=0对m1冲上曲面过程,由机械能守恒定律有(3)弹簧的最大弹性势能.(1)灵活选取系统.根据题目的特点可选取其中动量守恒或能量守恒的几个物体为研究对象,不一定选所有的物体为研究对象.(2)灵活选取物理过程.在综合题目中,物体运动常有几个不同的过程,根据题目的已知、未知条件灵活地选取物理过程来研究.列方程前要注意分析、判断所选过程动量、能量的守恒情况.归纳总结例2 如图,光滑的水平地面上静止放置一辆小车A,质量mA=5 kg,上表面光滑,可视为质点的物块B置于A的最右端,B的质量mB=3 kg.现对A施加一个水平向右的恒力F=10 N,A运动一段时间后,小车左端固定的挡板与B发生碰撞,碰撞时间极短,碰后A、B粘合在一起,共同在F的作用下继续运动,碰撞后经时间t=0.8 s,二者的速度达到vt=2 m/s.求:(1)A开始运动时加速度a的大小;答案 2.0 m/s2解析 以A为研究对象,由牛顿第二定律有F=mAa(2)A、B碰撞后瞬间的共同速度v的大小;答案 1 m/s解析 A、B碰撞后一起在F的作用下运动时间t的过程中,由动量定理得Ft=(mA+mB)vt-(mA+mB)v代入数据解得v=1 m/s(3)A的上表面长度l.答案 0.64 m解析 设A、B发生碰撞前,A的速度为vA,对A、B发生碰撞的过程,由动量守恒定律有mAvA=(mA+mB)vA从开始运动到与B发生碰撞前,由动能定理有代入数据可得l=0.64 m.返回SUITANGYANLIAN ZHUDIANLUOSHI课堂练习1.(力学三大观点的综合应用)如图甲所示,一质量为2 kg的物体受水平拉力F作用,在粗糙水平面上做加速直线运动时的a-t图像如图乙所示,t=0时其速度大小为2 m/s,滑动摩擦力大小恒为2 N,则A.在t=6 s的时刻,物体的速度为 18 m/sB.在0~6 s时间内,合力对物体做 的功为400 JC.在0~6 s时间内,拉力对物体的 冲量为35 N·sD.在t=6 s的时刻,拉力F的功率为200 W12√12解析 类比速度—时间图像中位移的表示方法可知,速度变化量在加速度—时间图像中由a-t图线与t坐标轴所围面积表示,在0~6 s内Δv=18 m/s,v0=2 m/s,则t=6 s时的速度v=20 m/s,A项错;由动能定理可知,0~6 s内,合力做的功为W= mv2- mv02=396 J,B项错;由动量定理可知,IF-Ff·t=mv-mv0,代入已知条件解得IF=48 N·s,C项错;由牛顿第二定律可知,6 s末F-Ff=ma,解得F=10 N,所以拉力的功率P=Fv=200 W,D项对.2.(力学三大观点的综合应用)如图所示,一水平轻弹簧右端固定在粗糙水平面右侧的竖直墙壁上,质量为M=2 kg的物块静止在水平面上的P点,质量为m=1 kg的小球用长l=0.9 m的轻绳悬挂在P点正上方的O点.现将小球拉至轻绳与竖直方向成60°角位置,静止释放.小球到达最低点时恰好与物块发生弹性正碰.碰后物块向右运动并压缩弹12簧,之后物块被弹回,刚好能回到P点.设小球与物块只碰撞一次,不计空气阻力,物块和小球均可视为质点,重力加速度取g=10 m/s2.求:(1)小球第一次摆到最低点与物块碰撞前瞬间对轻绳的拉力大小;12答案 20 N又由牛顿第三定律有小球对轻绳的拉力FT′=FT解得:FT′=20 N.(2)弹簧的最大弹性势能Ep.12答案 2 J解析 小球与物块发生弹性碰撞,由动量守恒定律和能量守恒定律得:mv0=mv0′+Mv1小球反弹后回到P点的过程,又有:Ep=Q联立解得:Ep=2 J.返回
相关资料
更多









