人教版（2024）七年级上册（2024）2.1 有理数的加法与减法优质课教学ppt课件

这是一份人教版（2024）七年级上册（2024）2.1 有理数的加法与减法优质课教学ppt课件，文件包含核心素养人教版数学七年级上册211有理数的加法第1课时有理数的加法法则教学课件pptx、核心素养人教版数学七年级上册211有理数的加法第1课时有理数的加法法则教学设计docx、核心素养人教版数学七年级上册211有理数的加法第1课时有理数的加法法则分层作业解析版docx、核心素养人教版数学七年级上册211有理数的加法第1课时有理数的加法法则分层作业原卷版docx等4份课件配套教学资源，其中PPT共40页， 欢迎下载使用。
1. 理解有理数加法法则的探究过程，掌握有理数加法的法则；2. 能利用有理数加法的法则进行简单的有理数加法运算.
在第一章中，我们把数的范围扩大到了有理数，根据小学阶段学习数的经验，接下来就要研究有理数的运算.本章我们将在上一章以及小学已学的数的运算的基础上，进一步学习有理数的运算，将数的运算推广到有理数范围内，从而初步感悟数系扩充的完整过程，并认识运算在数学中的价值及其在解决实际问题中的作用.
3. 根据上述问题，列算式回答 (1)小红两次一共前进了几米？ (2)北京的气温两天一共上升了多少度？
2. 说明下列用负数表示的量的实际意义： (1)小红第一次前进了5米，接着按同一方向又前进了-2米； (2)北京的气温第一天上升了3℃，第二天又上升了-1℃.
1. 下列各组数中，哪一个数的绝对值较大？ (1)5和3； (2)﹣5和3； (3)5和﹣3； (4)﹣5和﹣3.
数的范围扩大到有理数后，就要研究有理数的运算.我们先把小学学习的加法与减法运算推广到有理数范围内.
在小学，我们学过正数及0的加法运算，引入负数后，在有理数范围内怎样进行加法运算呢？
这一天北京的温差是：3﹣（﹣3）.
1. 北京冬季某一天的气温为﹣3～3℃. 这一天北京的温差是多少?
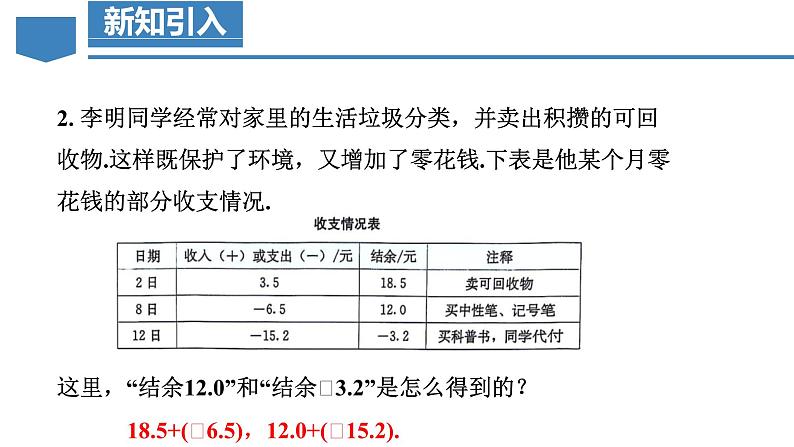
2. 李明同学经常对家里的生活垃圾分类，并卖出积攒的可回收物.这样既保护了环境，又增加了零花钱.下表是他某个月零花钱的部分收支情况.
18.5+(﹣6.5)，12.0+(﹣15.2).
这里，“结余12.0”和“结余﹣3.2”是怎么得到的？
要解决上面的问题，就要计算3﹣(﹣3)，18.5+(﹣6.5)，12.0+(﹣15.2).其实像这样的生活实际问题是无处不在，例如收入支出和盈利等问题也涉及了加法的运算，那么我们如何去处理这样的加法运算呢？我们以下面的例子并借助数轴来讨论有理数的加法.
思考：小学学过的加法运算涉及正数与正数相加、正数与0相加以及0与0相加.引入负数后，在有理数范围内，加法有哪几种情况？
借助具体情境和数轴来讨论有理数的加法.
思考：一个物体沿着一条直线做左右方向的运动，我们规定向右为正，向左为负.
－5 －4 －3 －2 －1 0 1 2 3 4 5
两次运动的最后结果是，物体从起点向右运动了8m，写成算式就是:
－1 －2 0 1 2 3 4 5 6 7 8
如果物体沿着一条直线先向右运动5m，再向右运动3m，那么两次运动的最后结果是什么?可以用怎样的算式表示？
(+5)+(+3)=+8.
简记为：5 + 3 = 8. ①
两次运动的最后结果是，物体从起点向左运动了8m，写成算式是:
如果物体沿着一条直线先向左运动5m，再向左运动3m，那么两次运动的最后结果是什么?可以用怎样的算式表示？
(﹣5)+(﹣3)=﹣8. ②
－8 －7 －6 －5 －4 －3 －2 －1 0 1 2
从算式①②可以看出：符号相同的两个数相加，和的符号不变，且和的绝对值等于加数的绝对值的和.
5 + 3 = 8. ①
(﹣5)+(﹣3)=﹣8. ②
如果物体沿着一条直线先向左运动3m，再向右运动5m，那么两次运动的最后结果是什么？如何用算式表示？
两次运动的最后结果是，物体从起点向右运动了2m，用算式表示是:
(﹣3)+(+5)=+2.
－5 －4 －3 －2 －1 0 1 2 3 4 5
简记为： (﹣3)+5=2. ③
－5 －4 －3 －2 －1 0 1 2 3 4 5
如果物体沿着一条直线先向右运动3m，再向左运动5m，那么两次运动的最后结果是什么？如何用算式表示？
用算式表示是：(+3)+(﹣5)=﹣2.
简记为： 3+(﹣5)=﹣2. ④
从算式③④可以看出：绝对值不相等、符号相反的两个数相加，和的符号与绝对值较大的加数的符号相同，且和的绝对值等于加数的绝对值中较大者与较小者的差.
(﹣3)+5=2. ③
3+(﹣5)=﹣2. ④
－5 －4 －3 －2 －1 0 1 2 3 4 5
如果物体沿着一条直线先向右运动5m，再向左运动5m，那么两次运动的最后结果是什么？如何用算式表示？
用算式表示为：(+5)+(﹣5)=0.
简记为： 5+(﹣5)=0. ⑤
算式⑤表明：互为相反数的两个数相加，结果为0.
5+(﹣5)=0. ⑤
－5 －4 －3 －2 －1 0 1 2 3 4 5
如果物体第1 s向右(或左)运动5m，第2 s原地不动，那么2 s后物体从起点向 运动了 m.
－5 －4 －3 －2 －1 0 1 2 3 4 5
用算式表示为： 5+0=5或(﹣5)+0=﹣5. ⑥
算式⑥表明：一个数与0相加，结果仍是这个数.
5+0=5或(﹣5)+0=﹣5. ⑥
(﹣5)+(﹣3)=﹣8.
异号两数相加(绝对值不相等)
异号两数相加(绝对值相等)
(﹣5)+0=﹣5. 5+0=5.
从算式可知，在有理数的加法运算中，既要考虑符号，又要考虑绝对值.
有理数加法的运算法则：1. 同号两数相加，和取相同的符号，且和的绝对值等于加数的绝对值的和.2. 绝对值不相等的异号两数相加，和取绝对值较大的加数的符号，且和的绝对值等于加数的绝对值中较大者与较小者的差. 互为相反数的两个数相加得0；3. 一个数与0相加，仍得这个数.
(﹣4) + (﹣8)=
(﹣9) + (+2)=
和取绝对值较大加数的符号
加数的绝对值中较大者与较小者的差
有理数加法运算的步骤：
1. 先判断加数的类型（同号、异号）； 2. 再确定和的符号：同号取相同的符号；异号取绝对值较大的加数的符号；3. 最后进行绝对值的加减运算.
解：（1）（-3）+（-9） = -(3+9) = -12
例1：计算：（1）（-3）+（-9）；（2）（-8）+0 ；（3）12+（-8）
有理数加法运算，先定符号，再算绝对值.
（两个加数同号，用加法法则的第1条计算）
（和取负号，把绝对值相加）
解：（2）（-8）+0 = -8
例1：计算：（1）（-3）+（-9）；（2）（-8）+0； （3）12+（-8）.
（3）12+（-8） =+（12-8） =4
（两个加数异号，用加法法则的第2条计算）
（和取正号，用大的绝对值减去小的绝对值）
解：（4）（-4.7）+ 3.9 = -(4.7-3.9) = -0.8
例1：计算：（4）（-4.7）+3.9；（5）（ ）+（+ ）
（和取负号，用大的绝对值减去小的绝对值）
（互为相反数的两个数相加）
任何一个数加上一个正数，和与原来的数有怎样的大小关系？加上一个负数呢？请你先借助数轴直观地得出结论，再利用有理数的加法法则进行说明.
例2：足球循环赛中，红队胜黄队4:1，黄队胜红队1:0，计算各队的净胜球数．
解：三场比赛中，红队共进4球，失2球，净胜球数为：(+4)+(-2)=+(4-2)=2；黄队共进2球，失4球，净胜球数为：(+2)+(-4)= -(4-2)= -2；蓝队共进1球，失1球，净胜球数为：(+1)+(-1)=0.
口算下列各题，并说明理由：(+3)+(+5)； (﹣3)+(﹣5)； (+3)+(﹣5)； (﹣3)+(+5)；(+4)+(﹣4)； (+9)+(﹣2)； (﹣9)+(+2)； (﹣9)+0.
1. 用“＞ ”或“＜”填空： ①如果a>0，b>0，那么a+b 0； ②如果a