2024-2025学年甘肃省张掖市甘州区数学九上开学预测试题【含答案】

这是一份2024-2025学年甘肃省张掖市甘州区数学九上开学预测试题【含答案】，共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
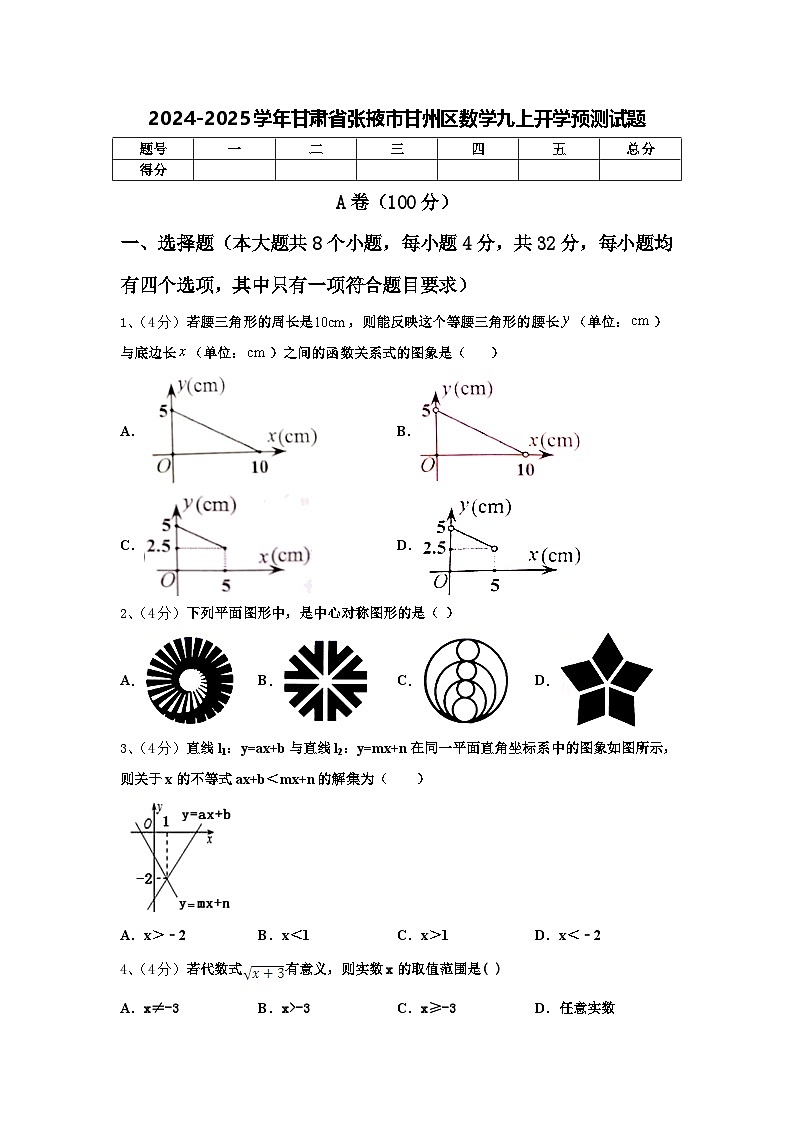
1、（4分）若腰三角形的周长是，则能反映这个等腰三角形的腰长（单位：）与底边长（单位：）之间的函数关系式的图象是（ ）
A．B．
C．D．
2、（4分）下列平面图形中，是中心对称图形的是（ ）
A．B．C．D．
3、（4分）直线l1：y=ax+b与直线l2：y=mx+n在同一平面直角坐标系中的图象如图所示，则关于x的不等式ax+b＜mx+n的解集为（ ）
A．x＞﹣2B．x＜1C．x＞1D．x＜﹣2
4、（4分）若代数式有意义，则实数x的取值范围是( )
A．x≠-3B．x>-3C．x≥-3D．任意实数
5、（4分）已知直线y＝kx＋b经过一、二、三象限，则直线y＝bx－k－2的图象只能是（ ）
A．B．C．D．
6、（4分）关于一次函数，下列结论正确的是
A．图象经过B．图象经过第一、二、三象限
C．y随x的增大而增大D．图象与y轴交于点
7、（4分）一天李师傅骑车上班途中因车发生故除，修车耽误了一段时间后继续骑行，按时赶到了单位，如图描述了他上班途中的情景，下列说法中错误的是（ ）
A．李师傅上班处距他家200米
B．李师傅路上耗时20分钟
C．修车后李师傅骑车速度是修车前的2倍
D．李师傅修车用了5分钟
8、（4分）函数中，自变量x的取值范围是（ ）
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，在△ABC中，∠CAB=70º，在同一平面内，将△ABC绕点逆时针旋转50º到△的位置，则∠= _________度.
10、（4分）函数：中，自变量x的取值范围是_____．
11、（4分）某班同学要测量学校升国旗的旗杆高度，在同一时刻，量得某同学的身高是1.5米，影长是1米，且旗杆的影长为8米，则旗杆的高度是 _________________ 米.
12、（4分）如图，△ABC中，∠C=90°，AD平分∠BAC交BC于点D，BD：DC=2：1，BC=7.8cm，则D到AB的距离为____cm．
13、（4分）设函数与的图象的交点坐标为，则的值为__________.
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，在平行四边形ABCD中，E，F为对角线BD上的两点，且∠DAE＝∠BCF．
求证：（1）AE＝CF；
（2）四边形AECF是平行四边形．
15、（8分）如图，已知中，，请用尺规作出AB边的高线请留作图痕迹，不写作法
16、（8分）某手机店销售部型和部型手机的利润为元，销售部型和部型手机的利润为元.
(1)求每部型手机和型手机的销售利润；
(2)该手机店计划一次购进，两种型号的手机共部，其中型手机的进货量不超过型手机的倍，设购进型手机部，这部手机的销售总利润为元.
①求关于的函数关系式；
②该手机店购进型、型手机各多少部，才能使销售总利润最大？
(3)在(2)的条件下，该手机店实际进货时，厂家对型手机出厂价下调元，且限定手机店最多购进型手机部，若手机店保持同种手机的售价不变，设计出使这部手机销售总利润最大的进货方案.
17、（10分）先化简，再求值：，其中x=，y=．
18、（10分）如图，在中，点在边上，点在边的延长线上，且，与交于点.
(1)求证：；
(2)若点是的中点，，求边的长.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）由作图可知直线与互相平行，则方程组的解的情况为______.
20、（4分）如图，菱形ABCD的对角线AC＝3cm，BD＝4cm，则菱形ABCD的面积是_____．
21、（4分）反比例函数y＝图象上有两个点（x1，y1），（x2，y2），其中0＜x1＜x2，则y1，y2的大小关系是_____（用“＜“连接）．
22、（4分）菱形中，，，以为边长作正方形，则点到的距离为_________．
23、（4分）若关于x的分式方程有增根，则k的值为__________.
二、解答题（本大题共3个小题，共30分）
24、（8分）为了满足市场需求，某厂家生产A、B两种款式的环保购物袋，每天共生产5000个，两种购物袋的成本和售价如下表：
设每天生产A种购物袋x个，每天共获利y元.
（1）求y与x的函数解析式；
（2）如果该厂每天最多投入成本12000元，那么每天最多获利多少元？
25、（10分）如图，已知AC⊥BC，BD⊥AD，AC 与BD 交于O，AC=BD．
求证：（1）BC=AD；
（2）△OAB是等腰三角形．
26、（12分）如图，Rt△ABO的顶点A是双曲线y1＝与直线y2＝－x-(k+1)在第二象限的交点.AB⊥x轴于B，且S△ABO＝．
（1）求这两个函数的解析式；
（2）求△AOC的面积．
（3）直接写出使y1＞y2成立的x的取值范围
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
根据三角形的周长列式并整理得到y与x的函数关系式，再根据三角形的任意两边之和大于第三边，任意两边之和大于第三边列式求出x的取值范围，即可得解．
【详解】
解：根据题意，x+2y=10，
所以，，
根据三角形的三边关系，x＞y-y=0，
x＜y+y=2y，
所以，x+x＜10，
解得x＜5，
所以，y与x的函数关系式为（0＜x＜5），
纵观各选项，只有D选项符合．
故选D．
本题主要考查的是三角形的三边关系，等腰三角形的性质，求出y与x的函数关系式是解答本题的关键.
2、B
【解析】
根据中心对称图形的概念求解．
【详解】
解：A、不是中心对称图形，故此选项错误；
B、是中心对称图形，故此选项正确；
C、不是中心对称图形，故此选项错误；
D、不是中心对称图形，故此选项错误．
故选B．
本题考查中心对称图形．
3、B
【解析】
由图象可以知道，当x=1时，两个函数的函数值是相等的，再根据函数的增减性可以判断出不等式ax+b＜mx+n解集．
【详解】
解：观察图象可知，当x＜1时，ax+b＜mx+n，
∴不等式ax+b＜mx+n的解集是x＜1
故选B．
本题考查了一次函数与一元一次不等式的关系，根据交点得到相应的解集是解决本题的关键．
4、C
【解析】
根据二次根式有意义的条件即可求出答案．
【详解】
∵代数式有意义
∴x+3≥0
∴x≥-3.
故选C.
本题考查二次根式有意义的条件，解题的关键是正确理解二次根式有意义的条件．
5、C
【解析】
由直线y＝kx＋b经过一、二、三象限可得出k＞0，b＞0，进而可得出−k−2＜0，再利用一次函数图象与系数的关系可得出直线y＝bx−k−2的图象经过第一、三、四象限．
【详解】
解：∵直线y＝kx＋b经过一、二、三象限，
∴k＞0，b＞0，
∴−k−2＜0，
∴直线y＝bx−k−2的图象经过第一、三、四象限．
故选：C．
本题考查了一次函数图象与系数的关系，牢记“k＞0，b＞0时，y＝kx＋b的图象在一、二、三象限；k＞0，b＜0时，y＝kx＋b的图象在一、三、四象限”是解题的关键．
6、D
【解析】
根据一次函数的性质，依次分析各个选项，选出正确的选项即可．
【详解】
A．把x=3代入y=﹣2x+3得：y=﹣6+3=﹣3，即A选项错误；
B．一次函数y=﹣2x+3的图象经过第一、二、四象限，即B选项错误；
C．一次函数y=﹣2x+3的图象上的点y随x的增大而减小，即C选项错误；
D．把x=0代入y=﹣2x+3得：y=3，图象与y轴交于点（0，3），即D选项正确．
故选D．
本题考查了一次函数图象上点的坐标特征和一次函数的性质，正确掌握一次函数的性质是解题的关键．
7、A
【解析】
观察图象，明确每一段小明行驶的路程，时间，作出判断．
【详解】
A．李师傅上班处距他家2000米，此选项错误；
B．李师傅路上耗时20分钟，此选项正确；
C．修车后李师傅骑车速度是=200米/分钟，修车前速度为=100米/分钟，∴修车后李师傅骑车速度是修车前的2倍，此选项正确；
D．李师傅修车用了5分钟，此选项正确．
故选A．
本题考查了学生从图象中读取信息的能力，同学们要注意分析其中的“关键点”，还要善于分析各图象的变化趋势．
8、B
【解析】
根据被开方数大于等于0列式进行计算即可得解．
【详解】
根据题意得，x+3⩾0，
解得x⩾−3.
故选B.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、10
【解析】
根据旋转的性质找到对应点、对应角进行解答．
【详解】
∵△ABC绕点A逆时针旋转50°得到△AB′C′，
∴∠BAB′=50°，
又∵∠BAC=70°，
∴∠CAB′=∠BAC-∠BAB′=1°．
故答案是：1．
本题考查旋转的性质：旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变．要注意旋转的三要素：①定点--旋转中心；②旋转方向；③旋转角度．
10、
【解析】
求函数自变量的取值范围，就是求函数解析式有意义的条件，根据分式分母不为0的条件，要使在实数范围内有意义，必须，即.
11、1．
【解析】
在同一时刻，物体的实际高度和影长成比例，据此列方程即可解答．
【详解】
解：设旗杆高度为x，则
，
解得x=1．
故答案为：1．
本题考查相似三角形的应用，熟知同一时刻物高与影长成正比是解题关键．
12、2.1
【解析】
试题分析：先要过D作出垂线段DE，根据角平分线的性质求出CD=DE，再根据已知即可求得D到AB的距离的大小．
解：过点D作DE⊥AB于E，
∵AD平分∠BAC，DE⊥AB，DC⊥AC
∴CD=DE
又BD：DC=2：1，BC=7.8cm
∴DC=7.8÷（2+1）=7.8÷3=2.1cm．
∴DE=DC=2.1cm．
故填2.1．
点评：此题主要考查角平分线的性质；根据角平分线上的点到角的两边的距离相等进行解答，各角线段的比求出线段长是经常使用的方法，比较重要，要注意掌握．
13、−.
【解析】
把交点坐标代入2个函数后，得到2个方程，求得a，b的解，整理求得的值即可．
【详解】
∵函数与y=x−1的图象的交点坐标为(a,b)，
∴b= ，b=a−1，
∴=a−1，
a−a−2=0，
(a−2)(a+1)=0，
解得a=2或a=−1，
∴b=1或b=−2，
∴的值为−.
故答案为：−.
此题考查反比例函数与一次函数的交点问题，解题关键在于把交点坐标代入2个函数后，得到2个方程
三、解答题（本大题共5个小题，共48分）
14、（1）详见解析；（2）详见解析
【解析】
（1）根据平行四边形的性质可得AB＝CD， AB∥CD，得证∠BAE＝∠DCF，可以证明△ABE≌△DCF（ASA），从而得出AE＝CF；
（2）根据全等三角形的性质可得∠AEB＝∠CFD，根据等角的补角相等可得∠AEF＝∠CFE，然后证明AE∥CF，从而可得四边形AECF是平行四边形．
【详解】
（1）∵四边形ABCD是平行四边形，
∴AB＝CD，∠DAB＝∠BCD，AB∥CD，
∠ABE＝∠CDF．
∵∠DAE＝∠BCF，
∴∠BAE＝∠DCF．
在△ABE和△CDF中，
，
∴△ABE≌△DCF（ASA）．
∴AE＝CF．
（2）∵△ABE≌△DCF，
∴∠AEB＝∠CFD，
∴∠AEF＝∠CFE，
∴AE∥CF，
∵AE＝CF，
∴四边形AECF是平行四边形．
本题考查了平行四边形和全等三角形的问题，掌握平行四边形的性质以及判定定理、全等三角形的性质以及判定定理、等角的补角相等是解题的关键．
15、作图见解析.
【解析】
延长AB，以点C为圆心，大于点C到直线AB的距离的长为半径画弧，交AB的延长线于点M和点N，再作线段MN的垂直平分线CD即可．
【详解】
如图，延长AB，
以点C为圆心，大于点C到直线AB的距离的长为半径画弧，
交AB的延长线于点M和点N，
分别以M、N为圆心，以大于MN一半长为半径画弧，两弧交于一点，过点C以及这点作直线，交MN于点D，
则线段CD即为所求作的.
本题考查作图-基本作图，掌握作垂直平分线的基本步骤为解题关键．
16、 (1)每部型手机的销售利润为元，每部型手机的销售利润为元；(2)①；②手机店购进部型手机和部型手机的销售利润最大；(3)手机店购进部型手机和部型手机的销售利润最大.
【解析】
（1）设每部型手机的销售利润为元，每部型手机的销售利润为元，根据题意列出方程组求解即可；
（2）①根据总利润=销售A型手机的利润+销售B型手机的利润即可列出函数关系式；
②根据题意，得，解得，根据一次函数的增减性可得当当时，取最大值；
（3）根据题意，，，然后分①当时，②当时，③当时，三种情况进行讨论求解即可.
【详解】
解：(1)设每部型手机的销售利润为元，每部型手机的销售利润为元.
根据题意，得，
解得
答：每部型手机的销售利润为元，每部型手机的销售利润为元.
(2)①根据题意，得，即.
②根据题意，得，解得.
，，
随的增大而减小.
为正整数，
当时，取最大值，.
即手机店购进部型手机和部型手机的销售利润最大.
(3)根据题意，得.
即，.
①当时，随的增大而减小，
当时，取最大值，即手机店购进部型手机和部型手机的销售利润最大；
②当时，，，即手机店购进型手机的数量为满足的整数时，获得利润相同；
③当时，，随的增大而增大，
当时，取得最大值，即手机店购进部型手机和部型手机的销售利润最大.
本题主要考查一次函数的应用，二元一次方程组的应用，解此题的关键在于熟练掌握一次函数的增减性.
17、x+y，．
【解析】
试题分析：根据分式的减法和除法可以化简题目中的式子，然后将x、y的值代入即可解答本题．
试题解析：原式= ==x+y，
当x=，y==2时，原式=﹣2+2=．
18、 (1)证明见解析；(2)AD=12.
【解析】
（1）根据平行四边的判定与性质，可得答案；
（2）根据AAS证明△AGF≌△BGE，再根据全等三角形的性质与平行四边形的性质即可求解．
【详解】
(1)证明：∵四边形是平行四边形，
∴，
∵，
∴四边形是平行四边形，
∴；
(2)解：∵，
∴，
∵点是的中点，
∴，
在与中，
，
∴，
∴，
∵，
∴，
∵四边形是平行四边形，
∴.
本题考查了平行四边形的判定与性质，全等三角形的判定与性质，关键是证明△AGF≌△BGE．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、无解
【解析】
二元一次方程组的解，就是两个函数图象的交点坐标，当两函数图象平行时，两个函数无交点，因此解析式所组成的方程组无解．
【详解】
∵直线y=-5x+2与y=-5x-3互相平行，
∴方程组无解，
故答案为：无解．
此题主要考查了一次函数与二元一次方程组的关系，关键是掌握二元一次方程组的解，就是两个函数图象的交点．
20、11cm1
【解析】
利用菱形的面积公式可求解．
【详解】
解：因为菱形的对角线互相垂直平分，
∵AC＝cm，BD＝cm，
则菱形ABCD的面积是cm1．
故答案为11cm1．
此题主要考查菱形的面积计算，关键是掌握菱形的面积计算方法．
21、．
【解析】
根据反比例函数的k确定图象在哪两个象限，再根据（x1，y1），（x2，y2），其中，确定这两个点均在第一象限，根据在第一象限内y随x的增大而减小的性质做出判断．
【详解】
解：反比例函数y＝图象在一、三象限，
（x1，y1），（x2，y2）在反比例函数y＝图象上，且，
因此（x1，y1），（x2，y2）在第一象限，
∵反比例函数y＝在第一象限y随x的增大而减小，
∴，
故答案为：．
本题考查了反比例函数的增减性，熟悉反比例函数的图象与性质是解题的关键．
22、5+或5-．
【解析】
分两种情况讨论：①当正方形ACFE边EF在AC左侧时，②当正方形ACFE边EF在AC右侧时．
【详解】
解：∵四边形ABCD是菱形，∠B=60°，
∴△ACD是等边三角形，且DO⊥AC．
∵菱形的边长为5，
∴DO= =
分两种情况讨论：
①当正方形ACFE边EF在AC左侧时，
过D点作DH2⊥EF，DH2长度表示点D到EF的距离，
DH2=5+DO=5+；
②当正方形ACFE边EF在AC右侧时，
过D点作DH1⊥EF，DH1长度表示点D到EF的距离，
DH1=5-DO=5-．
故答案为：5+或5-．
本题考查菱形的性质、正方形的性质、等边三角形的判定和性质，同时考查了分类讨论思想．解决此类问题要借助画图分析求解．
23、或
【解析】
分式方程去分母转化为整式方程，由分式方程有增根，得到最简公分母为0求出的值，代入整式方程求出的值即可．
【详解】
解：
去分母得：，
整理得：
由分式方程有增根，得到，
解得：或，
把代入整式方程得：；
把代入整式方程得：，
则的值为或．
故答案为：或
此题考查了分式方程的增根，增根确定后可按如下步骤进行：①化分式方程为整式方程；②把增根代入整式方程即可求得相关字母的值．
二、解答题（本大题共3个小题，共30分）
24、（1） ;（2）2400元.
【解析】
（1）根据题意可得A种塑料袋每天获利（2.4-2）x，B种塑料袋每天获利（3.6-3）（5000-x），共获利y元，列出y与x的函数关系式：y=（2.4-2）x+（3.6-3）（5000-x）．
（2）根据题意得2x+3（4500-x）≤10000，解出x的范围．得出y随x增大而减小．
【详解】
（1）由题意得：=
（2）由题意得：≤12000
解得：≥3000
在函数中，＜0
∴随的增大而减小
∴当=3000时，每天可获利最多，最大利润=2400
∴该厂每天最多获利2400元.
此题主要考查了一次函数的应用以及不等式组解法，解决问题的关键是读懂题意，找到关键描述语，找到所求的量的等量关系.
25、证明：（1）见解析
（2）见解析
【解析】
（1）根据AC⊥BC，BD⊥AD，得出△ABC与△BAD是直角三角形，再由AC=BD，AB=BA，根据HL得出△ABC≌△BAD，即可证出BC=AD．
（2）根据△ABC≌△BAD，得出∠CAB=∠DBA，从而证出OA=OB，△OAB是等腰三角形．
【详解】
证明：（1）∵AC⊥BC，BD⊥AD，∴△ABC与△BAD是直角三角形，
在△ABC和△BAD中，∵ AC="BD" ，AB=BA，∠ACB=∠BDA =90°，
∴△ABC≌△BAD（HL）．∴BC=AD．
（2）∵△ABC≌△BAD，∴∠CAB=∠DBA，∴OA=OB．
∴△OAB是等腰三角形．
26、（1）y=﹣，y=﹣x+2；（2）3；（1）-1＜x＜0或x＞1
【解析】
【分析】（1）欲求这两个函数的解析式，关键求k值．根据反比例函数性质，k绝对值为1且为负数，由此即可求出k；
（2）由函数的解析式组成方程组，解之求得A、C的坐标，然后根据S△AOC=S△ODA+S△ODC即可求出；
（1）根据图象即可求得．
【详解】解：（1）设A点坐标为（x，y），且x＜0，y＞0，
则S△ABO=•|BO|•|BA|=•（﹣x）•y=，
∴xy=﹣1，
又∵y=，
即xy=k，
∴k=﹣1．
∴所求的两个函数的解析式分别为y=﹣，y=﹣x+2；
（2）由y=﹣x+2，
令x=0，得y=2．
∴直线y=﹣x+2与y轴的交点D的坐标为（0，2），
∵A、C在反比例函数的图象上，
∴，
解得 ，，
∴交点A（﹣1，1），C为（1，﹣1），
∴S△AOC=S△ODA+S△ODC=OD•（|x1|+|x2|）=×2×（1+1）=3．
（1）-1＜x＜0或x＞1 .
【点睛】此题首先利用待定系数法确定函数解析式，然后利用解方程组来确定图象的交点坐标，及利用坐标求出线段和图形的面积．也考查了函数和不等式的关系．
题号
一
二
三
四
五
总分
得分
成本（元/个）
售价 （元/个）
2
2.4
3
3.6