初中数学苏科版（2024）八年级上册3.3 勾股定理的简单应用一等奖课件ppt

这是一份初中数学苏科版（2024）八年级上册3.3 勾股定理的简单应用一等奖课件ppt，共16页。PPT课件主要包含了特别提醒等内容，欢迎下载使用。

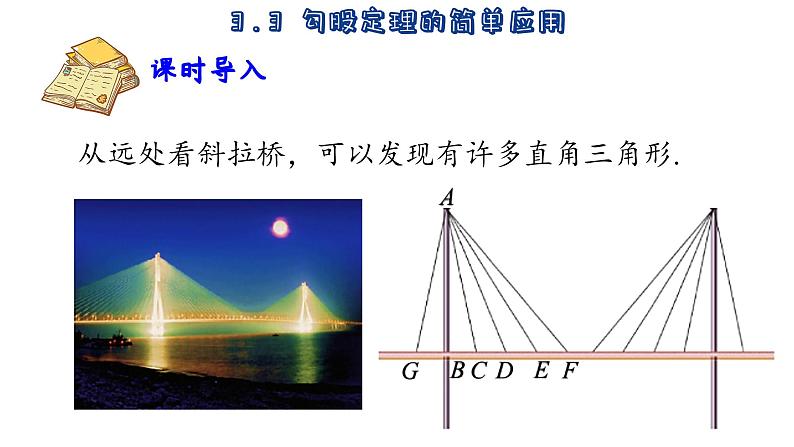
从远处看斜拉桥，可以发现有许多直角三角形.
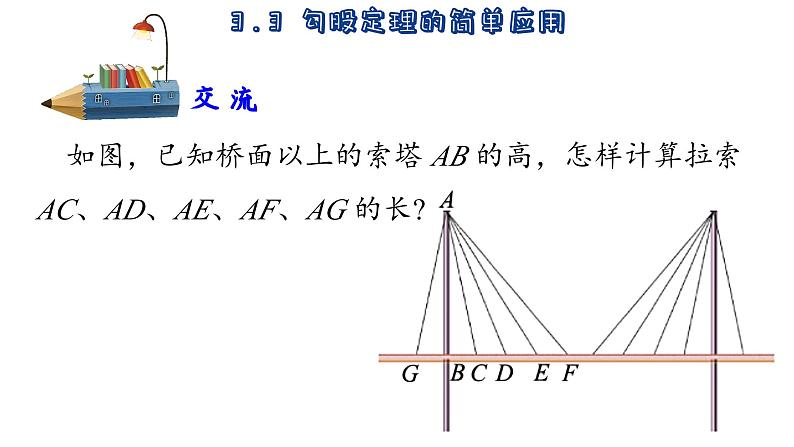
如图，已知桥面以上的索塔 AB 的高，怎样计算拉索 AC、AD、AE、AF、AG 的长?
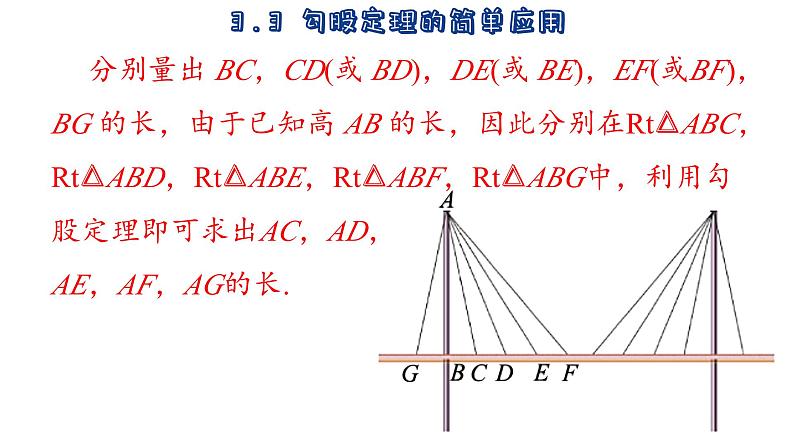
分别量出 BC，CD(或 BD)，DE(或 BE)，EF(或BF)，BG 的长，由于已知高 AB 的长，因此分别在Rt△ABC，Rt△ABD，Rt△ABE，Rt△ABF，Rt△ABG中，利用勾股定理即可求出AC，AD，AE，AF，AG的长.
常见的应用主要有以下几个类型：
(1) 已知直角三角形的两边求第三边；(2) 已知直角三角形的一边，确定另外两边的关系；(3) 证明含有平方关系的几何问题；(4) 对于一些非直角三角形的实际问题，首先要建立直角三角形模型，然后利用勾股定理构建方程或方程组解决.
运用勾股定理解决实际问题的一般步骤：1. 从实际问题中抽象出几何图形；2. 确定要求的线段所在的直角三角形；3. 找准直角边和斜边，根据勾股定理建立等量关系；4. 求得结果.
例 1 《九章算术》中有一道“折竹”问题：“今有竹高一丈，末折抵地，去根三尺，问折者高几何?”题意是：一根竹子原高 1丈(1 丈＝10尺)，中部有一处折断，竹档触地面处离竹根 3 尺，试问折断处离地面多高?
解：如图，竹子在点 A 处折断，竹梢点 B 着地，△ABC 是直角三角形. 设AC＝x尺，则AB＝(10－x)尺由勾股定理，得 x2＋32＝ (10－x)2. 解得 x＝4.55. ∴折断处离地面 4.55 尺.
一架长 5 m 的梯子，斜靠在一竖直墙上，这时梯足距墙脚 3 m，若梯子的顶端下滑1 m，则梯足将滑动 ( ) A. 0 m B. 1 m C. 2 m D. 3 m
例2 如图，AD 是△ABC 的中线，AD＝24，AB＝26，BC ＝ 20. 求 AC .
如图， 在△ABC 中，D 是AB 边的中点，DE⊥AB 于点D， 交AC 于点E， 且 AE2 －CE2＝BC2. (1) 试说明：∠C＝90°； (2) 若DE＝6，BD＝8，求CE 的长．
解：如图所示，连接BE， ∵ D 是AB 边的中点，DE⊥AB 于点D， ∴ DE 垂直平分AB， ∴ AE＝BE．又∵ AE2 － CE2＝BC2， ∴ BE2 － CE2＝BC2，即BE2＝BC2＋CE2． ∴△ BCE 是直角三角形，且∠C＝90°；
(1) 试说明：∠C＝90°；
解：在Rt△BDE 中，∠BDE＝90°， DE＝6，BD＝8，由勾股定理，得62＋82＝BE2．则BE＝10， ∴ AE=10．设 CE＝x，则AC＝10＋x，而AB＝2BD＝16．
(2) 若DE＝6，BD＝8，求CE 的长．
在Rt△ABC 中，BC2＝AB2 － AC2 ＝162 －(10＋x)2，在Rt△BCE 中，BC2＝EB2－EC2 ＝102－x2．∴ 162 －(10＋x)2＝102 － x2．解得x＝2.8， ∴ CE＝2.8．