初中第六章 几何图形初步6.1 几何图形第1课时教案设计

这是一份初中第六章 几何图形初步6.1 几何图形第1课时教案设计，共5页。教案主要包含了情境引入，教学建议，对应训练，课堂总结，知识结构，作业布置等内容，欢迎下载使用。
6.1.1 立体图形与平面图形
第1课时 认识几何图形




解题大招 几何图形的认识
1.立体图形的基本特征
2.几何图形的分类
例1 下列立体图形中，表面只包含平面图形的是（ D ）


例2 如图所示为八个立体图形.

其中，是柱体的序号为①②⑤⑦⑧ ，是锥体的序号为④⑥ ，是球的序号为③ .

培优点 七巧板中的图形组合及其面积问题
（数学文化·七巧板） “七巧板”是我国古代人民创造的益智游戏，被西方人称为“东方魔板”，如图所示是用同一副七巧板拼出的几何图形.
（1）你能在图②中找出你熟悉的几何图形吗？
（2）刘伟用七巧板重新组合拼成了一个图形（如图③），已知图①中大正方形的边长为8 cm，请你计算图③中阴影部分的面积.
（3）你自己能设计出由七巧板拼出的图案吗？请你画出你设计的图案.
分析：（1）七巧板是由5个大小不一的等腰直角三角形、1个平行四边形、1个正方形构成.无论其怎么组合，都是这几个图形；
（2）可根据下表中的面积关系计算：
（3）根据自己喜好拼接即可.
解：（1）直角三角形、正方形、平行四边形.
（2）因为图①中大正方形的边长为8 cm，所以大正方形的面积是64 cm2，由图③的拼法可知，阴影部分的面积占大正方形面积的 ，所以图③中阴影部分的面积是 （cm2）.
（3）能，如图所示.（拼法不唯一）教学目标
课题
6.1.1 第1课时 认识几何图形
授课人
素养目标
1.了解从实物抽象出来的几何图形等概念.
2.认识圆柱、圆锥、棱柱、棱锥、球，并能用语言描述它们的某些特征及能对它们进行简单的分类.
3.通过平面图形的学习，巩固有关图形知识，进一步建立空间观念.学会运用观察法、分类法，培养学生观察、分析的能力及合作交流的能力.
教学重点
在具体的情境中认识圆柱、圆锥、棱柱、棱锥、球，并能用语言描述它们的某些特征及能对它们进行简单的分类.
教学难点
知道柱体与锥体；从具体事物中抽象出几何图形.
教学活动
教学步骤
师生活动
活动一：创设情境，导入新课
【情境引入】
欣赏下面这些图片，我们现实生活中的图形世界多姿多彩.各种各样的物体都有颜色、质量、材质、形状、大小、位置关系等方面的特征，其中形状、大小和位置关系是几何中要研究的内容.让我们一起走进本课时的学习吧！
【教学建议】
教学中可根据当地实际，选择其他一些图形进行教学，也可以利用信息技术工具多呈现一些图形，让学生体会几何图形的丰富多彩.
设计意图
通过呈现生活中的一些建筑、物体和一些艺术图案，让学生能从中发现熟悉的几何图形，感受几何图形与我们的生活息息相关.
活动二：合作交流，新知探究
探究点1 立体图形
问题1 画一画下面这些小学学过的图形，结合“活动一”中的实物图，想一想它们是怎么得出的？
它们都是从形形色色的物体外形中得出的.
问题2 上面这些小学学过的图形都是几何图形.观察上面诸如长方体、圆柱、圆锥、球等几何图形，与三角形、四边形、圆等几何图形相比，它们有什么共同特征区别于其他几何图形呢？
这些几何图形的各部分不都在同一平面内，它们是立体图形.
【教学建议】
对于问题1，2，教学时不要求学生对几何图形进行严格定义，学生只要能对给出的几何图形进行识别，或能从实际物体中“发现”它们即可.教学时重点是要让学生意识到所有的几何图形都是从现实生活中抽象出来的，并且知道立体图形最显著的特征是什么.
设计意图
先由熟悉的物体引出立体图形的概念，再结合包装盒、储物盒、金字塔等实物例子，说明从实物可以得到立体图形的形象，再安排一些实物与立体图形的对应，
教学步骤
师生活动
都意在说明抽象的过程，另一方面也说明学习几何图形知识广泛的实际应用价值.
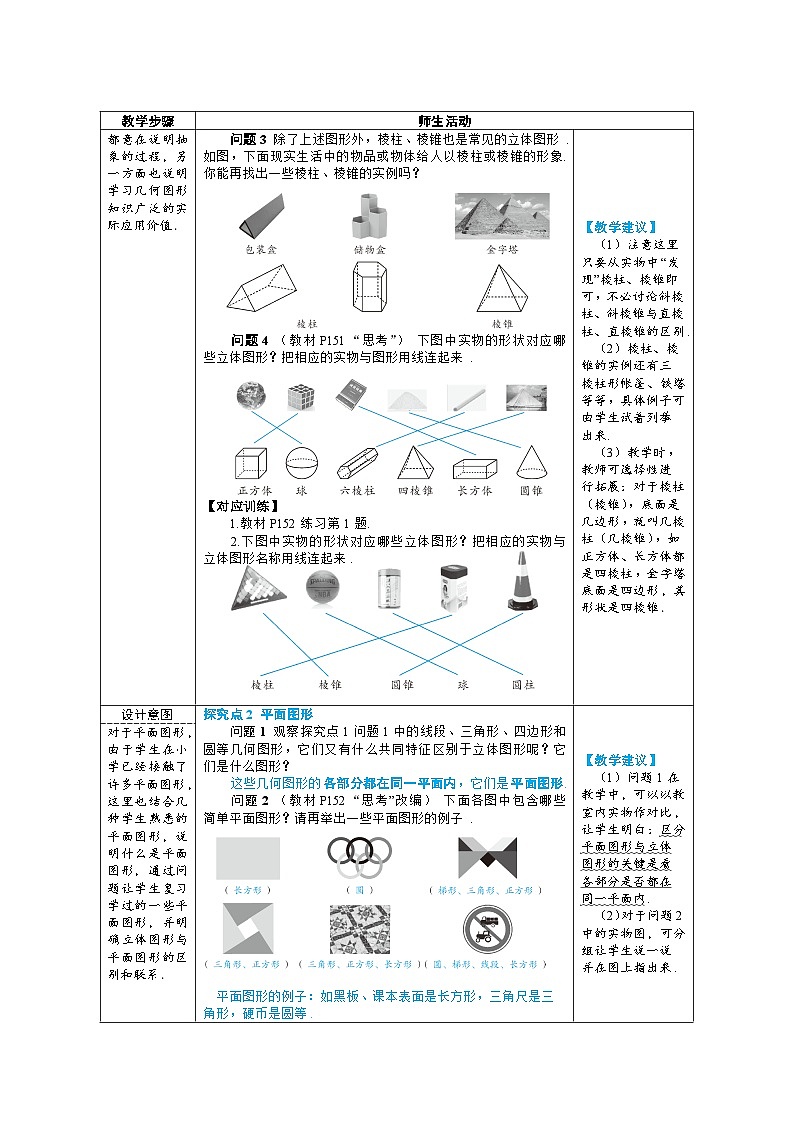
问题3 除了上述图形外，棱柱、棱锥也是常见的立体图形.如图，下面现实生活中的物品或物体给人以棱柱或棱锥的形象.你能再找出一些棱柱、棱锥的实例吗？
问题4 （教材P151“思考”） 下图中实物的形状对应哪些立体图形？把相应的实物与图形用线连起来.
【对应训练】
1.教材P152练习第1题.
2.下图中实物的形状对应哪些立体图形？把相应的实物与立体图形名称用线连起来.
【教学建议】
（1）注意这里只要从实物中“发现”棱柱、棱锥即可，不必讨论斜棱柱、斜棱锥与直棱柱、直棱锥的区别.
（2）棱柱、棱锥的实例还有三棱柱形帐篷、铁塔等等，具体例子可由学生试着列举出来.
（3）教学时，教师可选择性进行拓展：对于棱柱（棱锥），底面是几边形，就叫几棱柱（几棱锥），如正方体、长方体都是四棱柱，金字塔底面是四边形，其形状是四棱锥.
设计意图
探究点2 平面图形
问题1 观察探究点1问题1中的线段、三角形、四边形和圆等几何图形，它们又有什么共同特征区别于立体图形呢？它们是什么图形？
这些几何图形的各部分都在同一平面内，它们是平面图形.
问题2 （教材P152“思考”改编） 下面各图中包含哪些简单平面图形？请再举出一些平面图形的例子.
平面图形的例子：如黑板、课本表面是长方形，三角尺是三角形，硬币是圆等.
【教学建议】
（1）问题1在教学中，可以以教室内实物作对比，让学生明白：区分平面图形与立体图形的关键是看各部分是否都在同一平面内.
（2）对于问题2中的实物图，可分组让学生说一说并在图上指出来.
对于平面图形，由于学生在小学已经接触了许多平面图形，这里也结合几种学生熟悉的平面图形，说明什么是平面图形，通过问题让学生复习学过的一些平面图形，并明确立体图形与平面图形的区别和联系.
教学步骤
师生活动
问题3 结合下面两组图形，你认为平面图形与立体图形有什么关联？
从上面图形可以看出，很多立体图形中的某些部分是平面图形.

【对应训练】
1.下面四个几何图形中，是平面图形的是（ D ）

2.观察下面两个图案.
（1）这两个图案中包含哪些简单平面图形？
（2）图①中包含几个四边形？图②中包含几个三角形？
解：（1）图①包含三角形、正方形、长方形、梯形；图②包括三角形、正方形、平行四边形.
（2）图①中包含四个四边形，图②中包含五个三角形.
（3）问题3仍可以拿实物进行举例说明，要让学生能指出来.
活动三：典例精析，巩固提升
例 （教材P152练习第2题） 图中的各立体图形的表面中包含哪些平面图形？指出这些平面图形在立体图形中的位置.
解：从左往右第一个图中上、下底面是圆；第二个图中底面是圆；第三个图中上、下底面是五边形，侧面是五个长方形；第四个图中底面是六边形，侧面是六个三角形；第五个图中底面和与其相邻的侧面是五个长方形，上面是四个三角形.
【对应训练】
如图，说出各立体图形的名称，它们的表面中包含哪些平面图形？指出这些平面图形在立体图形中的位置.
解：第①个图形是三棱锥，表面都是三角形，它在三棱锥的四个面上.
第②个图形是三棱柱，表面包含三角形、长方形，三角形位于三棱柱的上、下底面，长方形位于三棱柱的三个侧面.
第③个图形是四棱柱，表面包含梯形、长方形，梯形位于四棱柱的上、下底面，长方形位于四棱柱的四个侧面.
第④个图形是一个组合图形，上面是一个圆锥，下面是一个圆柱，表面包含圆、圆环，圆位于下底面，圆环部分位于其中圆柱的上底面.
【教学建议】
（1）教师可以先讲第一个图形，给学生做一个示范，引导学生思考和回答，后面的几个图形可以让学生小组讨论之后，由代表发言.
（2）①注意例题最后一个组合图形的上面是四个三角形.
②【对应训练】中注意有的学生可能把最后一个图中圆锥、圆柱的侧面理解成扇形或长方形，如有这种情况要纠正.
设计意图
在学生明确了立体图形和平面图形的概念的基础上，培养学生的识别能力，并建立概念之间的联系.
教学步骤
师生活动
活动四：随堂训练，课堂总结
【课堂总结】师生一起回顾本节课所学主要内容，并请学生回答以下问题：
1.几何研究哪些内容？什么是几何图形？
2.什么是立体图形？
3.什么是平面图形？平面图形和立体图形的区别与联系是什么？
【知识结构】
【作业布置】
1.教材P157习题6.1第1题.
板书设计
教学反思
在本节课的教学设计中，改变以往注重知识的传授的倾向，强调学生形成积极主动的学习态度，关注学生的学习兴趣和体验.应用多媒体给学生展示生动的图片，引导学生观察生活中的美妙画面，激发学生的学习兴趣.在学习中注重让学生主动参与学习活动，观察感受，通过自主、合作、探究学习，激发学生的联想与再创造能力.