数学八年级上册2.2 等腰三角形达标测试

这是一份数学八年级上册2.2 等腰三角形达标测试，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
班级： 姓名：
一、选择题
1．如图，AB∥CD，点E在线段BC上，BA=BE，若∠C=32°，则∠A的度数（ ）
A．72°B．74°C．76°D．78°
2．已知△ABC的三边长分别为2、2、3，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画（ ）条．
A．3B．4C．5D．6
3．如图，在△ABC中，∠ACB=90°，以AC为底边在△ABC外作等腰△ACD，过点D作∠ADC的平分线分别交AB，AC于点E，F．若BC=5，∠CAB=30°，点P是直线DE上的一个动点，则△PBC周长的最小值为（ ）
A．15B．17C．18D．20
4．如图，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为点D，交AC于点E，∠A=∠ABE，若AC=10，BC=6，则BD的长为（ ）
A．5B．3C．4D．2
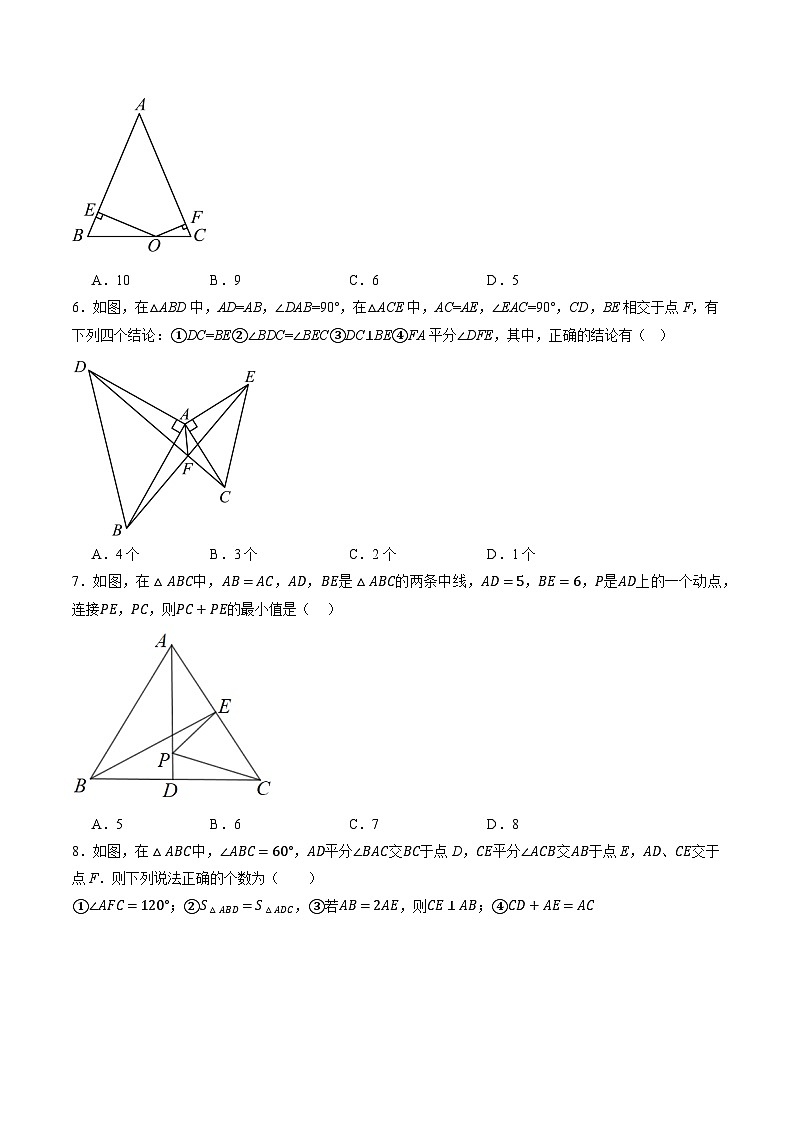
5．如图，△ABC是等腰三角形，AB=AC=6，点O是底边BC上任意一点，OE⊥AB于点E，OF⊥AC于点F，若该等腰三角形的面积为15，则OE+OF的值为（ ）

A．10B．9C．6D．5
6．如图，在△ABD中，AD=AB，∠DAB=90°，在△ACE中，AC=AE，∠EAC=90°，CD，BE相交于点F，有下列四个结论：①DC=BE②∠BDC=∠BEC③DC⊥BE④FA平分∠DFE，其中，正确的结论有（ ）
A．4个B．3个C．2个D．1个
7．如图，在△ABC中，AB=AC，AD，BE是△ABC的两条中线，AD=5，BE=6，P是AD上的一个动点，连接PE，PC，则PC+PE的最小值是（ ）
A．5B．6C．7D．8
8．如图，在△ABC中，∠ABC=60°，AD平分∠BAC交BC于点D，CE平分∠ACB交AB于点E，AD、CE交于点F．则下列说法正确的个数为（ ）
①∠AFC=120°；②S△ABD=S△ADC，③若AB=2AE，则CE⊥AB；④CD+AE=AC
A．1个B．2个C．3个D．4个
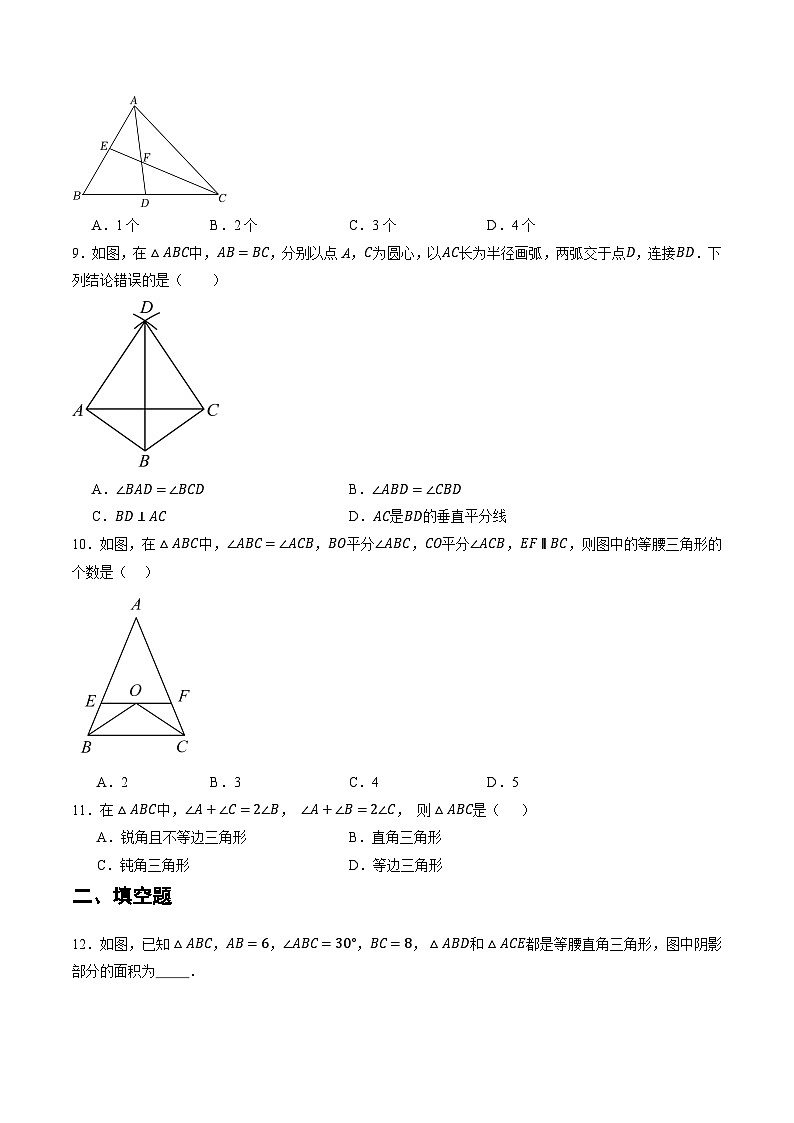
9．如图，在△ABC中，AB=BC，分别以点A，C为圆心，以AC长为半径画弧，两弧交于点D，连接BD．下列结论错误的是（ ）
A．∠BAD=∠BCDB．∠ABD=∠CBD
C．BD⊥ACD．AC是BD的垂直平分线
10．如图，在△ABC中，∠ABC=∠ACB，BO平分∠ABC，CO平分∠ACB，EF∥BC，则图中的等腰三角形的个数是（ ）
A．2B．3C．4D．5
11．在△ABC中，∠A+∠C=2∠B， ∠A+∠B=2∠C， 则△ABC是（ ）
A．锐角且不等边三角形B．直角三角形
C．钝角三角形D．等边三角形
二、填空题
12．如图，已知△ABC，AB=6，∠ABC=30°，BC=8，△ABD和△ACE都是等腰直角三角形，图中阴影部分的面积为 ．
13．如图， 在△ABC中，BD平分∠ABC，DE∥BC，AD=4，△AED的周长为11，那么AB的长是 ．

14．如图，等边△ABC中，点D、E分别在边AB、BC上，把△BDE沿直线DE翻折，使点B落在点B′处，DB′、EB′分别交边AC于点F、G．如果测得∠GEC=36°，那么∠ADF= ．
15．若等腰三角形ABC一个外角是100度，那么它的底角是 度．
16．如图，△ABC和△ECD都是等腰直角三角形，∠BCA=∠DCE=90°，△ABC的顶点A在△ECD的斜边DE上．下列结论：①△ACE≌△BCD；②∠DAB=∠ACE；③AE+AC=CD；④△ABD是直角三角形．其中正确的是 （填写序号）．
三、解答题
17．如图，AD是△ABC的角平分线，DE⊥AC，垂足为E,BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF．
(1)求证：△CDE≌△BDF；
(2)若△ABC的面积是18，DF=3，求AB长．
18．如图，△ABC是等腰三角形，AB=AC，用尺规作图法在BC上作一点D，使得AD将△ABC分成两个全等的三角形．（保留作图痕迹，不写作法）
19．如图，已知直线l和l外一点A，请用尺规作图法，求作一个等腰直角△ABC，使得顶点B和顶点C都在直线l上．（作出符合题意的一个等腰直角三角形即可，保留作图痕迹，不写作法）
20．如图，已知在ΔABC中，AB=AC，点D、E在边BC上，且AD=AE．试说明BD=CE的理由．
21．如图，在△ABC中，∠ACB的平分线CD交AB于点E，点F是AC上一点，连接BD、EF．
(1)若AC=BC，∠D=35°，求∠ABD的度数；
(2)若∠D=∠BCD，∠AFE+∠CBD=180°，判断EF与BC的位置关系，并说明理由．
22．（1）如图1，已知：在△ABC中，AB=AC=10，BD平分∠ABC，CD平分∠ACB，过点D作EF∥BC，分别交AB、AC于E、F两点，则图中共有 个等腰三角形；EF与BE、CF之间的数量关系是 ，△AEF的周长是
（2）如图2，若将（1）中“△ABC中，AB=AC=10”改为“若△ABC为不等边三角形，AB=8，AC=10”其余条件不变，则图中共有 个等腰三角形；EF与BE、CF之间的数量关系是什么？证明你的结论，并求出△AEF的周长
（3）已知：如图3，D在△ABC外，AB>AC，且BD平分∠ABC，CD平分ΔABC的外角∠ACG，过点D作DE∥BC，分别交AB、AC于E、F两点，则EF与BE、CF之间又有何数量关系呢？直接写出结论不证明．
等腰三角形的性质与判定专项训练
参考答案
1．如图，AB∥CD，点E在线段BC上，BA=BE，若∠C=32°，则∠A的度数（ ）
A．72°B．74°C．76°D．78°
【答案】B
【详解】解：∵ AB∥CD，∠C=32°，
∴ ∠B=∠C=32°，
∵ BA=BE，
∴ ∠A=∠AEB=180°−∠B2=74°，
故选：B．
2．已知△ABC的三边长分别为2、2、3，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画（ ）条．
A．3B．4C．5D．6
【答案】B
【详解】解：设AB=AC=2，BC=3，
∵BC>AB，
∴有以下四种情况，
①以点B为圆心，以AB为半径画弧交BC于D，作直线AD，如图1所示：

则AB=BD=2，
∴直线AD将△ABC分割成两个三角形，其中的一个是等腰三角形；
②以点C为圆心，以AC为半径画弧交BC于E，作直线AE，如图2所示：

则AC=CE=2，
∴直线AE将△ABC分割成两个三角形，其中的一个是等腰三角形；
③作线段AB的垂直平分线交BC于点F，作直线AF，如图3所示：

则AF=BF，
∴直线AF将△ABC分割成两个三角形，其中的一个是等腰三角形；
④作线段AC的垂直平分线交BC于点H，作直线AH，如图4所示：

则AH=HF，
∴直线AH将△ABC分割成两个三角形，其中的一个是等腰三角形．
综上所述：这样的直线最多可以画4条，
故选：B．
3．如图，在△ABC中，∠ACB=90°，以AC为底边在△ABC外作等腰△ACD，过点D作∠ADC的平分线分别交AB，AC于点E，F．若BC=5，∠CAB=30°，点P是直线DE上的一个动点，则△PBC周长的最小值为（ ）
A．15B．17C．18D．20
【答案】A
【详解】解：∵△ACD是以AC为底边的等腰三角形，DE平分∠ADC，
∴DE垂直平分AC，
∴点A与点C关于DE对称，
∴PC=PA，
如图所示，当点P与点E重合时，PC+PB=PA+PB=AB，
此时△PBC的周长最小，
∵BC=5，∠ACB=90°，∠CAB=30°，
∴AB=2BC=10，
∴△PBC周长的最小值为：PB+PC+BC=PB+PA+BC=AB+BC=10+5=15，
故选：A．
4．如图，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为点D，交AC于点E，∠A=∠ABE，若AC=10，BC=6，则BD的长为（ ）
A．5B．3C．4D．2
【答案】D
【详解】∵CD平分∠ACB，
∴∠BCD=∠ECD，
∵BE⊥CD，
∴∠BDC=∠EDC=90°，
在△BCD和△ECD中，
∠BCD=∠ECDCD=CD∠BDC=∠EDC，
∴△BCD≌△ECDSAS，
∴DB=DE，BC=EC，
∵∠A=∠ABE，
∴AE=BE，
∵AC=10，BC=6，
∴EC=6，AE+EC=10，
∴AE=4，
∵BE=ED+DB=2DB=4，
∴DB=2．
故选：D．
5．如图，△ABC是等腰三角形，AB=AC=6，点O是底边BC上任意一点，OE⊥AB于点E，OF⊥AC于点F，若该等腰三角形的面积为15，则OE+OF的值为（ ）

A．10B．9C．6D．5
【答案】D
【详解】解：连接AO，

由题可知：S△AOC=12×AC×OF，
S△AOB=12×AB×OE，
∵S△AOC+S△AOB=S△ABC，
∴12×AC×OF+12×AB×OE=15，
∵AB=AC，
∴12×AB×OE+OF=15，
∵BA=6，
∴OE+OF=5，
故选D．
6．如图，在△ABD中，AD=AB，∠DAB=90°，在△ACE中，AC=AE，∠EAC=90°，CD，BE相交于点F，有下列四个结论：①DC=BE②∠BDC=∠BEC③DC⊥BE④FA平分∠DFE，其中，正确的结论有（ ）
A．4个B．3个C．2个D．1个
【答案】B
【详解】∵∠DAB=∠EAC=90°
∴∠DAB+∠BAC=∠EAC+∠BAC
∴在△DAC和△BAE中
AD=AB∠DAC=∠BAEAE=AC
∴△DAC≅△BAE
∴DC=BE，①正确
∠ADF=∠ABE
∵AB，AE不确定相等
∴∠ABE和∠AEB不确定相等
∵△ABD和△ACE是等腰直角三角形
∴∠ADB=∠AEC=45°
∵∠BDC=45°−∠ADC，∠BEC=45°−∠AEB
∴∠BDC和∠BEC不确定相等，②错误
∵∠ADF=∠ABE，∠AOD=∠BOF，∠DAB=90°
∴∠ADF+∠AOD=90°
∴∠ABE+∠BOF=90°
∴DC⊥BE，③正确
过点AM⊥DC于点M，AN⊥BE于点N
∵△DAC≅△BAE
∴AM=AN
∴AF平分∠DFE，④正确
∴①③④正确
故选：B．
7．如图，在△ABC中，AB=AC，AD，BE是△ABC的两条中线，AD=5，BE=6，P是AD上的一个动点，连接PE，PC，则PC+PE的最小值是（ ）
A．5B．6C．7D．8
【答案】B
【详解】解：如下图，连接PB，
∵AB=AC，BD=CD，
∴AD⊥BC，
∴PB=PC，
∴PC+PE=PB+PE，
∵PE+PB≥BE，
∴P、B、E共线时，PB+PE的值最小，最小值为BE的长度，
∵BE=6，
∴CP+EP的最小值是6，
故选：B．
8．如图，在△ABC中，∠ABC=60°，AD平分∠BAC交BC于点D，CE平分∠ACB交AB于点E，AD、CE交于点F．则下列说法正确的个数为（ ）
①∠AFC=120°；②S△ABD=S△ADC，③若AB=2AE，则CE⊥AB；④CD+AE=AC
A．1个B．2个C．3个D．4个
【答案】C
【详解】∵∠ABC=60°，
∴∠BAC+∠BCA=120°，
∴12∠BAC+∠BCA=60°，
∵AD平分∠BAC交BC于点D，CE平分∠ACB交AB于点E，
∴∠AFC=180°−12∠BAC+∠BCA=120°，
故①正确；
若S△ABD=S△ADC，
∴BD=DC,无法确定，
故②错误；
∵ AB=2AE，
∴BE=AE，
过点EG⊥AC,EH⊥BC，垂足分别为G，H，
∵CE平分∠ACB，
∴EG=EH；
∴△ECH≌△ECGHL,
∴CH=CG；
∴△BEH≌△AEGHL,
∴BH=AG；
∴AC=BC，
∴CE⊥AB，
故③正确；
作CG平分∠AFC交AC于点G，∵∠AFC=120°，
∴∠AFE=∠AFG=∠DFC=∠GFC=60°，
∵∠EAF=∠GAF,AF=AF,∠DCF=∠GCF,CF=CF
∴△DFC≌△GFCASA，△AFE≌△AFGASA∴AE=AG,CD=CG，
∵AC=AG+CG，
∴CD+AE=AC，
∴④正确．
故选C．
9．如图，在△ABC中，AB=BC，分别以点A，C为圆心，以AC长为半径画弧，两弧交于点D，连接BD．下列结论错误的是（ ）
A．∠BAD=∠BCDB．∠ABD=∠CBD
C．BD⊥ACD．AC是BD的垂直平分线
【答案】D
【详解】解：∵BA=BC，则∠BAC=∠BCA
∵DA=CD，则∠DAC=∠DCA
∴∠BAD=∠BCD，故A结论正确；
根据作图方法可得AD=AC=CD，
∵BA=BC，
∴点B在AC的垂直平分线上，
∵AD=CD，
∴点D在AC的垂直平分线上，
∴BD是AC的垂直平分线，故C结论正确；D结论错误；
∵BD⊥AC，BA=BC
∴∠ABD=∠CBD，故B结论正确；
故选：D．
10．如图，在△ABC中，∠ABC=∠ACB，BO平分∠ABC，CO平分∠ACB，EF∥BC，则图中的等腰三角形的个数是（ ）
A．2B．3C．4D．5
【答案】D
【详解】解：∵ ∠ABC=∠ACB，
∴AB=AC，即△ABC为等腰三角形；
∵ BO平分∠ABC，
∴ ∠EBO=∠CBO=12∠ABC，
∵ EF∥BC，
∴ ∠EOB=∠CBO，∠AEF=∠ABC=∠ACB=∠AFE，
∴ ∠EBO=∠EOB，△AEF为等腰三角形；
∴ △EOB为等腰三角形；
∵ CO平分∠ACB，
∴ ∠FCO=∠BCO=12∠ACB，
同理可证，△FOC为等腰三角形；
∵ 12∠ABC=12∠ACB，
∴ ∠CBO=∠BCO，
∴ △BOC为等腰三角形；
综上所述，图中的等腰三角形的个数是5个，
故选：D．
11．在△ABC中，∠A+∠C=2∠B， ∠A+∠B=2∠C， 则△ABC是（ ）
A．锐角且不等边三角形B．直角三角形
C．钝角三角形D．等边三角形
【答案】D
【详解】解：∵∠A+∠C=2∠B，∠A+∠B+∠C=180°，
∴3∠B=180°，
∴∠B=60°；
∵∠A+∠B=2∠C，∠A+∠B+∠C=180°，
∴3∠C=180°，
∴∠C=60°，
∴∠A=180°−∠B−∠C=60°，
∴∠A=∠B=∠C=60°，
∴△ABC是等边三角形，
故选：D．
12．如图，已知△ABC，AB=6，∠ABC=30°，BC=8，△ABD和△ACE都是等腰直角三角形，图中阴影部分的面积为 ．
【答案】12
【详解】解：过A作AH⊥BC于H，
∴∠AHB=∠AHC=90°，
∵AB=6，∠ABC=30°，
∴AH=12AB=3，
延长HA交DE于P，
过E作EG⊥AP于G，过D作DF⊥AP于F，
∴∠F=∠AHB=∠BAD=90°，
∴∠BAH+∠DAF=∠DAF+∠ADF=90°，
∴∠BAH=∠ADF，
∵AD=AB，
∴△ADF≌△BAHAAS，
∴DF=AH，
同理，△ACH≌△EAG，
∴EG=AH，
∴DF=EG，
∵∠F=∠AGE=90°，∠DPF=∠EPG，
∴△PDF≌△PEGAAS，
∴图中阴影部分的面积=△ABC的面积=12BC⋅AH=12×8×3=12，
故答案为：12．
13．如图， 在△ABC中，BD平分∠ABC，DE∥BC，AD=4，△AED的周长为11，那么AB的长是 ．

【答案】7
【详解】解：∵BD平分∠ABC，
∴∠EBD=∠DBC，
∵DE∥BC，
∴∠EDB=∠DBC，
∴∠EBD=∠EDB，
∴EB=ED，
∵△AED的周长等于11，
∴AE+ED+AD=11，
∴AE+EB+AD=11，
∴AB+AD=11，
∵AD=4，
∴AB=7，
故答案为：7．
14．如图，等边△ABC中，点D、E分别在边AB、BC上，把△BDE沿直线DE翻折，使点B落在点B′处，DB′、EB′分别交边AC于点F、G．如果测得∠GEC=36°，那么∠ADF= ．
【答案】84°/84度
【详解】解：∵△ABC为等边三角形，
∴∠B=60°，
∵∠GEC=36°，
∴∠BEG=180°−∠GEC=180°−36°=144°，
由翻折的性质得：∠BED=∠GED，∠BDE=∠FDE，
∴∠BED= 12 ∠BEG= 12 ×144°=72°，
∴∠BDE=180°−∠B−∠BED=180°−60°−72°=48°，
∴∠BDE=∠FDE=48°，
∴∠BDF=∠BDE+∠FDE=96°，
∴∠ADF=180°−∠BDF=180°−96°=84°．
故答案为：84°．
15．若等腰三角形ABC一个外角是100度，那么它的底角是 度．
【答案】50或80
【详解】∵等腰三角形的一个外角是100°，
∴等腰三角形的一个内角是80°，
当80°为顶角时，其他两个角都是底角且等于50°，
当80°为底角时，其他两个角为80°、20°，
∴等腰三角形的底角为50°或80°．
故答案为：50或80．
16．如图，△ABC和△ECD都是等腰直角三角形，∠BCA=∠DCE=90°，△ABC的顶点A在△ECD的斜边DE上．下列结论：①△ACE≌△BCD；②∠DAB=∠ACE；③AE+AC=CD；④△ABD是直角三角形．其中正确的是 （填写序号）．
【答案】①②④
【详解】∵ △ABC与△ECD都是等腰直角三角形，
∴ CA=CB，∠CAB=∠CBA=45°，CD=CE，∠E=∠CDE=45°．
∵ ∠ACE+∠ACD=∠ACD+∠BCD，
∴ ∠ACE=∠BCD．
在△ACE与△BCD中，
CE=CD∠ACE=∠BCDCA=CB
∴ △ACE≌△BCDSAS，故①正确；
∵ ∠DAC=∠E+∠ACE，
∴ ∠DAB+∠BAC=∠E+∠ACE．
∵ ∠E=∠CDE=45°，
∴ ∠DAB=∠ACE，故②正确；
∵ AE+AC>CE，CE=CD，
∴ AE+AC>CD，故③错误；
∵ △ACE≌△BCD，
∴ ∠BDC=∠E=45°．
∵ ∠CDE=45°，
∴ ∠ADB=∠ADC+∠BDC=45°+45°=90°，故④正确．
故答案为：①②④
17．如图，AD是△ABC的角平分线，DE⊥AC，垂足为E,BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF．
(1)求证：△CDE≌△BDF；
(2)若△ABC的面积是18，DF=3，求AB长．
【详解】（1）解：∵BC平分∠ABF,
∴∠ABC=∠FBC，
∵BF∥AC,，
∴∠ACB=∠FBC
∴∠ABC=∠ACB,
∴AB=AC．
∵AD是△ABC角平分线，
∴DB=DC,AD⊥BC．
在△CDE和△BDF中，
∠C=∠DBFDC=DB∠CDE=∠BDF，
∴△CDE≌△BDFASA．
（2）解：过点D作DG⊥AB于点G，
∵△CDE≌△BDF，
∴DE=DF=3,CD=BD，
∵AD平分∠CAB,DE⊥AC,DG⊥AB，
∴DG=DE=3，
∵CD=BD，
∴S△ABD=12S△ABC=9，
即12AB⋅DG=9，
∴AB=6．
18．如图，△ABC是等腰三角形，AB=AC，用尺规作图法在BC上作一点D，使得AD将△ABC分成两个全等的三角形．（保留作图痕迹，不写作法）
【详解】解：如图所示，点D为所求，
∵ AB=AC,AD=AD,BD=CD，
∴ △ABD≌△ACDSSS．
19．如图，已知直线l和l外一点A，请用尺规作图法，求作一个等腰直角△ABC，使得顶点B和顶点C都在直线l上．（作出符合题意的一个等腰直角三角形即可，保留作图痕迹，不写作法）
【详解】解：等腰直角△ABC如图所示：
20．如图，已知在ΔABC中，AB=AC，点D、E在边BC上，且AD=AE．试说明BD=CE的理由．
【详解】过点A作AH⊥BC，垂足为点H，
∵AB=AC，AH⊥BC，
∴BH=CH，
∵AD=AE，AH⊥BC，
∴DH=EH，
∴BH−DH=CH−EH，
∴BD=CE．
21．如图，在△ABC中，∠ACB的平分线CD交AB于点E，点F是AC上一点，连接BD、EF．
(1)若AC=BC，∠D=35°，求∠ABD的度数；
(2)若∠D=∠BCD，∠AFE+∠CBD=180°，判断EF与BC的位置关系，并说明理由．
【详解】（1）解：∵AC=BC，CE平分∠ACB，
∴CD⊥AB，即∠BEC=∠BED=90°，
∵∠D=35°，
∴∠ABD=90°−∠D=55°，
∴∠ABD=55°；
（2）解：EF∥BC，理由如下；
∵CD平分∠ACB，
∴∠ACD=∠BCD，
∵∠D=∠BCD，
∴∠D=∠ACD，
∴AC∥BD，
∴∠ACB+∠CBD=180°，
∵∠AFE+∠CBD=180°，
∴∠AFE=∠ACB，
∴EF∥BC．
22．（1）如图1，已知：在△ABC中，AB=AC=10，BD平分∠ABC，CD平分∠ACB，过点D作EF∥BC，分别交AB、AC于E、F两点，则图中共有 个等腰三角形；EF与BE、CF之间的数量关系是 ，△AEF的周长是
（2）如图2，若将（1）中“△ABC中，AB=AC=10”改为“若△ABC为不等边三角形，AB=8，AC=10”其余条件不变，则图中共有 个等腰三角形；EF与BE、CF之间的数量关系是什么？证明你的结论，并求出△AEF的周长
（3）已知：如图3，D在△ABC外，AB>AC，且BD平分∠ABC，CD平分ΔABC的外角∠ACG，过点D作DE∥BC，分别交AB、AC于E、F两点，则EF与BE、CF之间又有何数量关系呢？直接写出结论不证明．
【详解】解：（1）BE+CF=EF．
理由如下：
∵AB=AC，
∴∠ABC=∠ACB，
∵BD平分∠ABC，CD平分∠ACB，
∴∠EBD=∠CBD，∠FCD=∠BCD，
∴∠DBC=∠DCB，
∴DB=DC
∵EF∥BC，
∴∠AEF=∠ABC，∠AFE=∠ACB，∠EDB=∠CBD，∠FDC=∠BCD，
∴∠EBD=∠EDB，∠FDC=∠BCD，
∴BE=DE，CF=DF，AE=AF，
∴等腰三角形有△ABC，△AEF，△DEB，△DFC，△BDC共5个，
∴BE+CF=DE+DF=EF，
即BE+CF=EF，
△AEF的周长=AE+EF+AF=AE+BE+AF+FC=AB+AC=20．
故答案为：5；BE+CF=EF；20；
（2）BE+CF=EF，
∵BD平分∠ABC，CD平分∠ACB，
∴∠EBD=∠CBD，∠FCD=∠BCD，
∵EF∥BC，
∴∠EDB=∠CBD，∠FDC=∠BCD，
∴∠EBD=∠EDB，∠FDC=∠BCD，
∴BE=DE，CF=DF，
∴等腰三角形有△BDE，△CFD，
∴BE+CF=DE+DF=EF，即BE+CF=EF．
可得△AEF的周长为18．
（3）BE−CF=EF，
由（1）知BE=ED，
∵EF∥BC，
∴∠EDC=∠DCG=∠ACD，
∴CF=DF，
又∵ED−DF=EF，
∴BE−CF=EF．