初中数学北师大版（2024）八年级上册第一章 勾股定理3 勾股定理的应用图片ppt课件

这是一份初中数学北师大版（2024）八年级上册第一章 勾股定理3 勾股定理的应用图片ppt课件，共40页。

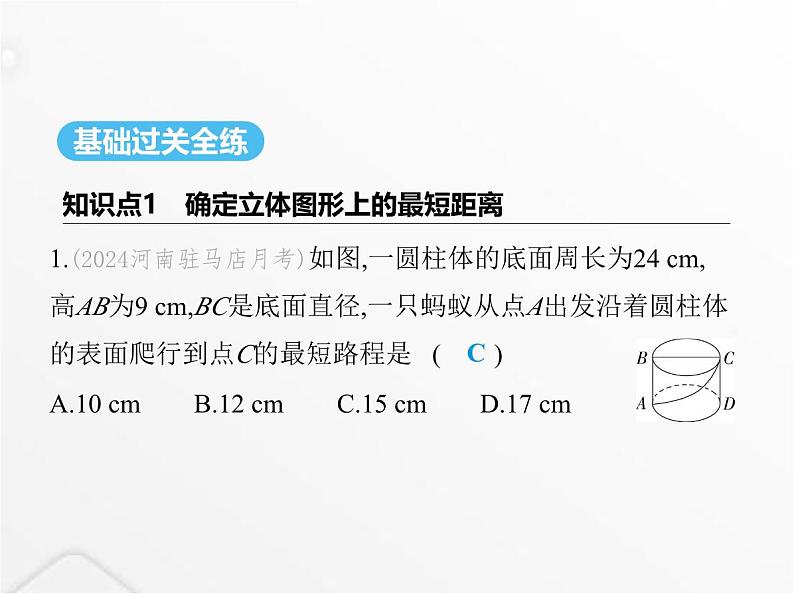
1.(2024河南驻马店月考)如图,一圆柱体的底面周长为24 cm, 高AB为9 cm,BC是底面直径,一只蚂蚁从点A出发沿着圆柱体 的表面爬行到点C的最短路程是 (　    )A.10 cm　　B.12 cm　　C.15 cm　　D.17 cm
解析　圆柱侧面展开图如图所示,连接AC,则AB=CD=9 cm,BC= ×24=12(cm), ∴AC2=122+92=225=152,∴AC=15 cm,故选C.
2.如图所示,正方体的棱长为1,一只蜘蛛从正方体的一个顶 点A爬行到另一个顶点B,则蜘蛛爬行的最短距离的平方是 (　    )A.2　    B.3　    C.4　    D.5
解析　将正方体的前面、上面展开放在同一平面上,连接 AB,如图所示,爬行的最短距离为线段AB的长.由勾股定理得 AB2=(1+1)2+12=5,故选D. 
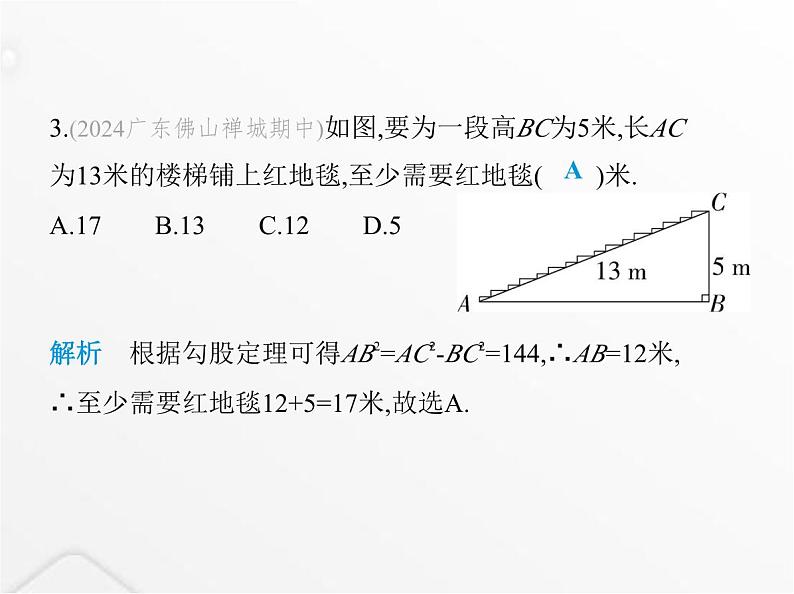
3.(2024广东佛山禅城期中)如图,要为一段高BC为5米,长AC 为13米的楼梯铺上红地毯,至少需要红地毯(　    )米. A.17　    B.13　    C.12　    D.5  
解析　根据勾股定理可得AB2=AC2-BC2=144,∴AB=12米,∴至少需要红地毯12+5=17米,故选A.
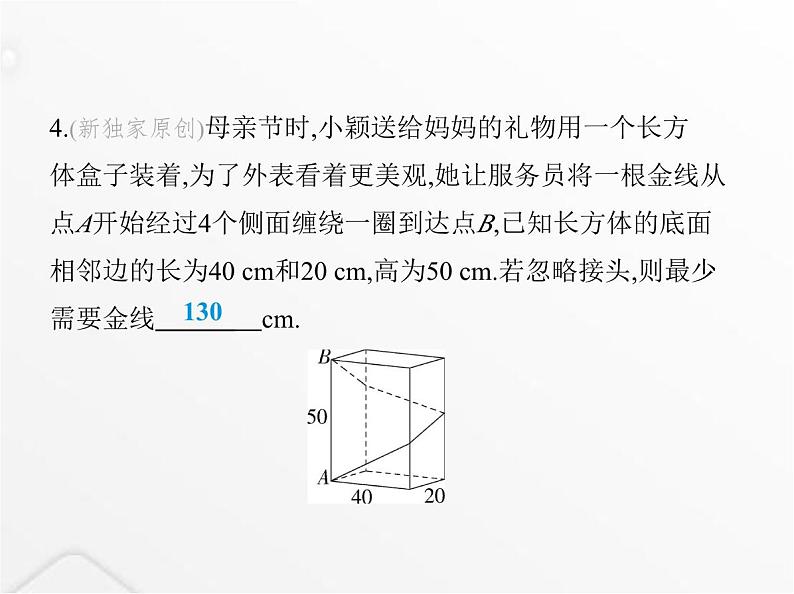
4.(新独家原创)母亲节时,小颖送给妈妈的礼物用一个长方 体盒子装着,为了外表看着更美观,她让服务员将一根金线从 点A开始经过4个侧面缠绕一圈到达点B,已知长方体的底面 相邻边的长为40 cm和20 cm,高为50 cm.若忽略接头,则最少 需要金线　　　    cm. 
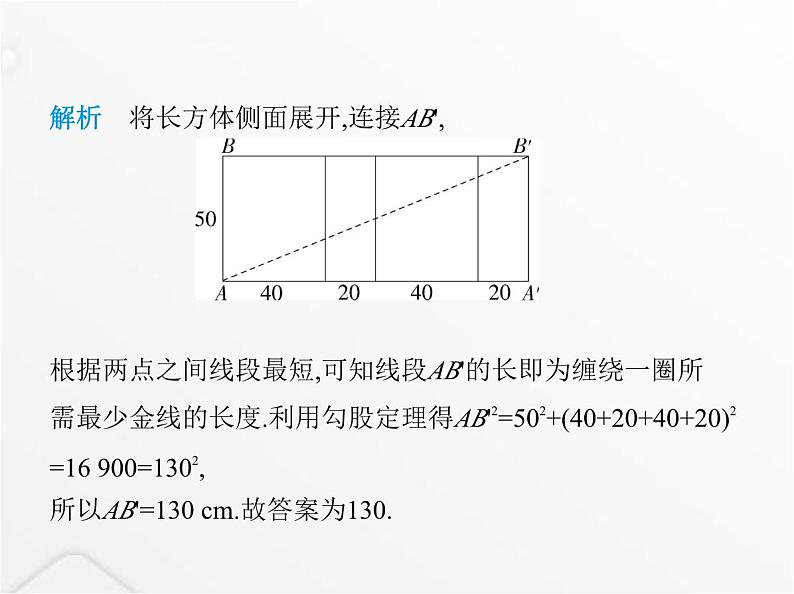
解析　将长方体侧面展开,连接AB', 根据两点之间线段最短,可知线段AB'的长即为缠绕一圈所 需最少金线的长度.利用勾股定理得AB'2=502+(40+20+40+20)2=16 900=1302,
所以AB'=130 cm.故答案为130.
5.(最短路径模型)如图,一只蚂蚁从棱长为6 cm的正方体纸 盒的顶点A处沿纸盒表面爬到点B处.已知BC=2 cm,求蚂蚁爬 行的最短距离是多少. 
解析　将正方体纸盒上方的面展开,连接AB,如图, ∵AD=CD=6 cm,BC=2 cm,∴BD=CD+BC=6+2=8(cm).在Rt△ABD中,AB2=AD2+BD2=62+82=100,∴AB=10 cm.故蚂蚁爬行的最短距离是10 cm.
方法归纳　求立体图形上两点间的最短距离,先把立体图形 展开成平面图形,再确定两点的位置并连线,最后构造直角三 角形,利用勾股定理解决问题.
6.(情境题·数学文化)在我国古代数学名著《算法统宗》里 有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地. 送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢 嬉.良工高士素好奇,算出索长有几?”译文:“有一架秋千,当 它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋 千的踏板就和身高为5尺的人一样高,秋千的绳索始终是拉
直的,试问绳索有多长?”设绳索长为x尺,则所列方程为(        )A.x2=102+(x-5-1)2B.x2=(x-5)2+102C.x2=102+(x+1-5)2D.x2=(x+1)2+102
解析　如图,根据题意可列方程为x2=102+(x+1-5)2,故选C. 
7.(情境题·科学研究)(2022陕西西安铁一中学期中)如图所示, 有一个由传感器控制的灯A,要装在门上方离地高4.5 m的墙 上,任何东西只要移至距该灯5 m及5 m以内时,灯就会自动发 光.一个身高1.5 m的学生走到离墙多远的地方时,灯刚好自 动发光? (　    )A.4 m　　B.3 m　　C.5 m　　D.7 m
解析　当学生走到点D的位置,头顶C与点A的距离是5 m时, 灯刚好自动发光.如图,作CE⊥AB于E,由题意可知BE=CD=1.5 m,AE=AB-BE=4.5-1.5=3 m,AC=5 m.在Rt△ACE中,CE2=AC2-AE2=52-32=16,∴CE=4 m.故这名学生走到离墙4 m远的地方时,灯刚好自动发光,故选A.
8.(新考向·项目式学习试题)(2023山东济南期末)某初中数学 小组欲测量吊车起重臂顶端与地面的距离,下面是他们设计 的项目课题,请你根据下面的表格计算:吊车起重臂顶端A到 地面的距离AF的长.
解析　在Rt△ABG中,AG2=AB2-BG2=102-82=36.∴AG=6.∵FG=BE=1.8,∴AF=AG+GF=6+1.8=7.8(米).答:点A到地面的距离AF的长为7.8米.
9.如图,∠AOB=90°,OA=180 cm,OB=60 cm,一机器人在B处看 见一个小球从点A出发,沿着AO匀速滚向点O,机器人立即从 点B出发,沿着直线BC匀速前进拦截小球,恰好在点C处截住 了小球.如果小球滚动的速度与机器人行走的速度相等,那么 机器人行走的路程BC是多少? 
解析　∵小球滚动的速度与机器人行走的速度相等,运动时 间相等,∴BC=CA,设AC=x cm,则OC=(180-x)cm,在Rt△OBC中,OB=60 cm,由勾股定理可知OB2+OC2=BC2,∴602+(180-x)2=x2,解得x=100.故机器人行走的路程BC是100 cm.
10.(情境题·数学文化)(2020四川巴中中考,8,★★☆)《九章 算术》是我国古代数学的经典著作,书中有一个“折竹抵 地”问题(如图):“今有竹高一丈,末折抵地,去本三尺,问折 者高几何?”意思是:一根竹子,原来高一丈(一丈为十尺),虫 伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,问:原竹子处还有多高的竹子?     (　    ) 
A.4尺　    尺　    C.5尺　    尺
解析　设竹子折断处离地面x尺,则直角三角形的斜边长为(10-x)尺,根据勾股定理得x2+32=(10-x)2,解得x=4.55.所以原竹子处还有4.55尺高的竹子.故选B.
方法归纳　分析数学问题中变量间的等量关系,建立方程或 方程组,通过解方程或方程组,使问题得以解决.本题是根据 勾股定理建立方程模型,体现了数学中的方程思想.
11.(2024广东茂名高州十二校联考期中,14,★★☆)如图,圆 柱的底面半径为  cm,高为18 cm,点A,B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一棉线从点A顺着圆柱 侧面绕3圈到点B,则棉线最短为　　　    cm.
解析　圆柱的侧面展开图如图所示: 用一棉线从点A顺着圆柱侧面绕3圈到点B的最短路线是AC →C'D→D'B,即在圆柱的侧面展开图中,将长方形平均分成3 个小长方形,∴棉线从点A沿着3个长方形的对角线绕到点B 的路线最短.∵圆柱的底面半径为  cm,
∴圆柱的底面周长为2π× =8(cm),即侧面展开图的宽为8 cm.又∵圆柱的高为18 cm,∴小长方形的一条边长是18÷3=6(cm).根据勾股定理求得AC=C'D=BD'=10(cm),∴AC+C'D+D'B=30 cm,故答案为30.
12.(情境题·数学文化)(2024四川成都七中育才学校期中,13, ★★☆)《九章算术》是古代东方数学代表作,书中记载:今 有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几 何?题目大意是:如图(图2为图1的平面示意图),推开双门,双 门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺 =10寸),则AB的长是　　　    寸. 　     
解析　取AB的中点O,过D作DE⊥AB于E,如图所示: 由题意得OA=OB=AD=BC,设OA=OB=AD=BC=r寸,则AB=2r寸,由题意得DE=10寸,OE= CD=1寸,∴AE=(r-1)寸.
在Rt△ADE中,AE2+DE2=AD2,即(r-1)2+102=r2,解得r=50.5,∴2r=101,∴AB=101寸.故答案为101.
13.(2023四川广安中考,15,★★★)如图,圆柱形玻璃杯的杯 高为9 cm,底面周长为16 cm,在杯内壁离杯底4 cm的点A处有 一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿1 cm,且与蜂蜜相对的点B处,则蚂蚁从外壁B处到内壁A处所走 的最短路程为　　　    cm.(杯壁厚度不计) 
解析　如图,将玻璃杯侧面展开(展开图的一半),作B关于直 线EF的对称点B',作B'D⊥AE,交AE延长线于点D,连接AB'. 由题意得DE= BB'=1 cm,AE=9-4=5(cm),∴AD=AE+DE=6 cm,∵底面周长为16 cm,
∴B'D= ×16=8(cm),在Rt△AB'D中,有AB'2=AD2+B'D2=100,∴AB'=10 cm.由两点之间线段最短可知,蚂蚁从外壁B处到内壁A处所走的 最短路程为10 cm,故答案为10.
14.(教材变式·P15T4)(2023陕西咸阳实验中学月考,23,★★ ☆)如图所示的是放在地面上的一个长方体盒子,其中AB=9 cm,BC=6 cm,BF=5 cm,点M在棱AB上,且AM=3 cm,点N是FG 的中点,一只蚂蚁要沿着长方体盒子的外表面从点M爬行到 点N,它需要爬行的最短路程是多少?(盒子底面蚂蚁无法到 达) 
解析　如图1所示,将上底面向前展开,连接MN,蚂蚁爬行的 最短路程显然为线段MN的长.∵AB=9 cm,BC=GF=6 cm,BF=5 cm,∴BM=AB-AM=9-3=6(cm),BN=BF+FN=BF+ FG=5+3=8(cm).在Rt△BMN中,有MN2=BM2+BN2=62+82=100.      
如图2所示,将右侧面向前展开,连接MN,蚂蚁爬行的最短路 程显然为线段MN的长.过N作NP⊥BC于P.∵AB=9 cm,BC=GF=6 cm,BF=5 cm,∴PM=9-3+3=9(cm),NP=5 cm.在Rt△MPN中,有MN2=PM2+PN2=92+52=106.∵100<106,∴图1中的爬行路程最短.∵102=100,∴MN的最小值是10 cm,∴蚂蚁需要爬行的最短路程是10 cm.
15.(运算能力)(分类讨论思想)如图,在Rt△ABC中,∠ACB=90°,AB=5 cm,AC=3 cm,动点P从B出发沿射线BC以2 cm/s的速 度运动,设运动时间为t s.(1)当t=　　　    时,AP平分△ABC的面积.(2)当△ABP为等腰三角形时,求t的值.(3)若点E、F分别为BC、AB上的动点,请直接写出AE+EF的 最小值.      
解析    (1)∵∠ACB=90°,AB=5,AC=3,∴BC2=AB2-AC2=52-32=16,∴BC=4.当BP=CP时,AP平分△ABC的面积,即BP=2t= BC=2,∴t=1,则当t=1时,AP平分△ABC的面积.故答案为1.(2)分三种情况:①如图1,AP=PB,
由题意得AP=BP=2t,∴CP=4-2t,由勾股定理得AP2=AC2+PC2,∴(2t)2=32+(4-2t)2,解得t= .②如图2,AB=BP=5,∴2t=5,∴t= .③如图3,AB=AP,∵∠ACB=90°,∴AC⊥BP,∴BP=2BC=8,∴2t=8,∴t=4.
综上所述,当△ABP为等腰三角形时,t的值是 或 或4.(3) .详解:如图4,延长AC至A',使AC=A'C,连接BA',过点A作AF'⊥A'B于F',在AB上取BF=BF',易知AB与A'B关于直线BC对称,EF=EF',∴AE+EF=AE+EF'=AF',此时AE+EF的值最小,且最小值是AF'的长,∵AC=A'C=3,AB=A'B=5,BC=4,∴△ABA'的面积= ×6×4= ×5AF',
∴AF'= ,∴AE+EF的最小值是 .