初中数学浙教版（2024）八年级上册1.5 三角形全等的判定教课内容ppt课件

这是一份初中数学浙教版（2024）八年级上册1.5 三角形全等的判定教课内容ppt课件，共31页。
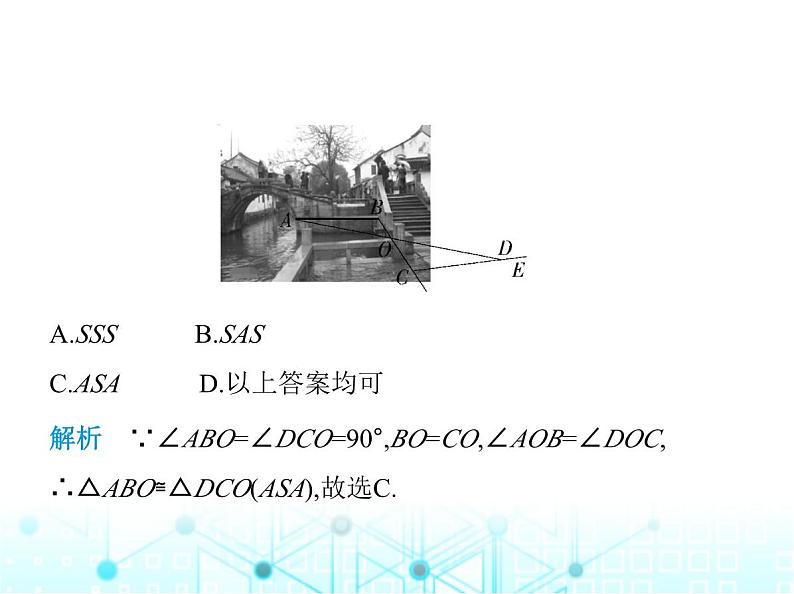
1.(浙江名胜古迹·周庄)(新独家原创)如图所示,假期小华到 浙江省著名景点——周庄旅游,周庄的景物石拱桥引起了小 华的注意,他想知道桥洞右边到街道的距离(图上线段AB的 长度),已知桥壁(AB)垂直于街壁(BO),小华应该如何做呢?聪 明的小华想了想,作了如下图形,延长线段BO到点C,使OC= BO,过点C作直线BC的垂线CE,垂足为C,在CE上找一点D,使 点A、O、D三点在一条直线上,小华说线段CD的长度就是 所求距离,小华证明三角形全等的依据是 (　　)
知识点　基础事实“角边角”或“ASA”
A.SSS　　    　　    D.以上答案均可
解析    ∵∠ABO=∠DCO=90°,BO=CO,∠AOB=∠DOC,∴△ABO≌△DCO(ASA),故选C.
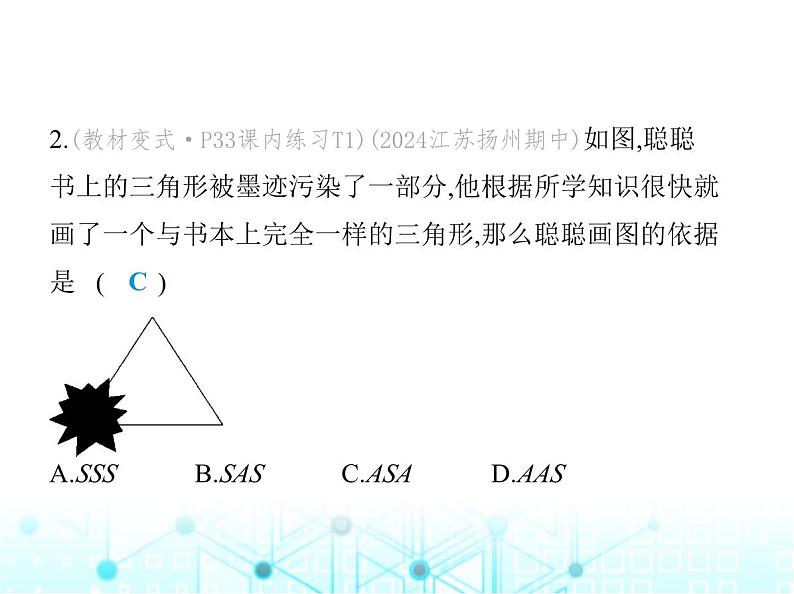
2.(教材变式·P33课内练习T1)(2024江苏扬州期中)如图,聪聪 书上的三角形被墨迹污染了一部分,他根据所学知识很快就 画了一个与书本上完全一样的三角形,那么聪聪画图的依据 是 (　　) A.SSS　　    B.SAS　　    C.ASA　　    D.AAS
解析    由题图可知三角形的两角和它们的夹边是完整的,所 以可以利用“角边角”作出完全一样的三角形.故选C.
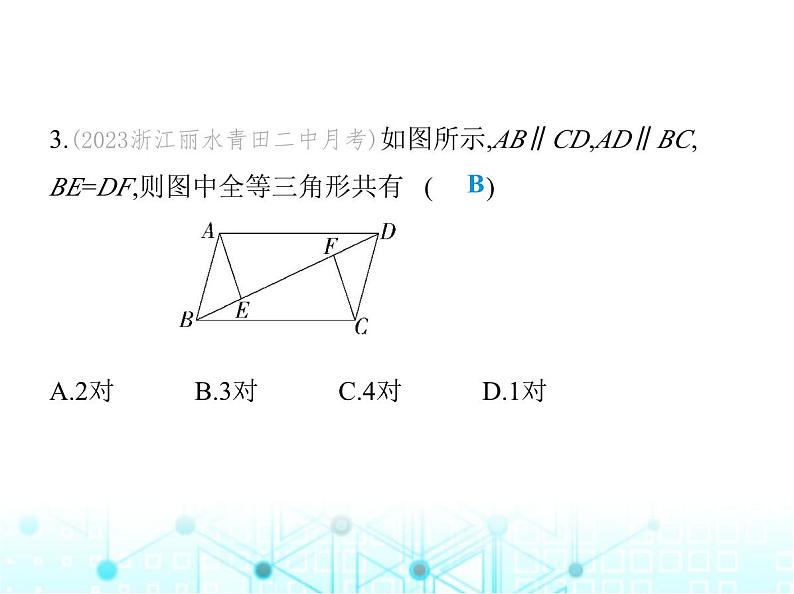
3.(2023浙江丽水青田二中月考)如图所示,AB∥CD,AD∥BC, BE=DF,则图中全等三角形共有 (　　) A.2对　　    B.3对　　    C.4对　　    D.1对
解析    ①∵AB∥CD,AD∥BC,∴∠ABD=∠CDB,∠ADB= ∠CBD,又∵BD=DB,∴△ABD≌△CDB(ASA).②∵△ABD≌ △CDB,∴AB=CD,∵∠ABD=∠CDB,BE=DF,∴△ABE≌ △CDF(SAS).③∵△ABD≌△CDB,△ABE≌△CDF,∴AD= CB,AE=CF,∵BE=DF,∴BE+EF=DF+EF,即BF=DE,∴△AED ≌△CFB(SSS),∴题图中全等三角形共有3对.故选B.
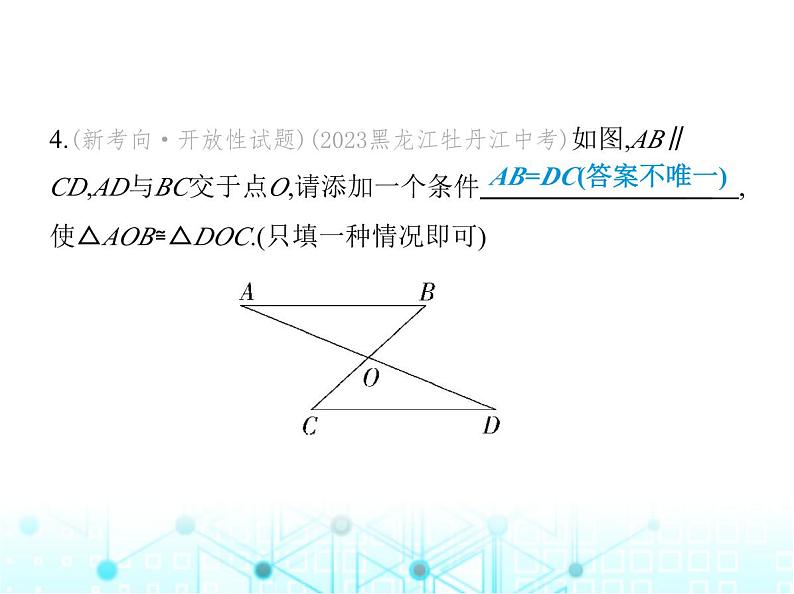
4.(新考向·开放性试题)(2023黑龙江牡丹江中考)如图,AB∥ CD,AD与BC交于点O,请添加一个条件　 　 　    ,使△AOB≌△DOC.(只填一种情况即可)    
AB=DC(答案不唯一)
解析　∵AB∥CD,∴∠A=∠D,∠B=∠C,∴添加条件AB=DC,由ASA即可证明△AOB≌△DOC.故答案为AB=DC(答案不唯一).
5.(手拉手模型)(2023吉林中考)如图,点C在线段BD上,在△ABC 和△DEC中,∠A=∠D,AB=DE,∠B=∠E.求证:AC=DC.  
证明　在△ABC和△DEC中,∴△ABC≌△DEC(ASA),∴AC=DC.
6.(新考法)(2022江苏扬州中考改编,6,★★☆)小明家的一块三角形形状的玻璃坏了,需要重新配一块.小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为△ABC,提供了下列各组元素的数据,配出来的玻璃不一定符合要求的是(　)A.AB,BC,CA　　    B.AB,BC,∠BC.AB,AC,∠B　　    D.∠A,∠B,AB
解析    本题通过实际问题考查全等三角形的判定方法.选项 A,根据SSS一定符合要求;选项B,根据SAS一定符合要求;选项 C,不一定符合要求;选项D,根据ASA一定符合要求.故选C.
7.(新考向·尺规作图)(2023浙江衢州中考,7,★★☆)如图,在 △ABC中,以点A为圆心,适当长为半径画弧,分别交AB,AC于 点D,E.分别以点D,E为圆心,大于 DE的长为半径画弧,交于∠BAC内一点F.连结AF并延长,交BC于点G.连结DG,EG.添 加下列条件,不能使BG=CG成立的是 (　　)A.AB=AC B.AG⊥BCC.∠DGB=∠EGC D.AG=AC
解析    根据题中所给的作图步骤可知,AD=AE,AG是△ABC 的角平分线,所以∠BAG=∠CAG.当AB=AC时,因为∠BAG=∠CAG,且AG=AG,所以△ABG≌△ACG(SAS),所以BG=CG,故A选项不符合题意.当AG⊥BC时,∠AGB=∠AGC=90°,又因为∠BAG=∠CAG,且AG=AG,所以△ABG≌△ACG(ASA),
所以BG=CG,故B选项不符合题意.当∠DGB=∠EGC时,因为AD=AE,∠BAG=∠CAG,AG=AG,所以△ADG≌△AEG(SAS),所以∠AGD=∠AGE,又因为∠DGB=∠EGC,所以∠AGD+∠DGB=∠AGE+∠EGC,即∠AGB=∠AGC,又因为∠AGB+∠AGC=180°,所以∠AGB=∠AGC=90°,
同上面的AG⊥BC可得出BG=CG,故C选项不符合题意.故选D.
8.(2023浙江杭州中学期中,12,★★☆)沛沛沿一段笔直的人 行道行走,边走边欣赏风景,在由C走到D的过程中,通过隔离 带的空隙P,刚好浏览完对面人行道宣传墙上的一条标语,具 体信息如下:如图,AB∥PM∥CD,相邻两平行线间的距离相 等,AC,BD相交于P,PD⊥CD,垂足为D.已知CD=16米,则标语 AB的长度为　　　    .
解析　∵AB∥CD,∴∠ABP=∠CDP,∵PD⊥CD,∴∠CDP=90°,∴∠ABP=90°,∵相邻两平行线间的距离相等, ∴PD=PB,在△ABP和△CDP中, ∴△ABP≌△CDP(ASA),∴AB=CD=16米.
9.(情境题·社会主义先进文化)(2023浙江绍兴模拟,20,★★ ☆)校训是一个学校的灵魂,体现了一所学校的办学传统,代 表着校园文化和教育理念,是人文精神的高度凝练,是学校历 史和文化的积淀.小颖在数学综合实践活动中,利用所学的数 学知识测量学校教学楼上校训牌的高度AP,如图,她先在教 学楼前的D处测得校训牌上端A处的仰角为∠1,然后她后退2 m到达F处,又测得该校训牌下端P处的仰角为∠2,发现∠1 与∠2恰好互余.已知教学楼的高AB=12 m,BD=8.5 m,小颖的 眼睛离地面的距离CD=EF=1.5 m,且A,P,B三点共线,B,D,F三
点共线,AB⊥BF,CD⊥BF,EF⊥BF,垂足分别为B,C,F,校训牌 的顶端与教学楼顶端平齐,请你根据以上信息帮助她求出校 训牌的高度AP. 
解析　如图,延长EC交AB于点G, 由题意易得BG=CD=EF=1.5 m,GC=BD=8.5 m,CE=DF=2 m, ∠AGE=90°,∴GE=GC+CE=10.5 m,∵∠1+∠2=90°,∠1+∠GAC=90°,∴∠2=∠GAC,
∵AB=12 m,∴AG=AB-GB=10.5 m,∴AG=GE,又∵∠AGC=∠EGP=90°,∴△AGC≌△EGP(ASA),∴CG=PG=8.5 m,∴AP=AG-PG=10.5-8.5=2(m),∴校训牌的高度AP为2 m.
10.如图,在△ABC中,∠ABC=60°,△ABC的角平分线AD、CE 交于点O.求证:AC=AE+CD.
证明　如图,在AC上取一点F,使AF=AE,连结OF,∵AD平分∠BAC,∴∠EAO=∠FAO,在△AEO和△AFO中,∴△AEO≌△AFO(SAS),∴∠AOE=∠AOF.∵AD、CE分别平分∠BAC、∠ACB,∴∠ECA+∠DAC= ∠ACB+ ∠BAC= (∠ACB+∠BAC)= ×(180°-60°)=60°,
∴∠AOC=180°-∠ECA-∠DAC=120°,∴∠DOE=∠AOC=120°,∴∠COD=∠AOE=∠AOF=60°,∴∠COF=60°,∴∠COD=∠COF,在△DOC和△FOC中, ∴△DOC≌△FOC(ASA),∴DC=FC,∵AC=AF+FC,∴AC=AE+CD.
11.(推理能力)点D在△ABC的边AB所在的直线上,点E在平 面内,点F在BC的延长线上,∠E=∠BDC,AE=CD,∠EAB+∠DCF=180°.【提出问题】(1)如图1,若点D在BA的延长线上,求证:AD+BC=BE.【类比探究】(2)如图2,若点D在线段AB上,请探究线段AD,BC与BE之间存 在怎样的数量关系,并证明.
【拓展延伸】(3)如图3,若点D在线段AB的延长线上,请直接写出线段AD, BC与BE之间的数量关系.  图1     图2 图3
解析　(1)证明:∵∠EAB+∠DCF=180°,∠BCD+∠DCF= 180°,∴∠EAB=∠BCD,在△EAB和△DCB中, ∴△EAB≌△DCB(ASA),∴BE=BD,AB=BC,∵BD=AD+AB,∴AD+BC=BE.(2)BC-AD=BE.证明如下:∵∠EAB+∠DCF=180°,∠BCD+∠DCF=180°,
∴∠EAB=∠BCD,在△EAB和△DCB中, ∴△EAB≌△DCB(ASA),∴BE=BD,AB=BC,∵BD=AB-AD,∴BC-AD=BE.(3)AD-BC=BE.详解:∵∠EAB+∠DCF=180°,∠DCB+∠DCF=180°,∴∠EAB =∠DCB,