浙教版八年级数学上册专项素养综合练(四)运用勾股定理解决问题课件

这是一份浙教版八年级数学上册专项素养综合练(四)运用勾股定理解决问题课件，共17页。

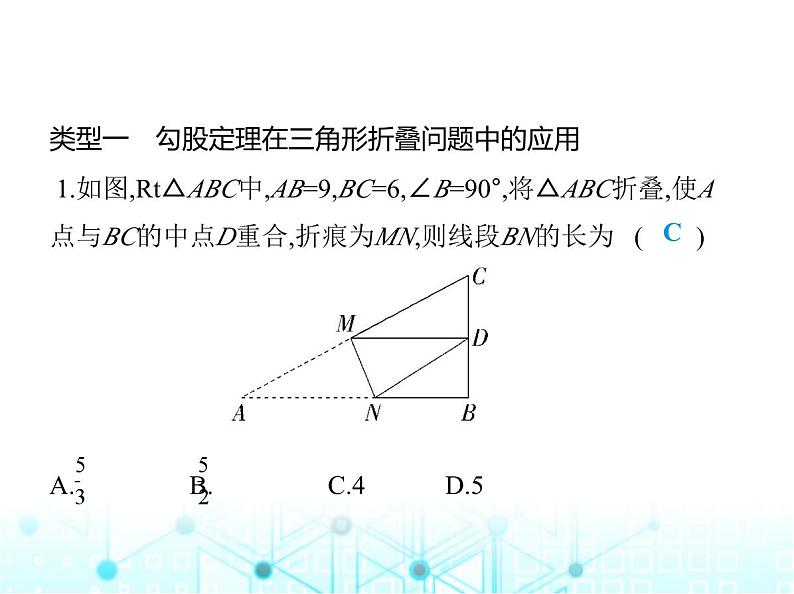
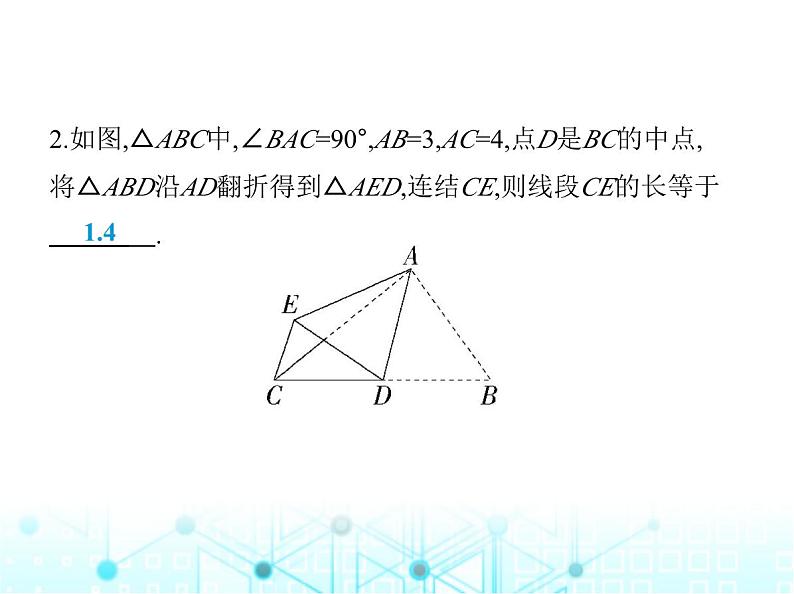
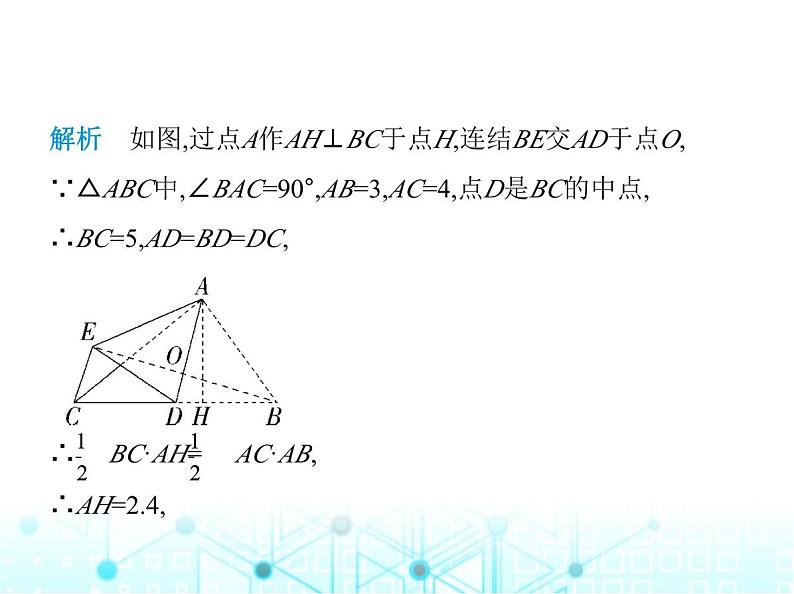
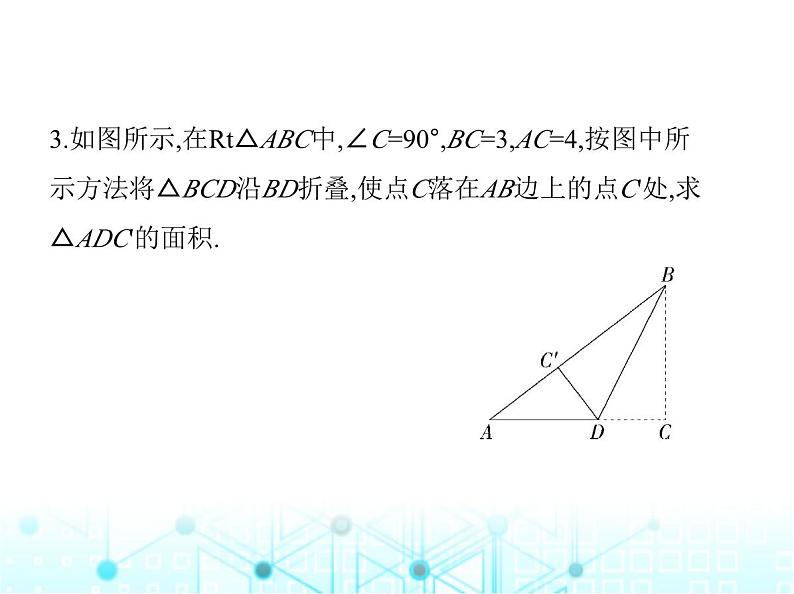
专项素养综合练(四)运用勾股定理解决问题类型一　勾股定理在三角形折叠问题中的应用 1.如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为 (　　)  A. 　　    B. 　　    C.4　　    D.5C解析    设BN=x,由折叠的性质可得DN=AN=9-x,∵D是BC的中点,∴BD=3,在Rt△BDN中,x2+32=(9-x)2,解得x=4.故线段BN的长为4.故选C.2.如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连结CE,则线段CE的长等于　　　    .1.4解析　如图,过点A作AH⊥BC于点H,连结BE交AD于点O,∵△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,∴BC=5,AD=BD=DC, ∴ BC·AH= AC·AB,∴AH=2.4,由折叠可知,OE=OB,AE=AB,DE=DB=DC,∴AD所在直线是BE的垂直平分线,∠ECD=∠CED,∠DEB=∠DBE,∵∠CED+∠ECD+∠DEB+∠EBD=180°,∴∠CED+∠DEB=∠CEB=90°,∴△BCE是直角三角形,∵S△ADB= AD·OB= BD·AH,∴OB=AH=2.4,∴BE=4.8,∵CE2=BC2-BE2=1.96,∴CE=1.4.3.如图所示,在Rt△ABC中,∠C=90°,BC=3,AC=4,按图中所示方法将△BCD沿BD折叠,使点C落在AB边上的点C'处,求△ADC'的面积.  解析　∵∠C=90°,BC=3,AC=4,∴AB= =5,∵将△BCD沿BD折叠,使点C落在AB边上的C'点处,∴∠C=∠BC'D=90°,DC=DC',BC=BC'=3,∴AC'=AB-BC'=2,设DC'=DC=x,则AD=4-x,在Rt△ADC'中,AD2=AC'2+C'D2,∴(4-x)2=22+x2,解得x=1.5,∴DC'=1.5,∵∠AC'D=90°,∴△ADC'的面积= ×AC'·C'D= ×2×1.5=1.5.类型二　勾股定理在四边形折叠问题中的应用4.(2024陕西西安高陵期中)如图,在长方形ABCD中,AB=3,AD=9,将此长方形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为 (　　) A.3　　    B.4　　    C.6　　    D.12C解析　将题中长方形折叠,使点D与点B重合,∴BE=ED.∵AD=AE+DE=AE+BE,∴BE=9-AE,∵四边形ABCD是长方形,∴∠A=90°,在Rt△ABE中,根据勾股定理可知AB2+AE2=BE2,即32+AE2=(9-AE)2,解得AE=4.∴△ABE的面积为3×4÷2=6.故选C.5.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线上D'处.若AB=3,AD=4,则ED的长为 (　　) A. 　　    B.3　　    C.1　　    D. A解析　∵四边形ABCD是长方形,∴∠D=90°,AB=CD=3,在Rt△ACD中,AC= =5,根据折叠可得△DEC≌△D'EC,∴D'C=DC=3,DE=D'E,∠ED'C=∠D,∴AD'=AC-CD'=2,设ED=x,则D'E=x,AE=4-x,易知∠AD'E=90°,在Rt△AED'中,AD'2+ED'2=AE2,即22+x2=(4-x)2,解得x= .故选A.6.(方程思想)如图,长方形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折得到△EBP,PE与CD相交于点O,且OE=OD,BE与CD相交于点F.(1)求证:OP=OF.(2)求AP的长.  解析　(1)证明:∵四边形ABCD是长方形,∴∠D=∠A=90°,由翻折的性质可知∠E=∠A=90°,∴∠D=∠E=90°,在△ODP和△OEF中, ∴△ODP≌△OEF(ASA),∴OP=OF.(2)∵△ODP≌△OEF,∴OP=OF,PD=FE.∵OD=OE,∴DF=EP.∵四边形ABCD是长方形,∴∠C=90°,AD=BC=6,CD=AB=8,由翻折得EP=AP,设AP=EP=DF=x,则PD=EF=6-x,CF=8-x,∴BF=8-(6-x)=2+x,在Rt△FCB中,根据勾股定理得BC2+CF2=BF2,即62+(8-x)2=(2+x)2,解得x=4.8, ∴AP=4.8.