





还剩7页未读,
继续阅读
所属成套资源:全套浙教版八年级数学上册专项素养综合练课件
成套系列资料,整套一键下载
浙教版八年级数学上册专项素养综合练(五)数学文化课件
展开
这是一份浙教版八年级数学上册专项素养综合练(五)数学文化课件,共14页。
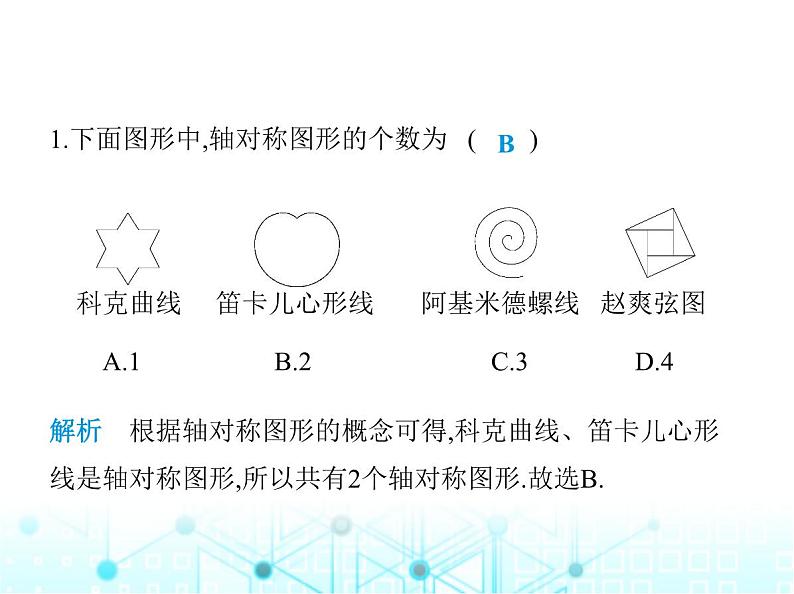
专项素养综合练(五)数学文化1.下面图形中,轴对称图形的个数为 ( ) 科克曲线 笛卡儿心形线 阿基米德螺线 赵爽弦图 A.1 B.2 C.3 D.4 B解析 根据轴对称图形的概念可得,科克曲线、笛卡儿心形 线是轴对称图形,所以共有2个轴对称图形.故选B.2.(2023四川泸州中考)《九章算术》是中国古代重要的数学 著作,该著作中给出了勾股数a,b,c的计算公式:a= (m2-n2),b=mn,c= (m2+n2),其中m>n>0,m,n是互质的奇数.下列四组勾股数中,不能由该勾股数计算公式直接得出的是 ( )A.3,4,5 B.5,12,13C.6,8,10 D.7,24,25C解析 ∵当m=3,n=1时,a= (m2-n2)= ×(32-12)=4,b=mn=3×1=3,c= (m2+n2)= ×(32+12)=5,∴选项A不符合题意;∵当m=5,n=1时,a= (m2-n2)= ×(52-12)=12,b=mn=5×1=5,c= (m2+n2)= ×(52+12)=13,∴选项B不符合题意;∵当m=7,n=1时,a= (m2-n2)= ×(72-12)=24,b=mn=7×1=7,c= (m2+n2)= ×(72+12)=25,∴选项D不符合题意;∵没有符合条件的m,n使a,b,c分别为6,8,10, ∴选项C符合题意.故选C.3.(2023安徽中考)清初数学家梅文鼎在著作《平三角举要》 中,对南宋数学家秦九韶提出的计算三角形面积的“三斜求 积术”给出了一个完整的证明,证明过程中创造性地设计直 角三角形,得出了一个结论:如图,AD是锐角△ABC的高,则BD = .当AB=7,BC=6,AC=5时,CD= . 1解析 ∵BD= ,AB=7,BC=6,AC=5,∴BD= × =5,∴CD=BC-BD=6-5=1.故答案为1.4.“三等分角”大约是在公元前五世纪由古希腊人提出来 的,借助如图所示的“三等分角仪”能三等分任一角.这个三 等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并 可绕O转动,C点固定,OC=CD=DE,点D、E可在槽中滑动.若 ∠BDE=75°,则∠CDE的度数是 . 80°解析 ∵OC=CD=DE,∴∠O=∠CDO,∠DCE=∠DEC,∵∠DCE=∠O+∠CDO=2∠O,∴∠DEC=2∠O,∴∠BDE=∠O+∠DEC=3∠O=75°,∴∠O=25°,∴∠DCE=∠DEC=50°,∴∠CDE=80°.5.(2022甘肃武威中考)中国清朝末期的几何作图教科书《最 新中学教科书用器画》中记载了大量几何作图题,所有内容 均用浅近的文言文表述,第一编记载了这样一道几何作图题:(1)根据以上信息,请你用不带刻度的直尺和圆规,在图中完 成作图(保留作图痕迹,不写作法).(2)根据(1)中作图,直接写出∠DBG,∠GBF,∠FBE的大小关 系. 解析 (1)如图. (2)∠DBG=∠GBF=∠FBE.详解:连结DF,EG,如图所示,则BD=BF=DF,BE=BG=EG,即△BDF和△BEG均为等边三角形,∴∠DBF=∠EBG=60°,∵∠ABC=90°,∴∠DBG=∠GBF=∠FBE=30°.
专项素养综合练(五)数学文化1.下面图形中,轴对称图形的个数为 ( ) 科克曲线 笛卡儿心形线 阿基米德螺线 赵爽弦图 A.1 B.2 C.3 D.4 B解析 根据轴对称图形的概念可得,科克曲线、笛卡儿心形 线是轴对称图形,所以共有2个轴对称图形.故选B.2.(2023四川泸州中考)《九章算术》是中国古代重要的数学 著作,该著作中给出了勾股数a,b,c的计算公式:a= (m2-n2),b=mn,c= (m2+n2),其中m>n>0,m,n是互质的奇数.下列四组勾股数中,不能由该勾股数计算公式直接得出的是 ( )A.3,4,5 B.5,12,13C.6,8,10 D.7,24,25C解析 ∵当m=3,n=1时,a= (m2-n2)= ×(32-12)=4,b=mn=3×1=3,c= (m2+n2)= ×(32+12)=5,∴选项A不符合题意;∵当m=5,n=1时,a= (m2-n2)= ×(52-12)=12,b=mn=5×1=5,c= (m2+n2)= ×(52+12)=13,∴选项B不符合题意;∵当m=7,n=1时,a= (m2-n2)= ×(72-12)=24,b=mn=7×1=7,c= (m2+n2)= ×(72+12)=25,∴选项D不符合题意;∵没有符合条件的m,n使a,b,c分别为6,8,10, ∴选项C符合题意.故选C.3.(2023安徽中考)清初数学家梅文鼎在著作《平三角举要》 中,对南宋数学家秦九韶提出的计算三角形面积的“三斜求 积术”给出了一个完整的证明,证明过程中创造性地设计直 角三角形,得出了一个结论:如图,AD是锐角△ABC的高,则BD = .当AB=7,BC=6,AC=5时,CD= . 1解析 ∵BD= ,AB=7,BC=6,AC=5,∴BD= × =5,∴CD=BC-BD=6-5=1.故答案为1.4.“三等分角”大约是在公元前五世纪由古希腊人提出来 的,借助如图所示的“三等分角仪”能三等分任一角.这个三 等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并 可绕O转动,C点固定,OC=CD=DE,点D、E可在槽中滑动.若 ∠BDE=75°,则∠CDE的度数是 . 80°解析 ∵OC=CD=DE,∴∠O=∠CDO,∠DCE=∠DEC,∵∠DCE=∠O+∠CDO=2∠O,∴∠DEC=2∠O,∴∠BDE=∠O+∠DEC=3∠O=75°,∴∠O=25°,∴∠DCE=∠DEC=50°,∴∠CDE=80°.5.(2022甘肃武威中考)中国清朝末期的几何作图教科书《最 新中学教科书用器画》中记载了大量几何作图题,所有内容 均用浅近的文言文表述,第一编记载了这样一道几何作图题:(1)根据以上信息,请你用不带刻度的直尺和圆规,在图中完 成作图(保留作图痕迹,不写作法).(2)根据(1)中作图,直接写出∠DBG,∠GBF,∠FBE的大小关 系. 解析 (1)如图. (2)∠DBG=∠GBF=∠FBE.详解:连结DF,EG,如图所示,则BD=BF=DF,BE=BG=EG,即△BDF和△BEG均为等边三角形,∴∠DBF=∠EBG=60°,∵∠ABC=90°,∴∠DBG=∠GBF=∠FBE=30°.
相关资料
更多









