湖南省益阳市资阳区多校联考2024-2025学年九年级上学期开学考试数学试题（原卷版）

这是一份湖南省益阳市资阳区多校联考2024-2025学年九年级上学期开学考试数学试题（原卷版），共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本题共10个小题，每小题3分，满分30分）
1. 以下列各组数为边长，不能构成直角三角形的是（ ）
A. 3，4，5B. 9，12，15C. ，2，D. 0.3，0.4，0.5
2. 某市在开展“红心颂党恩，喜迎二十大”主题活动演讲比赛中，成绩在95分以上的选手有8人，频率为0.2，则参加比赛的选手共有（ ）
A. 16人B. 40人C. 80人D. 20人
3. 下列说法正确的是（ ）
A. 对角线互相垂直的四边形是菱形B. 矩形的对角线互相垂直
C. 一组对边平行的四边形是平行四边形D. 四边相等的四边形是菱形
4. 关于一次函数的图象和性质，下列说法正确的是（ ）
A. 随的增大而增大B. 图象经过第三象限
C. 图象经过点D. 图象与轴的交点是
5. 下列说法正确的是（ ）
A. 两个锐角对应相等的两个直角三角形全等
B. 频数与频率相等
C. 一次函数都是正比例函数
D. 菱形既轴对称图形又是中心对称图形
6. 在平面直角坐标系的第二象限内有一点P，点P到x轴的距离为2，到y轴的距离为3，则点P的坐标是（ ）
A. B. C. D.
7. 如图，已知，P是平分线上一点，，交于点C，，垂足为点D，且，则的长为（ ）

A. 2B. C. 3D. 4
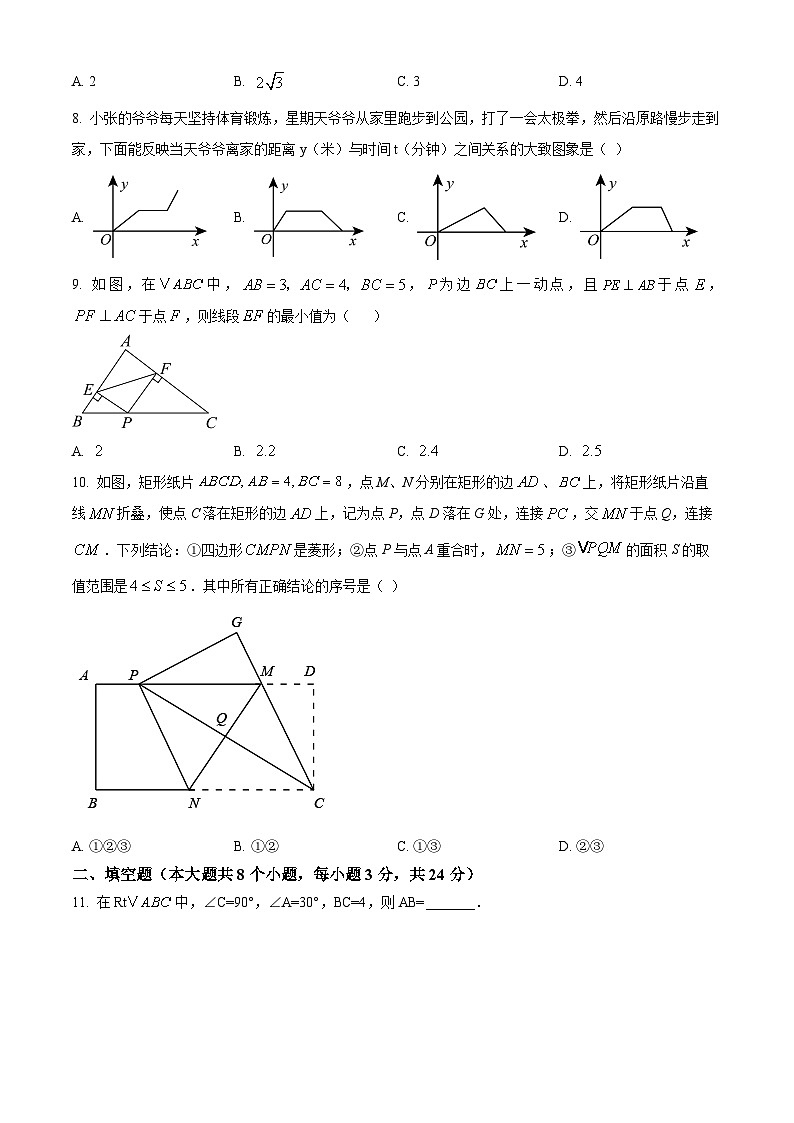
8. 小张的爷爷每天坚持体育锻炼，星期天爷爷从家里跑步到公园，打了一会太极拳，然后沿原路慢步走到家，下面能反映当天爷爷离家的距离y（米）与时间t（分钟）之间关系的大致图象是（ ）
A. B. C. D.
9. 如图，在中，，为边上一动点，且于点，于点，则线段的最小值为（ ）
A. B. C. D.
10. 如图，矩形纸片，点M、N分别在矩形的边、上，将矩形纸片沿直线折叠，使点C落在矩形的边上，记为点P，点D落在G处，连接，交于点Q，连接．下列结论：①四边形是菱形；②点P与点A重合时，；③的面积S的取值范围是．其中所有正确结论的序号是（ ）
A. ①②③B. ①②C. ①③D. ②③
二、填空题（本大题共8个小题，每小题3分，共24分）
11. 在Rt中，∠C=90°，∠A=30°，BC=4，则AB=_______．

12. 一个正多边形的内角和为，则这个正多边形的每一个外角等于______度．
13. 在平面直角坐标系中，点关于轴对称的点的坐标为_____．
14. 如图，在中，，点D是的中点，，，则______．
15. 将一次函数的图象向上平移个单位，得到的一次函数的表达式是__________．
16. 如图，在△ABC中，∠C＝90°，AC＝6，DC，BD平分∠ABC，则点D到AB的距离为 ___．
17. 如图，在中，分别是的中点，点在上，且，若，则的长为_____．
18. 如图，在平面直角坐标系中，点、、……都在x轴上，点，，，……都在直线上，，，，，都是等腰直角三角形，且，则点的坐标是___________．
三、解答题（本题共8个小题，共66分）
19. 如图，四边形中，，，，，，计算四边形的面积．
20. 阅读下列一段文字，然后回答下列问题，已知在平面内两点，，其两点间的距离．同时，当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为或．
（1）已知，，试求A、B两点间距离；
（2）已知一个三角形各顶点坐标为、、，请判定此三角形形状，并说明理由．
21. 如图，已知是四边形各边的中点．
（1）证明：四边形为平行四边形；
（2）若四边形是矩形，且其面积是，求四边形的面积．
22. 2015年3月30日是全国中小学生安全教育日，学校为加强学生的安全意识，组织了全校1500名学生参加安全知识竞赛，从中抽取了部分学生成绩（得分取正整数，满分为100分）进行统计．请根据尚未完成的频率分布表和频数分布直方图，解答下列问题：
频率分布表

（1）这次抽取了_________名学生的竞赛成绩进行统计，其中：_________，_________；
（2）补全频数分布直方图；
（3）若成绩在70分以下（含70分）的学生为安全意识不强，有待进一步加强安全教育，则该校安全意识不强的学生约有多少人？
23. 某省疾控中心将一批10万剂疫苗运往A，B两城市，根据预算，运往A城的费用为800元/万剂，运往B城的费用为600元/万剂．结合A城的疫苗预约情况，A城的需求量不低于4万剂，设运输这批10万剂疫苗的总费用为y（元），运往A城x（万剂）．
（1）求y与x函数关系式；
（2）在满足A城市最低需求量的情况下，求运输费用最少的方案，最少费用是多少？
24. 如图，在平面直角坐标系xOy中，直线：与y轴交于点Q，且与直线：相交于点P，其中点P纵坐标为1．
（1）求点P的坐标及的值；
（2）求△PQO的面积；
（3）直接写出不等式的解集．
25. 如图，已知中，，点为边上一动点，四边形是正方形，连接，正方形对角线交于点．
（1）求证：；
（2）求证：；
（3）若，求的值．
26. 如图，已知直线与坐标轴交于B，C两点，点A是x轴正半轴上一点，并且，点F是线段上一动点（不与端点重合），过点F作轴，交BC于E．

（1）求所在直线的解析式；
（2）若轴于D，且点D的坐标为，请用含m的代数式表示与的长；
（3）在x轴上是否存在一点P，使得为等腰直角三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．分数段
频数
频率
16
008
40
0.2
50
0.25
m
0.35
24
n