











所属成套资源:人教版九年级数学下册 课件+教学设计+导学案+分层练习+知识清单+单元知识解读+测试卷+单元复习课件
初中数学28.1 锐角三角函数一等奖教学ppt课件
展开这是一份初中数学28.1 锐角三角函数一等奖教学ppt课件,文件包含人教版数学九年级下册281锐角三角函数第2课时课件pptx、281锐角三角函数第2课时教学设计docx、281锐角三角函数第2课时导学案docx等3份课件配套教学资源,其中PPT共35页, 欢迎下载使用。
1.通过探究使学生知道当直角三角形的锐角固定时,它的邻边与斜边的比,对边与邻边的比都是一个固定值,引出余弦、正切的概念;2.理解余弦、正切的概念并能根据概念正确进行计算;3.经历余弦、正切概念的发现与学习过程,培养学生由特殊到一般的归纳推理能力.引导学生体验数学活动,探索与发现新知识,使学生会用数学的思维方式去思考、发现、总结、验证.
【提问】简述正弦的概念?
如图,在直角三角形中,我们把锐角A的对边与斜边的比叫做∠A的正弦,记作:sinA.
【易错点提示】1.sinA是一个比值(数值,无单位)大小只与∠A的大小有关,而与直角三角形的边长无关不表示“sin”乘“A”.
【小组讨论】在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定,此时∠A的对边与斜边的比是否也随之确定呢?
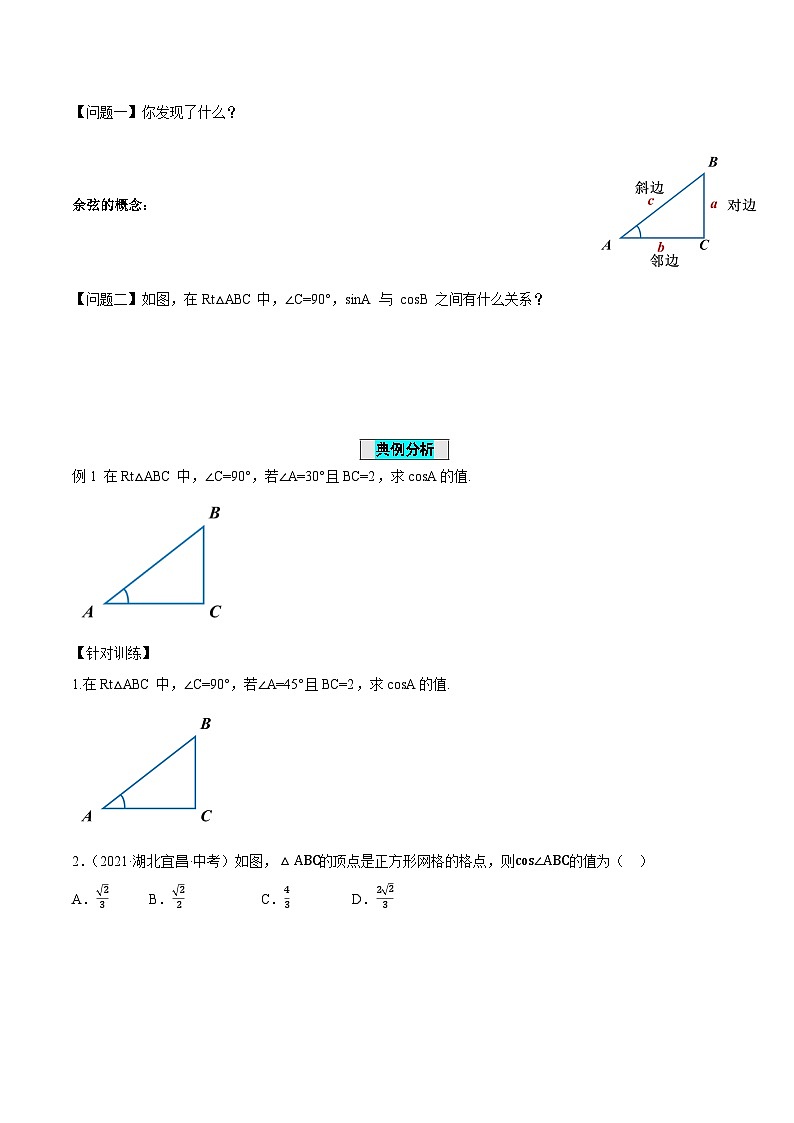
【问题一】你发现了什么?
在直角三角形中,当锐角A的度数一定时,它的邻边与斜边的比是一个固定值,且比值的大小与直角三角形大小无关.
如图,在直角三角形中,我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作csA,
【问题二】如图,在Rt△ABC中,∠C=90°,sinA 与 csB 之间有什么关系?
sinA = csB
【补充】对于任意锐角α,有csα=sin(90°-α) 从而有sinα= cs(90°-α)
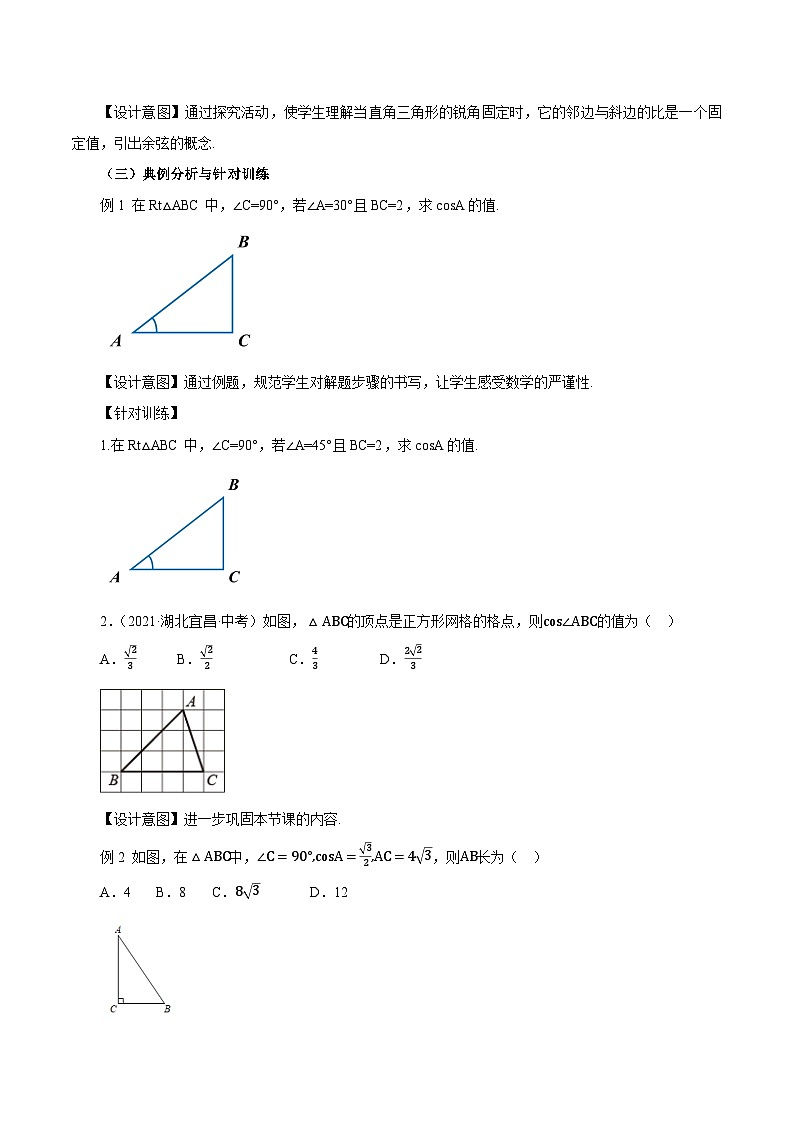
例1 在Rt△ABC中,∠C=90°,若∠A=30°且BC=2,求csA的值.
1.在Rt△ABC中,∠C=90°,若∠A=45°且BC=2,求csA的值.
【小组讨论】在Rt△ABC中,∠C=90°°,当锐角A确定时,∠A的对边与斜边的比、邻边与斜边的比就随之确定,此时∠A的对边与邻边的比是否也随之确定呢?
【问题三】你发现了什么?
在直角三角形中,当锐角A的度数一定时,它的对边与邻边的比是一个固定值,且比值的大小与直角三角形大小无关.
如图,在直角三角形中,我们把锐角A的对边与邻边的比叫做∠A 的正切,记作 tanA,
在直角三角形中,对于锐角A的每一个确定的值,sinA、csA、tanA都有唯一的确定的值与它对应,所以把锐角A的正弦、余弦、正切叫做∠A的锐角三角函数.
例3 在Rt△ABC中,∠C=90°,若∠A=30°且BC=2,求tanA的值.
3. 在Rt△ABC中,∠C=90°,AC=2,BC=3. sinA=_____,csA=_____,tanA=_____, sinB=_____,csB=_____,tanB=_____.
1.通过本节课的学习,你学会了哪些知识?2. 简述余弦、正切的概念? 3.简述锐角三角函数的概念?
P65:练习P68:习题28.1 第1题
相关课件
这是一份人教版(2024)九年级下册29.2 三视图教学课件ppt,文件包含人教版数学九年级下册292投影第2课时课件pptx、292视图第2课时教学设计docx、292视图第2课时导学案docx等3份课件配套教学资源,其中PPT共30页, 欢迎下载使用。
这是一份人教版(2024)29.1 投影评优课教学课件ppt,文件包含人教版数学九年级下册291投影第2课时课件pptx、291投影第2课时教学设计docx、291投影第2课时导学案docx等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
这是一份人教版(2024)九年级下册28.1 锐角三角函数精品教学课件ppt,文件包含人教版数学九年级下册281锐角三角函数第4课时课件pptx、281锐角三角函数第4课时教学设计docx、281锐角三角函数第4课时导学案docx等3份课件配套教学资源,其中PPT共24页, 欢迎下载使用。














