人教版数学九年级下册 第二十八章 锐角三角函 章末总结课件

这是一份人教版数学九年级下册 第二十八章 锐角三角函 章末总结课件，共52页。

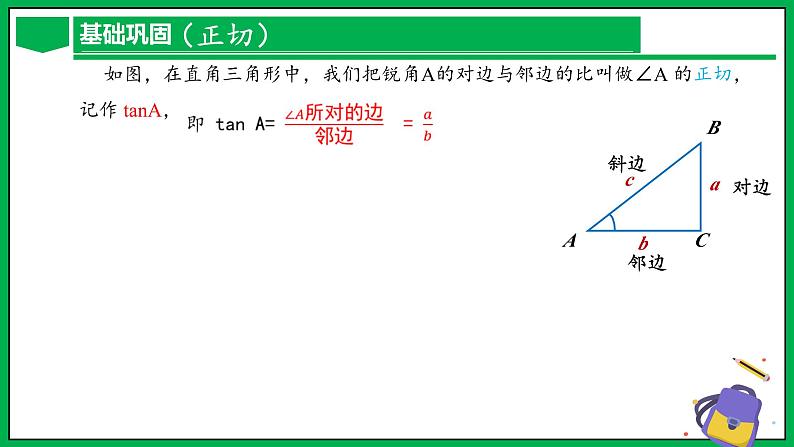
章末总结人教版数学九年级下册目 录1 章节简介2 基础巩固3 热考题型4 直击中考 学习目标1）理解锐角三角函数的定义，掌握特殊锐角(30°，45°，60°的三角函数值，并会进行计算.2）掌握直角三角形边角之间的关系，会解直角三角形.3）利用解直角三角形的知识解决简单的实际问题.4）进一步培养学生分析问题和解决问题的能力. 锐角三角函数为解直角三角形的基础，及提供了有效的工具.相似三角形的知识是学习锐角三角函数的直接基础，勾股定理等内容也是解直角三角形时经常使用的数学结论，因此本章与“勾股定理”和“相似”两章有着密切关系. 如图，在Rt△ABC中，∠C=90°，我们把锐角A的对边与斜边的比叫做∠A的正弦，记作：sinA. 正弦的表示：1）sinA、sin40 °、sinα（省去角的符号）2）sin∠ABC 、sin∠1 （不能省去角的符号） （正弦） 如图，在直角三角形中，我们把锐角A的邻边与斜边的比叫做∠A的余弦，记作cosA， （余弦）　 如图，在直角三角形中，我们把锐角A的对边与邻边的比叫做∠A 的正切，记作 tanA， （正切）30°、45°、60°角的正弦值、余弦值和正切值如下表：1（特殊角的锐角三角函数）1）α为锐角，对于sinα与tanα，角度越大，函数值越 ；对于cosα，角度越大，函数值越 .大小2）互余的两角之间的三角函数关系：若∠A+∠B=90°，则sinA cosB，即一个锐角的正弦值等于这个角的余角的余弦值.cosA sinB，即一个锐角的余弦值等于这个角的余角的正弦值.tanA·tanB = ，即一个锐角的正切值与这个角的余角的正切值互为倒数.==1（特殊角的锐角三角函数）利用计算器求锐角三角函数值的方法：1）当锐角的大小以度为单位时，可先按 ， ， 键，然后输入角度值(可以是整数，也可以是小数)，最后按 键，就可以在显示屏上显示出结果；2）当锐角的大小以度、分、秒为单位时要借助 键计算，按键顺序是： (或 、 )、度数、 、分数、 、秒数、 、 .sincostan=.,,,sincostan.,,,.,,,.,,,=注意：1）不同的计算器操作步骤可能有所不同.（利用计算器求锐角三角函数值）在解直角三角形的过程中，一般要用到下面一些关系：1）直角三角形的五个元素：2）三边之间的关系：3）两锐角之间的关系：4）边角之间的关系：∠A＋∠B＝90°    边：a、b、c，角：∠A、∠B（解直角三角形）解直角三角形常见类型及方法：∠B=90°－∠A∠B=90°－∠A（解直角三角形）利用解直角三角形解决实际问题的一般步骤：1.将实际问题抽象为数学问题. 画出平面图形，转化为解直角三角形的问题；2.根据条件的特点，适当选用锐角三角函数等去解直角三角形；3.得到数学问题的答案；4.得到实际问题的答案.（利用解直角三角形解决实际问题）在视线与水平线所成的角中规定:1)视线在水平线上方的叫做仰角，2)视线在水平线下方的叫做俯角.以正南或正北方向为准，正南或正北方向线与目标方向线构成的小于90°的角，叫做方位角.（利用解直角三角形解决实际问题） 坡度是地表单元陡缓的程度，通常把坡面的垂直高度h和水平距离l的比叫做坡度（或叫做坡比）用字母i表示.【即坡角的正切值（可写作：i=tan坡角）】（利用解直角三角形解决实际问题）  B  3  二（利用正弦值求解） 三（求余弦值） 84  四（利用余弦值求解）  五（求正切值）2. 在Rt△ABC中，∠C＝90°，AC=2，BC=3. sinA=_____，cosA=_____，tanA=_____， sinB=_____，cosB=_____，tanB=_____.      五（求正切值）  六（利用正切值求解）  六（利用正切值求解） 七（利用特殊角三角函数值求解） 七（利用特殊角三角函数值求解） 3 七（利用特殊角三角函数值求解）   八（锐角三角函数增减性）1．如图，在△ABC中，∠C=90°，∠B=42°37'，BC=8，若用科学计算器求AC的长，则下列按键顺序正确的是（  ）九（利用计算器求锐角三角函数值）    十（解直角三角形）  十（解直角三角形） 【详解】在Rt△AOB中，∠AOB=90°，AB=300米，BO=AB•sinα=300sinα米．故选A．2 南洞庭大桥是南益高速公路上的重要桥梁，小芳同学在校外实践活动中对此开展测量活动．如图，在桥外一点A测得大桥主架与水面的交汇点C的俯角为α，大桥主架的顶端D的仰角为β，已知测量点与大桥主架的水平距离AB＝a，则此时大桥主架顶端离水面的高CD为___________ 十一（利用解直角三角形解决实际问题）  十一（利用解直角三角形解决实际问题）  十一（利用解直角三角形解决实际问题） 在中考中，直角三角形在中考常结合勾股定理、面积法在选择题、填空题考查；锐角三角形函数常在选择题、填空题考查，并且结合实际问题考查。                   【详解】解：如图，过点C作水平线与AB的延长线交于点D，则AD⊥CD，∴∠BCD=α，∠ACD=45°．在Rt△CDB中，CD=mcosα，BD=msinα，在Rt△CDA中，AD=CD×tan45°=m×cosα×tan45°=mcosα，∴AB=AD-BD=（mcosα-msinα）=m（cosα-sinα）．故选：A．      人教版初中数学九年级下册