人教A版 (2019)选择性必修 第二册4.1 数列的概念教案设计

这是一份人教A版 (2019)选择性必修 第二册4.1 数列的概念教案设计，共7页。教案主要包含了教学目标，教学重点，学法与教学用具，教学过程，教学反思等内容，欢迎下载使用。
4.1.1 数列的概念与通项公式
一、教学目标
1、正确理解数列的概念，理解数列的通项公式，感受数列是刻画自然规律的数学模型.
2、初步掌握数列的通项公式，正确理解数列的前项和与通项的关系，了解简单的递推数列.
二、教学重点、难点
重点：认知数列的概念和通项公式，数列的前项和与通项的关系.
难点：数列的前项和与通项的关系的应用.
三、学法与教学用具
1、学法：学生在老师的引导下，通过阅读教材，自主学习、思考、交流、讨论和概括，从而完成本节课的教学目标.
2、教学用具：多媒体设备等
四、教学过程
（一）创设情景，揭示课题
【情景一】图中的图形代表什么？
【发现】可以是点数1,6,11,16.
【情景二】下列数据可以表示什么？
【发现】可以是U盘的容量大小，也可以代表电脑显卡的数值，…
【情景三】以下数字可以代表什么：
（1）1,2,3,4,5,6,7
（2）12,24,36,48，…
（3）
（4）10,200,3000,40000，…
（5）5,55,555,5555，…
【情景四】猜一猜下列表格中的每一格表示什么？
【发现】无论是记录自己在一个学期中的数学考试成绩，还是记录自己每一个月的体重，还是记录种植的小树在每一年同一时刻的高度，…，都会与数字有关.
【问题】表达一类事物，或者记录某一过程等等，这些按照一定顺序排列的数如何用数学的角度进行研究？
（二）阅读精要，研讨新知
阅读课本～ （预定用时2-3分钟），记忆相关概念.
【数列及其概念】
【提醒】强化符号，以及
【情景三的通项公式的认知】
（1）数列1,2,3,4,5,6,7的通项公式为
（2）12,24,36,48，…的通项公式为
（3）的通项公式为
（4）10,200,3000,40000，…的通项公式为
（5）5,55,555,5555，…的通项公式为（可以留作课后思考）
【例题研讨】阅读领悟课本例1、例2、例3（用时约为3分钟，教师作出准确的评析.）
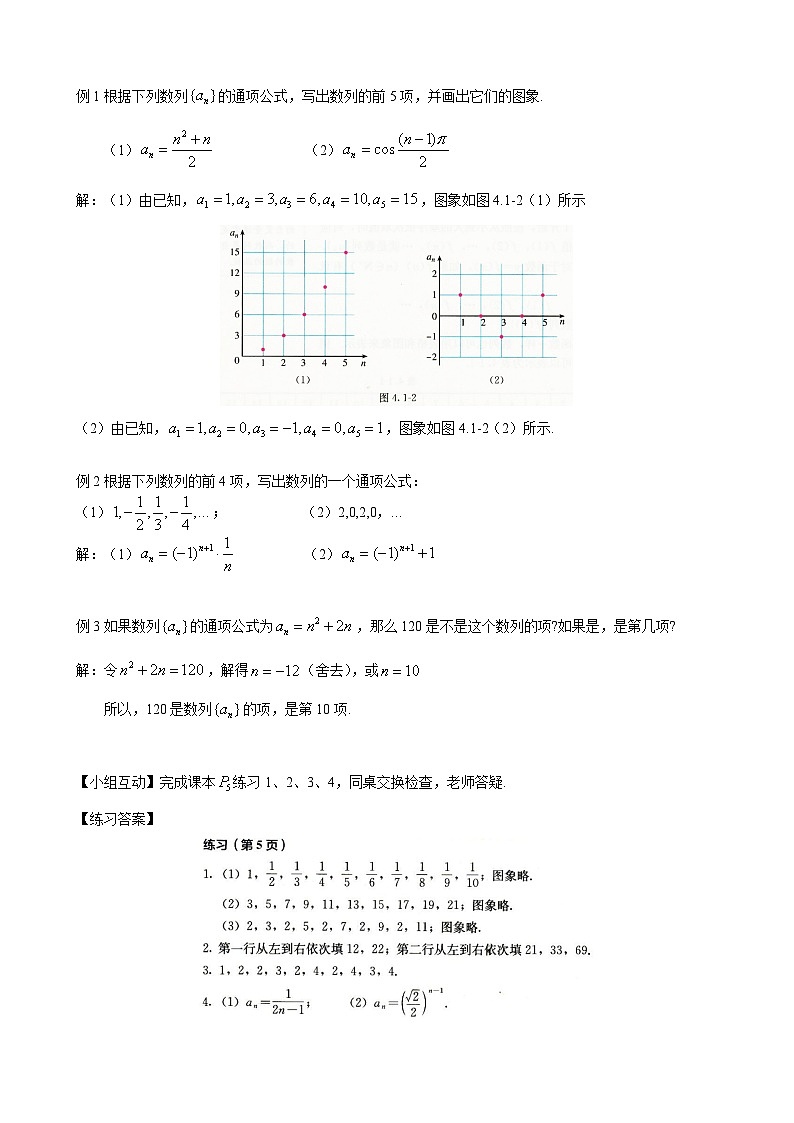
例1根据下列数列的通项公式，写出数列的前5项，并画出它们的图象.
（1） （2）
解：（1）由已知，，图象如图4.1-2（1）所示
（2）由已知，，图象如图4.1-2（2）所示.
例2根据下列数列的前 4项，写出数列的一个通项公式：
（1）； （2）2,0,2,0，…
解：（1） （2）
例3如果数列的通项公式为，那么120是不是这个数列的项?如果是，是第几项?
解：令，解得（舍去），或
所以，120是数列的项，是第10项.
【小组互动】完成课本练习1、2、3、4，同桌交换检查，老师答疑.
【练习答案】
（三）探索与发现、思考与感悟
1. 已知，则数列是( )
A.递增数列 B.递减数列 C.常数列 D.摆动数列
解：由已知，，所以，此数列为递增数列. 故选A
2.数列的通项公式为，则数列各项中最小项是( )
A.第4项B.第5项C.第6项D.第7项
解：由已知，，因为，所以时，最小，故选B
3.（多选）根据数列的前几项写出数列的一个通项公式，下列结论中正确的是（ ）
A.数列的一个通项公式为
B.数列的一个通项公式为
C.数列的一个通项公式为
D.数列的一个通项公式为.
解：对于A，数列化为，所以，正确；
对于B，利用的性质，可知，正确；
对于C，数列化为，所以，正确；
对于D，数列化为，所以. 故选ABCD
3.已知数列的通项公式为，则是此数列的第________项.
解：由已知，，可知
，所以是数列的第8项.
答案：8
4. 图中由火柴棒拼成的一列图形中,第个图形由个正方形组成：
通过观察可以发现：在第个图形中,火柴棒有________根.
解：
答案：
（四）归纳小结，回顾重点
（五）作业布置，精炼双基
1.完成课本习题4.1 1、3、7
2.预习4.2 等差数列
五、教学反思：（课后补充，教学相长）
图形
16MB
32MB
64MB
128MB
256MB
512MB
1024MB
2048MB
…
数列的概念
数列
一般地， 我们把按照确定的顺序排列的一列数称为数列 (sequence f number)
项
数列中的每一个数叫做这个数列的项，第一项称为首项
数列符号
，简记为
函数关系
，其中或者它的有限子集
数列分类
项数有限的数列叫做有穷数列，项数无限的教列叫做无穷数列.
满足的数列称为递增数列，满足的数列称为递减数列.
各项都相等的数列叫做常数列
通项公式
数列的第项与序号之间的对应关系的数学关系式.
方法一
方法二
方法一：第1个图形中,火柴棒有根，
第2个图形中,火柴棒有根，
第3个图形中,火柴棒有根，
第4个图形中,火柴棒有根，
…
第个图形中,火柴棒有根.
方法一：第1个图形中,火柴棒有根，
第2个图形中,火柴棒有根，
第3个图形中,火柴棒有根，
第4个图形中,火柴棒有根，
…
第个图形中,火柴棒有根.
数列的概念
数列
一般地， 我们把按照确定的顺序排列的一列数称为数列 (sequence f number)
项
数列中的每一个数叫做这个数列的项，第一项称为首项
数列符号
，简记为
函数关系
，其中或者它的有限子集
数列分类
项数有限的数列叫做有穷数列，项数无限的教列叫做无穷数列.
满足的数列称为递增数列，满足的数列称为递减数列.
各项都相等的数列叫做常数列
通项公式
数列的第项与序号之间的对应关系的数学关系式.