人教A版 (2019)选择性必修 第二册5.3 导数在研究函数中的应用教案设计

这是一份人教A版 (2019)选择性必修 第二册5.3 导数在研究函数中的应用教案设计，共7页。教案主要包含了教学目标，教学重点，学法与教学用具，教学过程，教学反思等内容，欢迎下载使用。

函数的最大（小）值
一、教学目标
1、探索并应用函数极值与导数的关系求函数最大（小）值.
2、掌握利用导数求取函数极值的方法.
二、教学重点、难点
重点：利用导数求函数最大（小）值.
难点：熟练应用导数解决函数最大（小）值问题.
三、学法与教学用具
1、学法：学生在老师的引导下，通过阅读教材，自主学习、思考、交流、讨论和概括，从而完成本节课的教学目标.
2、教学用具：多媒体设备等
四、教学过程
（一）创设情景，揭示课题
【回顾】
【问题】如图
是函数的极小值，是函数的极小值.
在区间上，如何求函数的最大值和最小值？
（二）阅读精要，研讨新知
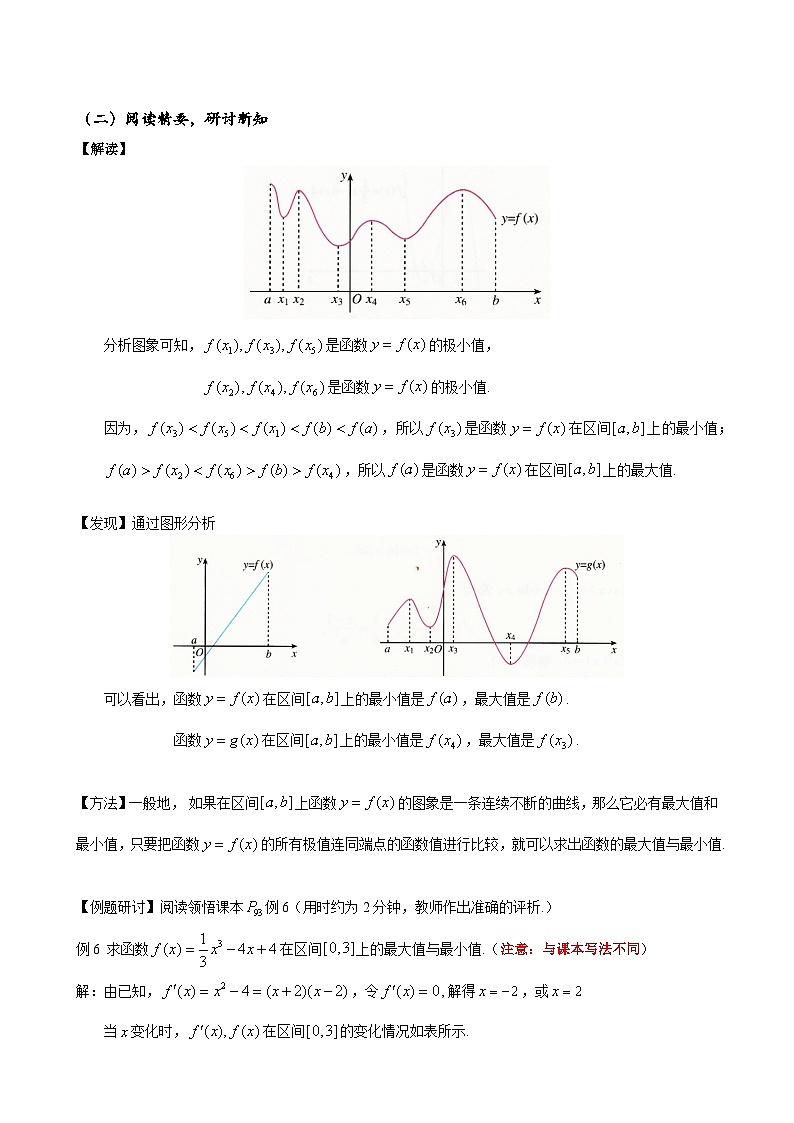
【解读】
分析图象可知，是函数的极小值，
是函数的极小值.
因为，，所以是函数在区间上的最小值；
，所以是函数在区间上的最大值.
【发现】通过图形分析
可以看出，函数在区间上的最小值是，最大值是.
函数在区间上的最小值是，最大值是.
【方法】一般地， 如果在区间上函数的图象是一条连续不断的曲线，那么它必有最大值和最小值，只要把函数的所有极值连同端点的函数值进行比较，就可以求出函数的最大值与最小值.
【例题研讨】阅读领悟课本例6（用时约为2分钟，教师作出准确的评析.）
例6 求函数在区间上的最大值与最小值.（注意：与课本写法不同）
解：由已知，，令, 解得，或
当变化时，在区间的变化情况如表所示.
所以，在区间上的最大值是，，最小值是.
【结论】一般地，求函数在区间上的最大值与最小值的步骤如下：
（1）求函数在区间上的极值；
（2）将函数的各极值与端点处的函数值比较，
其中最大的一个是最大值，最小的一个是最小值.
【问题与思考】从例4中引发的结论：
当时，证明：.
证明：由已知，得，设，则
令，解得.
当变化时，在区间的变化情况如表所示.
所以，当时，取得最小值，所以
即
所以，当时，.
【小组互动】完成课本练习1、2，同桌交换检查，老师答疑.
【练习答案】
（三）探索与发现、思考与感悟
1.（多选）已知函数,下列说法中正确的有（ ）
A. 在上有两个极值点 B.在处取得最大值
C.在处取得极小值 D.函数在上有三个不同的零点
解：由已知，
令,得或
当时, , 当时, , 当时, ,
所以函数在处取得极小值,在处取得极大值，所以A正确，B错误，C正确；
由解得或，所以D错误. 故选AC
2.已知 (是常数)在上有最大值3,那么此函数在上的最小值为( )
A. B. C. D.
解：由已知，，令,解得或.
因为,
所以，所以，最小值为,故选A.
3. 设直线与函数的图象分别交于点,则当达到最小值时的值为( )
A.1B. C. D.
解：因为的图象始终在的上方，所以
设,则，令，又,得,
所以在上单调递减,在上单调递增,
所以当时有最小值，故. 故选D.
4. 已知函数
（1）求的单调区间；
（2）设，若在上不单调且仅在处取得最大值，求的取值范围．
解：（1）由已知得
当时，有，此时在上单调递增.
当时，由得，因为，所以
由及得
此时在上单调递增，在上单调递减.
（2）由已知得，所以
设，
若在上不单调，则，即
所以
又仅在处取得最大值，
所以满足即可，即
解得
所以的取值范围为
（四）归纳小结，回顾重点
一般地，求函数在区间上的最大值与最小值的步骤如下：
（1）求函数在区间上的极值；
（2）将函数的各极值与端点处的函数值比较，
其中最大的一个是最大值，最小的一个是最小值.
（五）作业布置，精炼双基
1.完成课本习题5.3 6
2.预习5.3.2 函数的极值与最大（小）值
五、教学反思：（课后补充，教学相长）函数的极值的求取方法
解方程，当时
如果在的附近的左侧，
右侧，那么是极大值.
如果在的附近的左侧，
右侧，那么是极大值.
极小值点、极大值点统称为极值点，极小值和极大值统称为极值(extremum)
0
2
3
0
单调递减
极小值
单调递增
1
0
单调递减
极小值
单调递增