人教版（2024）六年级上册9 总复习第四课时教学设计

这是一份人教版（2024）六年级上册9 总复习第四课时教学设计，共4页。教案主要包含了知识点一，知识点二，知识点三，知识点四等内容，欢迎下载使用。

【知识点一】描述物体的位置
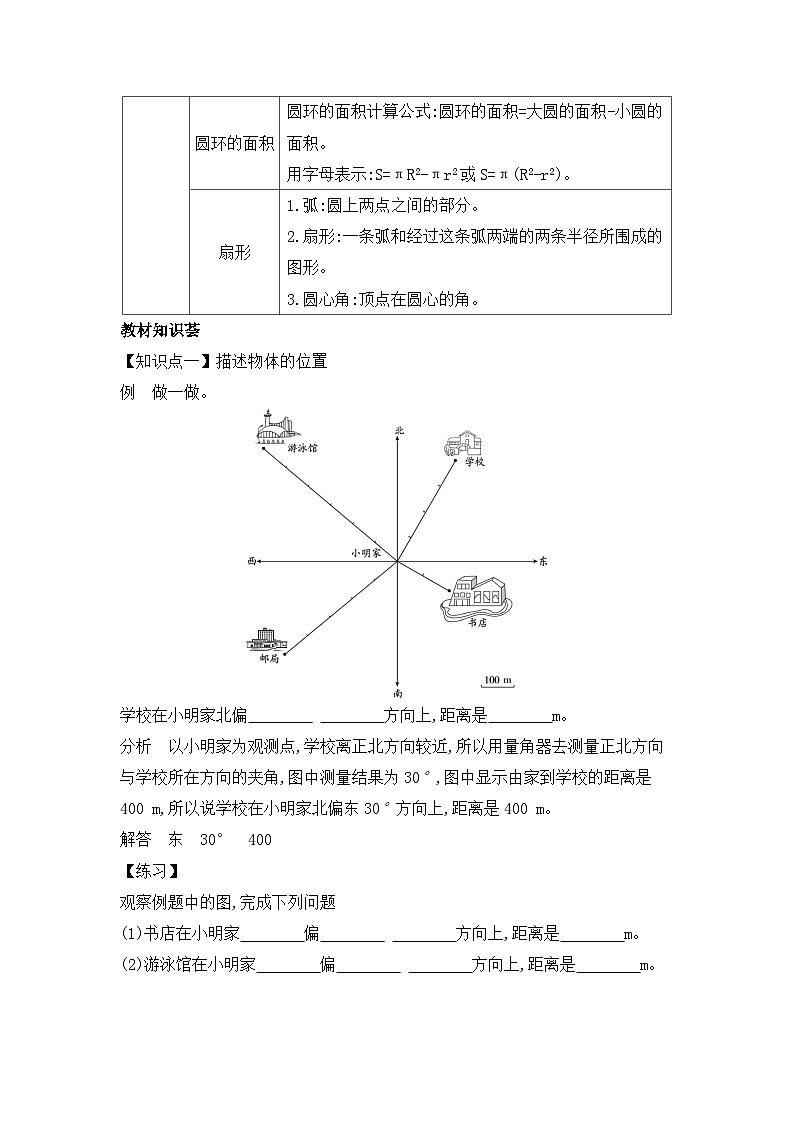
例 做一做。
学校在小明家北偏 方向上,距离是 m。
分析 以小明家为观测点,学校离正北方向较近,所以用量角器去测量正北方向与学校所在方向的夹角,图中测量结果为30°,图中显示由家到学校的距离是400 m,所以说学校在小明家北偏东30°方向上,距离是400 m。
解答 东 30° 400
【练习】
观察例题中的图,完成下列问题
(1)书店在小明家 偏 方向上,距离是 m。
(2)游泳馆在小明家 偏 方向上,距离是 m。
(3)邮局在小明家 偏 方向上,距离是 m。
答案(1)东 南 30° 200 (2)西 北 40° 600 (3)西 南 40° 500
【知识点二】圆的周长计算公式的应用
例 一个圆形花坛的直径是8 m,它的周长是多少米?
分析 已知圆的直径,直接根据“圆的周长=圆周率×直径”计算圆的周长。
解答 3.14×8=25.12(m) 答:它的周长是25.12 m。
【练习】
一个木桩的横截面是一个圆,其周长是37.68 m。它的直径是多少米?
答案 37.68÷3.14=12(m) 答:它的直径是12 m。
【知识点三】圆的面积公式的应用
例 小明家的圆形桌面的半径是0.6 m,这个桌面的面积是多少平方米?
分析 已知圆的半径,直接根据“圆的面积=圆周率×半径的平方”计算圆的面积。
解答 3.14×0.62=1.1304(m2) 答:这个桌面的面积是1.1304 m2。
【练习】
一个圆形水池的周长是18.84 m,这个水池的占地面积是多少平方米?
答案 18.84÷3.14÷2=3(m) 3.14×32=28.26(m2)
答:这个水池的占地面积是28.26 m2。
【知识点四】圆环的面积计算公式的应用
例 计算阴影部分面积(见右图)。
分析 阴影部分是一个圆环,用大圆的面积减去小圆的面积即可。
解答 3.14×122-3.14×82=3.14×144-3.14×64=251.2(cm2)
【练习】
某社区修建一个圆形花坛,半径是3 m,在花坛周围又修了一条宽是2 m的环形小路。小路的面积是多少平方米?
解答 3.14×(3+2)2-3.14×32=50.24(m2)
答:小路的面积是50.24 m2。
我的反思:
知识板块
要点梳理
具体内容
位置与方向
描述物体的位置
方向和距离,两个条件缺一不可。
在平面上标出物体位置的方法
先确定方向,再确定距离,最后画出物体的具体位置,并标示名称。
描述路线图的方法
按行走路线确定观测点,再确定行走的方向和距离。
圆
圆各部分的名称
1.圆心:圆中心的一点叫作圆心,一般用字母“O”表示。圆心可以确定圆的位置。
2.半径:连接圆心和圆上任意一点的线段叫作半径,一般用字母“r”表示。圆有无数条半径,半径确定圆的大小。
3.直径:通过圆心并且两端都在圆上的线段叫作直径,一般用字母“d”表示。圆有无数条直径。
圆的特征
1.圆具有对称性,圆是轴对称图形,圆有无数条对称轴(直径所在的直线)。
2.在同圆或等圆中,半径的长度都相等,直径的长度都相等,直径的长度等于半径的2倍。d=2r,r=。
圆的周长
1.围成圆的曲线叫作圆的周长,一般用字母“C”表示。
2.圆周率:圆的周长和它的直径的比值,用字母“π”表示。
3.圆的周长计算公式:圆的周长=圆周率×直径。
用字母表示:C=πd或C=2πr。
圆的面积
1.圆的面积:圆占平面的大小叫作圆的面积,用字母“S”表示。
2.圆的面积计算公式:圆的面积=圆周率×半径的平方。
用字母表示:S=πr2。
圆环的面积
圆环的面积计算公式:圆环的面积=大圆的面积-小圆的面积。
用字母表示:S=πR2-πr2或S=π(R2-r2)。
扇形
1.弧:圆上两点之间的部分。
2.扇形:一条弧和经过这条弧两端的两条半径所围成的图形。
3.圆心角:顶点在圆心的角。