高考数学一轮复习《考点•题型•技巧》精讲与精练高分突破专题2.4指数与指数函数(原卷版+解析)

这是一份高考数学一轮复习《考点•题型•技巧》精讲与精练高分突破专题2.4指数与指数函数(原卷版+解析)，共38页。试卷主要包含了aras＝ar＋s，s＝ars，r＝arbr，已知，，，则，已知函数，则下列叙述正确的是，已知函数，则等内容，欢迎下载使用。

知识点总结
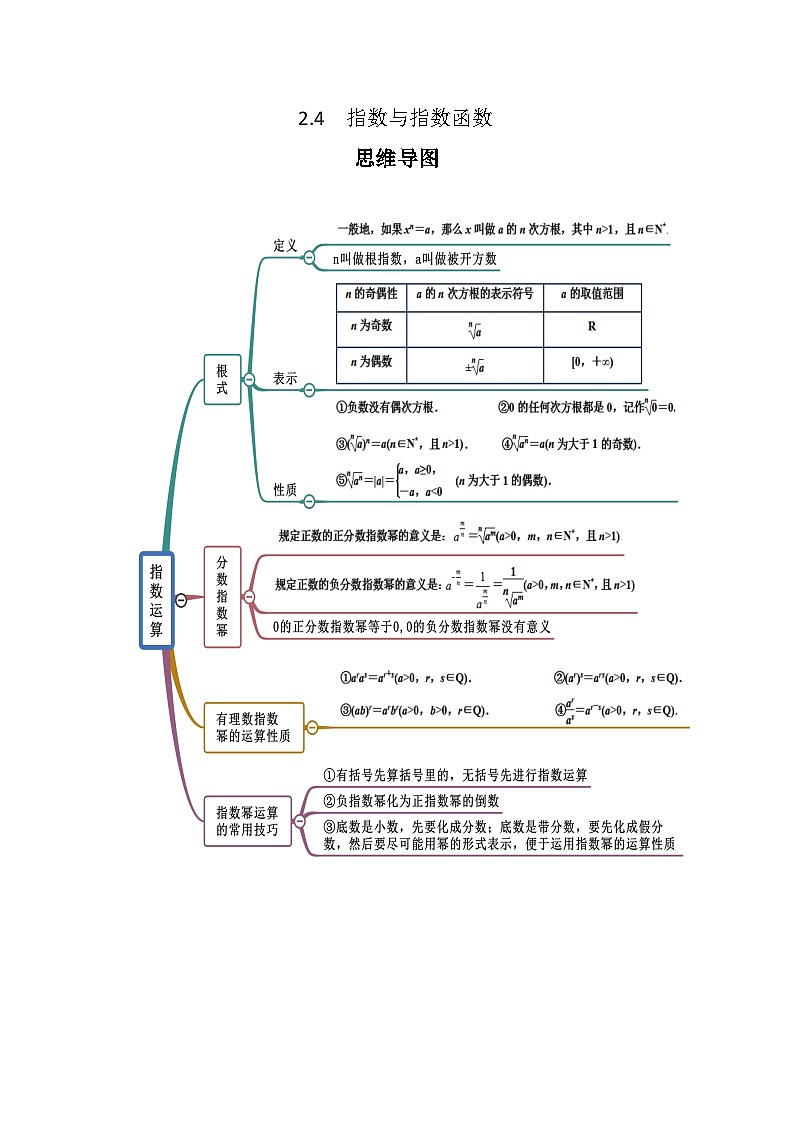
知识点一 无理数指数幂
一般地，无理数指数幂aα(a>0，α为无理数)是一个确定的 ．有理数指数幂的运算性质同样适用于无理数指数幂．
知识点二 实数指数幂的运算性质
1．aras＝ar＋s(a>0，r，s∈R)．
2．(ar)s＝ars(a>0，r，s∈R)．
3．(ab)r＝arbr(a>0，b>0，r∈R)．
知识点三 分数指数幂的意义
知识点四 有理数指数幂的运算性质
整数指数幂的运算性质，可以推广到有理数指数幂，即：
(1)aras＝ar＋s(a>0，r，s∈Q)；
(2)(ar)s＝ars(a>0，r，s∈Q)；
(3)(ab)r＝arbr(a>0，b>0，r∈Q)．
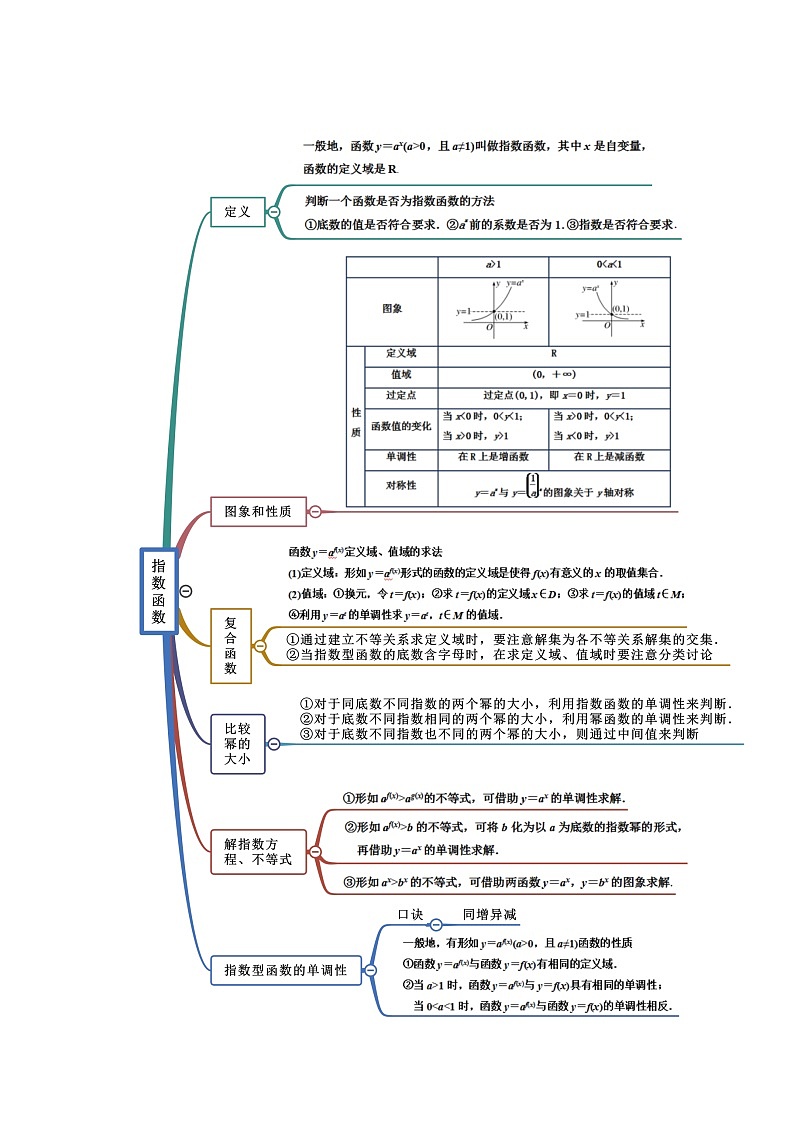
知识点四 指数函数的定义
一般地，函数 (a>0，且a≠1)叫做指数函数，其中x是自变量，函数的定义域是R.
思考 为什么底数应满足a>0且a≠1?
答案 ①当a≤0时，ax可能无意义；②当a>0时，x可以取任何实数；③当a＝1时，ax＝1 (x∈R)，无研究价值．因此规定y＝ax中a>0，且a≠1.
知识点五 两类指数模型
1．y＝kax(k>0)，当 时为指数增长型函数模型．
2．y＝kax(k>0)，当 时为指数衰减型函数模型．
知识点六 指数函数的图象和性质
指数函数y＝ax(a>0，且a≠1)的图象和性质如下表：
典型例题分析
考向一 运用指数幂运算公式化简求值
例1 计算下列各式(式中字母都是正数)：
(1)
(2)
(3)
反思感悟 一般地，进行指数幂运算时，可将系数、同类字母归在一起，分别计算；化负指数为正指数，化小数为分数进行运算，便于进行乘除、乘方、开方运算，可以达到化繁为简的目的．
考向二 分数指数幂运算的综合应用
例2 (1)已知am＝4，an＝3，求eq \r(am－2n)的值；
(2)已知＝3，求下列各式的值．
①a＋a－1；②a2＋a－2；③
反思感悟 条件求值问题的解法
(1)求解此类问题应注意分析已知条件，通过将已知条件中的式子变形(如平方、因式分解等)，寻找已知式和待求式的关系，可考虑使用整体代换法．
(2)利用整体代换法解决分数指数幂的计算问题，常常运用完全平方公式及其变形公式．
考向三 指数函数的图象及应用
例1 (1)函数y＝ax－eq \f(1,a)(a>0，且a≠1)的图象可能是( )
(2)函数f(x)＝1＋ax－2(a>0，且a≠1)恒过定点________．
(3)已知函数y＝3x的图象，怎样变换得到y＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)))x＋1＋2的图象？并画出相应图象．
反思感悟 处理函数图象问题的策略
(1)抓住特殊点：指数函数的图象过定点(0,1)，求指数型函数图象所过的定点时，只要令指数为0，求出对应的y的值，即可得函数图象所过的定点．
(2)巧用图象变换：函数图象的平移变换(左右平移、上下平移)．
(3)利用函数的性质：奇偶性与单调性．
考向四 比较大小
例4 (1)比较下列各题中两个值的大小．
①1.7－2.5,1.7－3；②1.70.3,1.50.3；③1.70.3,
(2)设 则a，b，c的大小关系为________．(用“>”连接)
反思感悟 比较幂值大小的3种类型及处理方法
基础题型训练
一、单选题
1．化简的结果为（ ）
A．B．
C．D．
2．函数，则方程的解集是（ ）
A．B．C．D．
3．已知函数g（x）=3x+t的图象不经过第二象限，则t的取值范围为
A．t≤–1B．t0，m，n∈N*，且n>1)
负分数指数幂
规定：＝eq \f(1,\r(n,am))(a>0，m，n∈N*，且n>1)
0的分数指数幂
0的正分数指数幂等于0,0的负分数指数幂无意义
a>1
00，r，s∈R)．
2．(ar)s＝ars(a>0，r，s∈R)．
3．(ab)r＝arbr(a>0，b>0，r∈R)．
知识点三 分数指数幂的意义
知识点四 有理数指数幂的运算性质
整数指数幂的运算性质，可以推广到有理数指数幂，即：
(1)aras＝ar＋s(a>0，r，s∈Q)；
(2)(ar)s＝ars(a>0，r，s∈Q)；
(3)(ab)r＝arbr(a>0，b>0，r∈Q)．
知识点四 指数函数的定义
一般地，函数y＝ax(a>0，且a≠1)叫做指数函数，其中x是自变量，函数的定义域是R.
思考 为什么底数应满足a>0且a≠1?
答案 ①当a≤0时，ax可能无意义；②当a>0时，x可以取任何实数；③当a＝1时，ax＝1 (x∈R)，无研究价值．因此规定y＝ax中a>0，且a≠1.
知识点五 两类指数模型
1．y＝kax(k>0)，当a>1时为指数增长型函数模型．
2．y＝kax(k>0)，当00，且a≠1)的图象可能是( )
答案 D
(2)函数f(x)＝1＋ax－2(a>0，且a≠1)恒过定点________．
答案 (2,2)
(3)已知函数y＝3x的图象，怎样变换得到y＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)))x＋1＋2的图象？并画出相应图象．
解 y＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)))x＋1＋2＝3－(x＋1)＋2.
作函数y＝3x关于y轴的对称图象得函数y＝3－x的图象，再向左平移1个单位长度就得到函数y＝3－(x＋1)的图象，最后再向上平移2个单位长度就得到函数y＝3－(x＋1)＋2＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3)))x＋1＋2的图象，如图所示．
反思感悟 处理函数图象问题的策略
(1)抓住特殊点：指数函数的图象过定点(0,1)，求指数型函数图象所过的定点时，只要令指数为0，求出对应的y的值，即可得函数图象所过的定点．
(2)巧用图象变换：函数图象的平移变换(左右平移、上下平移)．
(3)利用函数的性质：奇偶性与单调性．
考向四 比较大小
例4 (1)比较下列各题中两个值的大小．
①1.7－2.5,1.7－3；②1.70.3,1.50.3；③1.70.3,
考点 指数幂的大小比较
题点 比较指数幂大小
解 (1)①∵1.7>1，
∴y＝1.7x在(－∞，＋∞)上是增函数．
∵－2.5>－3，∴1.7－2.5>1.7－3.
②方法一 ∵1.70.3>0,1.50.3>0，且eq \f(1.70.3,1.50.3)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1.7,1.5)))0.3，
又eq \f(1.7,1.5)>1,0.3>0，∴eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1.7,1.5)))0.3>1，∴1.70.3>
方法二 幂函数y＝x0.3在(0，＋∞)上单调递增，
又1.7>1.5，∴1.70.3>
③∵1.70.3>1.70＝1,0.83.1
(2)设 则a，b，c的大小关系为________．(用“>”连接)
答案 c>a>b
解析 构造幂函数(x∈(0，＋∞))，由该函数在定义域内单调递增，知a>b；构造指数函数y＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))x，由该函数在定义域内单调递减，知aa>b.
反思感悟 比较幂值大小的3种类型及处理方法
基础题型训练
一、单选题
1．化简的结果为（ ）
A．B．
C．D．
【答案】B
【分析】利用平方差公式结合指数运算性质即可
【详解】因为，
，
，
，
，
所以原式=
故选：B
2．函数，则方程的解集是（ ）
A．B．C．D．
【答案】B
【分析】令，则，当时，，转化为图象的交点问题；当时，成立，进一步求出的范围，即可求出答案.
【详解】由函数，令，则，
当时，，
令，其图象如图所示
．
时，无解，
当时，成立，
由，得当时，有，解得；
当时，有，解得，
综上，的取值范围是．
故选：B.
3．已知函数g（x）=3x+t的图象不经过第二象限，则t的取值范围为
A．t≤–1B．t0，m，n∈N*，且n>1)
负分数指数幂
规定：＝eq \f(1,\r(n,am))(a>0，m，n∈N*，且n>1)
0的分数指数幂
0的正分数指数幂等于0,0的负分数指数幂无意义
a>1
01；
当x