高三数学一轮复习第二章函数第七课时函数的图象及其应用课件

这是一份高三数学一轮复习第二章函数第七课时函数的图象及其应用课件，共27页。PPT课件主要包含了－fx，f－x，－f－x，fax，afx等内容，欢迎下载使用。

考点一　作函数图象1．利用描点法作函数的图象步骤：(1)确定函数的定义域；(2)化简函数解析式；(3)讨论函数的性质(奇偶性、单调性、周期性、对称性等)；(4)列表(尤其注意特殊点、零点、最大值点、最小值点、与坐标轴的交点等)，描点，连线．
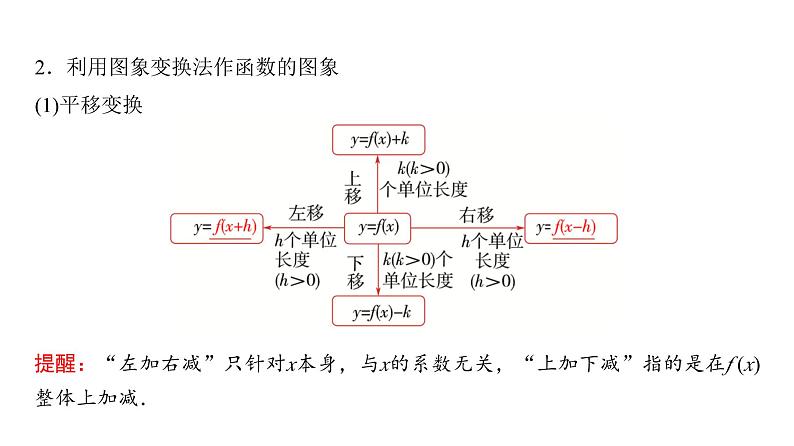
2．利用图象变换法作函数的图象(1)平移变换
提醒：“左加右减”只针对x本身，与x的系数无关，“上加下减”指的是在f (x)整体上加减．
lg a x(a＞0且a≠1)
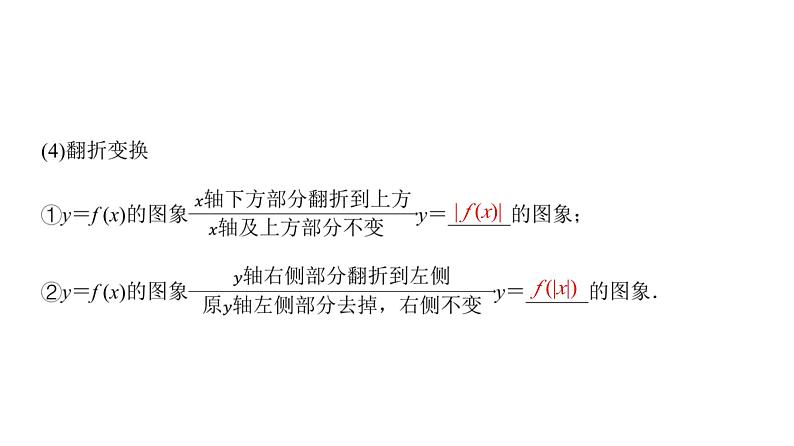
跟进训练1　作出下列函数的图象．(1)y＝10|lg x| ；(2)y＝|lg2x－1|．
考点二　函数图象的辨识辨析函数图象的入手点，具体如下：
A　　　　　　 　　　　　B
C　　　　　　 　　　　　D
链接·2024高考试题(2024·全国甲卷数学(理)真题)函数f (x)＝－x2＋(ex－e－x)sin x在区间[－2.8，2.8]的大致图象为(　　)
A　　　　　　　 B
C　　　　　　 　 D
A　　　　　 　　 B
C　　　　　 　 　 D
A　　　　　 　 B
C　　　　　 　 D
(2)画出函数f (x)的图象如图所示．不妨令a＜b＜c，则1－2a＝2b－1，则2a＋2b＝2．结合图象可得4＜c＜5，故16＜2c＜32，所以18＜2a＋2b＋2c＜34．]
点拨　解决本例(1)需熟知对于已知解析式或易画出在给定区间上的图象的函数，常借助图象研究其性质：(1)从图象的最高点、最低点分析函数的最值、极值．(2)从图象的对称性分析函数的奇偶性．(3)从图象的走向趋势分析函数的单调性、周期性．本例(2)解决的关键是转化为函数图象的交点问题，结合图象即可．