高三数学一轮复习第三章一元函数的导数及其应用第一课时导数的概念、几何意义及运算学案

这是一份高三数学一轮复习第三章一元函数的导数及其应用第一课时导数的概念、几何意义及运算学案，共18页。学案主要包含了教师备选资源，教师备用等内容，欢迎下载使用。
【教师备选资源】
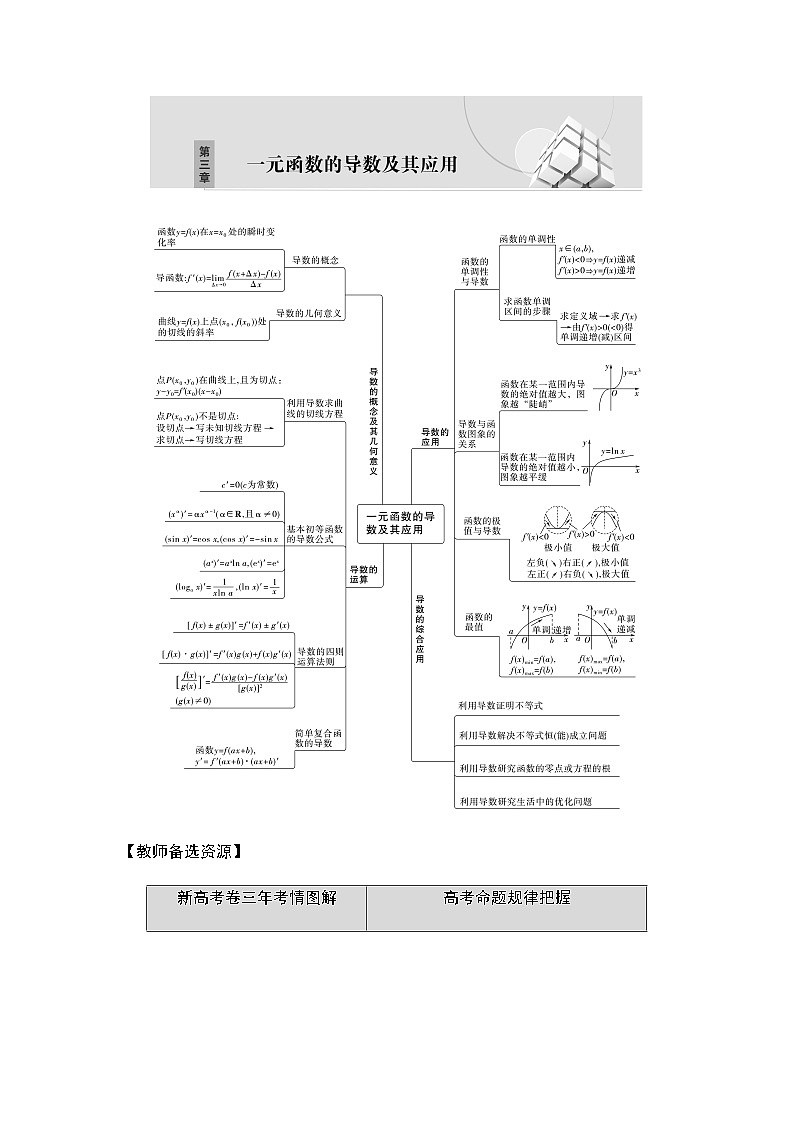
第1课时 导数的概念、几何意义及运算
[考试要求] 1．了解导数的概念，掌握基本初等函数的导数．2．通过函数图象，理解导数的几何意义．3．能够用导数公式和导数的运算法则求简单函数的导数，能求简单的复合函数(形如f (ax＋b))的导数．
考点一 导数的概念
1．导数的概念
函数f (x)在x＝x0处瞬时变化率是limΔx→0ΔyΔx＝limΔx→0fx0+Δx-fx0Δx，我们称它为函数y＝f (x)在x＝x0处的导数，记作f ′(x0)或y'|x＝x0．
2．导数概念的诠释
(1)增量Δx可以是正数，也可以是负数，但是不可以等于0．Δx→0的意义：Δx与0之间距离要多近有多近，即|Δx→0|可以小于给定的任意小的正数；
(2)当Δx→0时，Δy在变化中都趋于0，但它们的比值却趋于一个确定的常数，即存在一个常数与ΔyΔx＝fx0+Δx-fx0Δx无限接近；
(3)导数的本质就是函数的平均变化率在某点处的极限，即瞬时变化率．如瞬时速度即是位移在这一时刻的瞬间变化率，即f ′(x0)＝limΔx→0ΔyΔx＝limΔx→0fx0+Δx-fx0Δx．
[典例1] (2024·长春吉大附中模拟预测)利用导数的定义计算limΔx→0lne+2Δx-lneΔx值为( )
A．1 B．2e
C．0 D．2
B [依题意，令函数f (x)＝ln x，求导得f ′(x)＝1x，所以limΔx→0lne+2Δx-lneΔx
＝2limΔx→0fe+2Δx-fe2Δx＝2f ′(e)＝2e．故选B．]
在本例中，解题的关键是熟知导数定义的内涵．
跟进训练1 设函数f (x)在点(1，f (1))处的切线方程为y＝2x＋1，则limΔx→0f1+Δx-f12Δx＝( )
A．4 B．2
C．1 D．12
C [∵函数f (x)在点(1，f (1))处的切线方程为y＝2x＋1，∴f ′(1)＝2，
则limΔx→0f1+Δx-f12Δx
＝12limΔx→0f1+Δx-f1Δx＝12f ′(1)
＝1．
故选C．]
考点二 导数的运算法则
1．基本初等函数的导数
2．导数的四则运算法则
若f ′(x), g′(x)存在，则
(1)[f (x)±g(x)]′＝f ′(x)±g′(x)；
(2)[f (x)g(x)]′＝f ′(x)g(x)＋f (x)g′(x)；
(3)fxgx′＝f'xgx-fxg'xgx2(g(x)≠0)；
(4)[cf (x)]′＝cf ′(x)(c为常数)．
3．复合函数的导数
复合函数y＝f (g(x))的导数和函数y＝f (u)，u＝g(x)的导数间的关系为y′x＝y′u·u′x，即y对x的导数等于y对u的导数与u对x的导数的乘积．
[典例2] 求下列函数的导函数：
(1)y＝x4－3x2－5x＋6；
(2)y＝2x＋sin x2cs x2；
(3)y＝csxx；
(4)y＝ln (2x－3)＋xe－x．
[解] (1)因为y＝x4－3x2－5x＋6，所以y′＝4x3－6x－5．
(2)因为y＝2x＋sin x2cs x2＝2x＋12sin x，
所以y′＝2x ln 2＋12cs x．
(3)因为y＝csxx，所以y′＝-sinx·x-csx·1x2＝－x·sinx+csxx2．
(4)因为y＝ln (2x－3)＋xe－x，所以y′＝[ln (2x－3)]′＋(xe－x)′＝22x-3＋e－x－xe－x．
本例中，解题的关键是掌握求导公式及其运算法则．
跟进训练2 已知f (x)＝cs 2x＋e2x，则f ′(x)＝( )
A．－2sin 2x＋2e2x B．sin 2x＋e2x
C．2sin 2x＋2e2x D．－sin 2x＋e2x
A [f ′(x)＝－2sin 2x＋2e2x，故选A．]
考点三 导数的几何意义
f ′(x0)是曲线y＝f (x)在点(x0，f (x0))处的切线的斜率，从而在点(x0, f (x0))处的切线方程为y－f (x0)＝f ′(x0)·(x－x0)．
[典例3] (1)已知函数f (x)＝ln (x＋1)，则f (1)，f22，f33的大小关系为( )
A．f (1)