高三数学一轮复习第七章立体几何与空间向量第三课时空间直线、平面的平行课件

这是一份高三数学一轮复习第七章立体几何与空间向量第三课时空间直线、平面的平行课件，共32页。PPT课件主要包含了平面外，此平面内，相交直线等内容，欢迎下载使用。

考点一　与线、面平行相关命题的判定1．如果一个平面内的两条____直线分别平行于另一个平面内的两条____直线，则这两个平面平行. 2．平行于同一个平面的两个平面____. 3．垂直于同一条直线的两个平面____. 4．如果两个平面平行，那么其中一个平面内的直线平行于另一个平面. 5．如果一条直线垂直于两个平行平面中的一个平面，那么它也垂直于另一个平面.
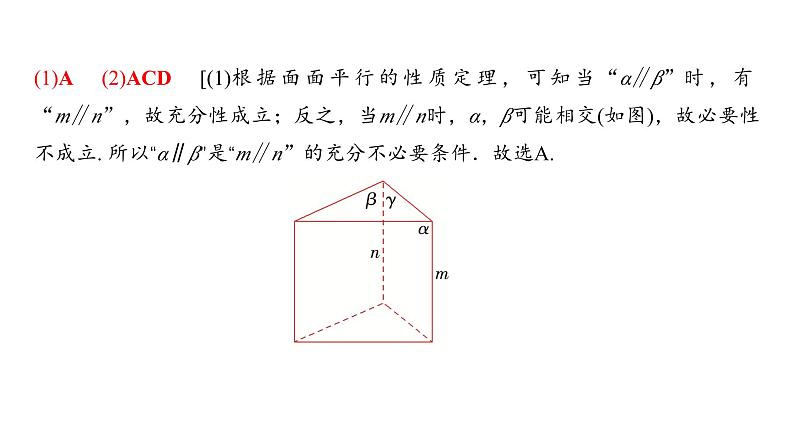
[典例1]　(1)(2024·贵州期末)已知三个不同的平面α，β，γ和直线m，n，若α∩γ＝m，β∩γ＝n，则“α∥β”是“m∥n”的(　　)A．充分不必要条件　B．必要不充分条件C．充要条件　D．既不充分也不必要条件
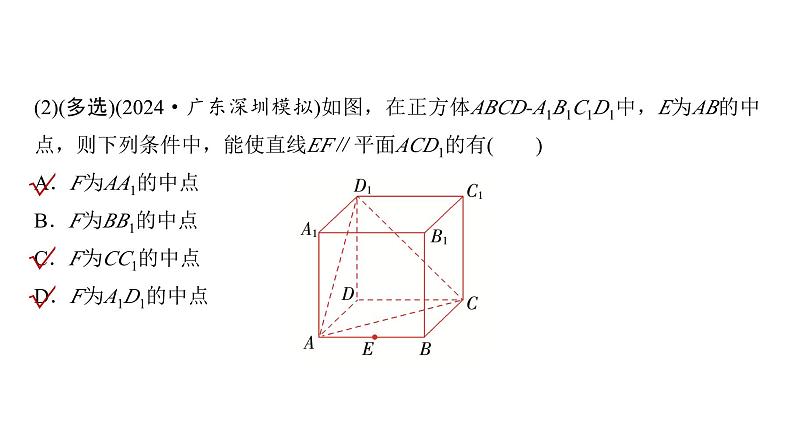
(2)(多选)(2024·广东深圳模拟)如图，在正方体ABCD-A1B1C1D1中，E为AB的中点，则下列条件中，能使直线EF∥平面ACD1的有(　　)A．F为AA1的中点B．F为BB1的中点　C．F为CC1的中点　D．F为A1D1的中点
(1)A　(2)ACD　[(1)根据面面平行的性质定理，可知当“α∥β”时，有“m∥n”，故充分性成立；反之，当m∥n时，α，β可能相交(如图)，故必要性不成立. 所以“α∥β”是“m∥n”的充分不必要条件．故选A.
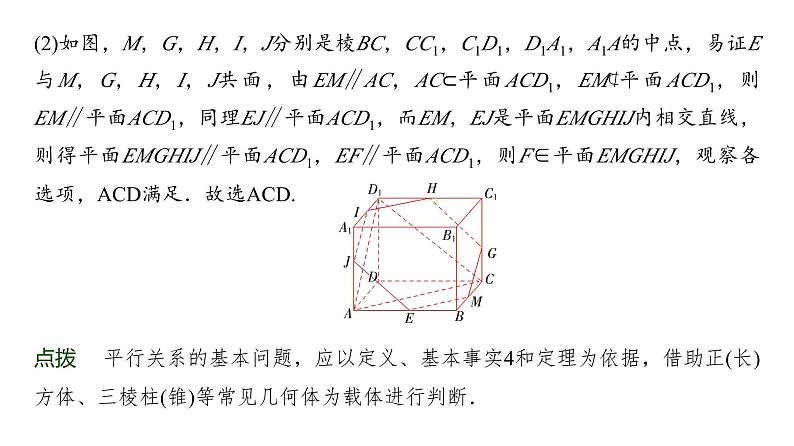
(2)如图，M，G，H，I，J分别是棱BC，CC1，C1D1，D1A1，A1A的中点，易证E与M，G，H，I，J共面，由EM∥AC，AC⊂平面ACD1，EM⊄平面ACD1，则EM∥平面ACD1，同理EJ∥平面ACD1，而EM，EJ是平面EMGHIJ内相交直线，则得平面EMGHIJ∥平面ACD1，EF∥平面ACD1，则F∈平面EMGHIJ，观察各选项，ACD满足．故选ACD.
点拨　 平行关系的基本问题，应以定义、基本事实4和定理为依据，借助正(长)方体、三棱柱(锥)等常见几何体为载体进行判断．
跟进训练1　(多选)(2024·厦门外国语学校月考)已知m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题中正确的是(　　)A．若m∥α，m∥β，则α∥βB．若m∥α，n∥α，则m∥nC．若m⊥α，n⊥α，则m∥nD．若α⊥γ，α⊥β，则γ与β可能平行，也可能相交
CD　[对于A，若α∩β＝n，m∥n，m⊄α，m⊄β，则m∥α，m∥β，所以A错误．对于B，若m∥α，n∥α，则m与n可能是异面直线，相交直线或平行直线，所以B错误．对于C，若m⊥α，n⊥α，由线面垂直的性质定理知m∥n，C正确．对于D，若α⊥γ，α⊥β，则γ与β可能相交或平行，D正确．]
考点二　直线与平面平行的判定定理与性质定理
考向1　直线与平面平行的判定[典例2]　如图，P是平行四边形ABCD所在平面外的一点，E，F分别为AB，PD的中点，求证：AF∥平面PCE.
法二(应用面面平行的判定定理及性质)：如图，设G为CD的中点，连接FG，AG.∵F，G分别为PD，CD的中点，∴FG∥PC.又E为AB的中点，AB綉CD，∴AE綉CG，∴四边形AECG是平行四边形，∴AG∥EC，又FG⊄平面PCE，AG⊄平面PCE.PC⊂平面PCE，EC⊂平面PCE，∴FG∥平面PCE，AG∥平面PCE.又FG，AG⊂平面AFG，FG∩AG＝G，∴平面AFG∥平面PCE.又AF⊂平面AFG，∴AF∥平面PCE.
考向2　线面平行性质定理的应用[典例3]　(2024·福建泉州一中月考)如图，在直四棱柱ABCD-A1B1C1D1中，E为线段AD上的任意一点(不包括A，D两点)，平面CEC1∩平面BB1D＝FG.证明：FG∥平面AA1B1B.
[证明]　在直四棱柱ABCD-A1B1C1D1中，BB1∥CC1，BB1⊂平面BB1D，CC1⊄平面BB1D，所以CC1∥平面BB1D.又CC1⊂平面CEC1，平面CEC1∩平面BB1D＝FG，所以CC1∥FG.因为BB1∥CC1，所以BB1∥FG.而BB1⊂平面AA1B1B，FG⊄平面AA1B1B，所以FG∥平面AA1B1B.
点拨　(1)应用线面平行的判定定理的关键是找到平面内与已知直线平行的直线．常利用三角形的中位线、平行四边形的对边、成比例线段出现平行线或过已知直线作一平面找其交线．(2)应用线面平行的性质定理的关键是确定交线的位置，有时需要经过已知直线作辅助平面确定交线．
跟进训练2　(2024·大同模拟)如图所示，已知四边形ABCD是正方形，四边形ACEF是矩形，M是线段EF的中点．(1)求证：AM∥平面BDE；(2)若平面ADM∩平面BDE＝l，平面ABM∩平面BDE＝m，试分析l与m的位置关系，并证明你的结论．
[解]　(1)证明：如图，记AC与BD的交点为O，连接OE.因为O，M分别为AC，EF的中点，四边形ACEF是矩形，所以四边形AOEM是平行四边形，所以AM∥OE.又因为OE⊂平面BDE，AM⊄平面BDE，所以AM∥平面BDE.
(2)l∥m，证明如下：由(1)知AM∥平面BDE，又AM⊂平面ADM，平面ADM∩平面BDE＝l，所以l∥AM，同理，AM∥平面BDE，又AM⊂平面ABM，平面ABM∩平面BDE＝m，所以m∥AM，所以l∥m.
考点三　平面与平面平行的判定与性质
[典例4]　(2024·沈阳模拟)如图所示，在三棱柱ABC-A1B1C1中，过BC的平面与上底面A1B1C1交于GH(GH与B1C1不重合)．(1)求证：BC∥GH；(2)若E，F，G分别是AB，AC，A1B1的中点，求证：平面EFA1∥平面BCHG.
[证明]　(1)∵在三棱柱ABC-A1B1C1中，平面ABC∥平面A1B1C1，又∵平面BCHG∩平面ABC＝BC，且平面BCHG∩平面A1B1C1＝HG，∴由面面平行的性质定理得BC∥GH.
(2)∵E，F分别为AB，AC的中点，∴EF∥BC，∵EF⊄平面BCHG，BC⊂平面BCHG，∴EF∥平面BCHG.又G，E分别为A1B1，AB的中点，A1B1綉AB，∴A1G綉EB，∴四边形A1EBG是平行四边形，∴A1E∥GB.∵A1E⊄平面BCHG，GB⊂平面BCHG，∴A1E∥平面BCHG.又∵A1E∩EF＝E，A1E，EF⊂平面EFA1，∴平面EFA1∥平面BCHG.
点拨　利用面面平行的判定定理证明两平面平行时需要说明是一个平面内的两条相交直线与另一个平面平行.
跟进训练3　(2024·张家口模拟)如图，四棱柱ABCD-A1B1C1D1的底面ABCD是正方形．(1)证明：平面A1BD∥平面CD1B1；(2)若平面ABCD∩平面B1D1C＝l，证明：B1D1∥l.
[证明]　(1)由题设知BB1綉DD1，所以四边形BB1D1D是平行四边形，所以BD∥B1D1.又BD⊄平面CD1B1，B1D1⊂平面CD1B1，所以BD∥平面CD1B1.因为A1D1綉B1C1綉BC，所以四边形A1BCD1是平行四边形，所以A1B∥D1C.又A1B⊄平面CD1B1，D1C⊂平面CD1B1，所以A1B∥平面CD1B1.又因为BD∩A1B＝B，BD，A1B⊂平面A1BD，所以平面A1BD∥平面CD1B1.
(2)由(1)知平面A1BD∥平面CD1B1，又平面ABCD∩平面B1D1C＝l，平面ABCD∩平面A1BD＝BD，所以l∥BD，在四棱柱ABCD-A1B1C1D1中，四边形BDD1B1为平行四边形，所以B1D1∥BD，所以B1D1∥l.
点拨　熟练掌握线线、线面、面面平行关系间的相互转化是解决线线、线面、面面平行的综合问题的关键．
[解]　(1)证明：∵在四棱锥P-ABCD中，底面ABCD是平行四边形，M，N，Q分别为BC，PA，PB的中点，∴NQ∥CD，MQ∥PC.∵NQ∩MQ＝Q，CD∩PC＝C，且NQ，MQ⊂平面MNQ，CD，PC⊂平面PCD，∴平面MNQ∥平面PCD.