高三数学一轮复习第八章解析几何第二课时两条直线的位置关系课件

这是一份高三数学一轮复习第八章解析几何第二课时两条直线的位置关系课件，共23页。PPT课件主要包含了k1·k2＝－1，k1≠k2，x＋3y－1＝0，－x－y，2a－xy，x2b－y，－y－x，y－bx＋b，b－yb－x，x＋4y－4＝0等内容，欢迎下载使用。

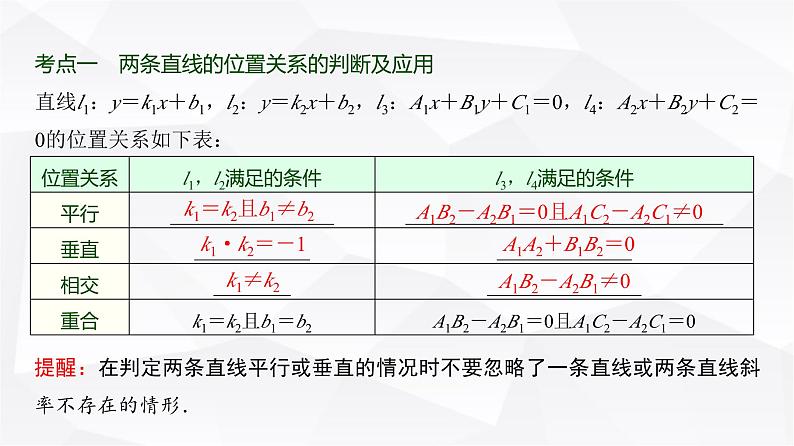
考点一　两条直线的位置关系的判断及应用直线l1：y＝k1x＋b1，l2：y＝k2x＋b2，l3：A1x＋B1y＋C1＝0，l4：A2x＋B2y＋C2＝0的位置关系如下表：
提醒：在判定两条直线平行或垂直的情况时不要忽略了一条直线或两条直线斜率不存在的情形．
k1＝k2且b1≠b2
A1B2－A2B1＝0且A1C2－A2C1≠0
A1A2＋B1B2＝0
A1B2－A2B1≠0
[常用结论]三种直线系方程(1)与直线Ax＋By＋C＝0平行的直线系方程是Ax＋By＋m＝0(m∈R且m≠C)．(2)与直线Ax＋By＋C＝0垂直的直线系方程是Bx－Ay＋n＝0(n∈R)．(3)过直线l1：A1x＋B1y＋C1＝0与l2：A2x＋B2y＋C2＝0的交点的直线系方程为A1x＋B1y＋C1＋λ(A2x＋B2y＋C2)＝0(λ∈R)，但不包括l2．
(1)A　(2)C　(3)BD　[(1)由题意可知l1⊥l2，故2a＋a(a－1)＝0，解得a＝0或a＝－1，经验证，符合题意．(2)若“直线l1：ax＋y＋2＝0与l2：x＋ay－3－a＝0平行”，则a2－1＝0，解得a＝1或a＝－1，当a＝1时，直线l1：x＋y＋2＝0，l2：x＋y－4＝0，此时l1∥l2，符合题意；当a＝－1时，直线l1：－x＋y＋2＝0，即l1：x－y－2＝0，l2：x－y－2＝0，此时l1，l2重合，不符合题意；综上所述：“直线l1：ax＋y＋2＝0与l2：x＋ay－3－a＝0平行”等价于a＝1.所以“a＝1”是“直线l1：ax＋y＋2＝0与l2：x＋ay－3－a＝0平行”的充要条件．故选C.
点拨　解决两直线平行与垂直的参数问题要“前思后想”
x＋3y－5＝0或x＝－1
点拨　1．求过两直线交点的直线方程的方法求过两直线交点的直线方程，先解方程组求出两直线的交点坐标，再结合其他条件写出直线方程，也可借助直线系方程，利用待定系数法求出直线方程．2．点到直线、两平行线间的距离公式的使用条件(1)求点到直线的距离时，应先化直线方程为一般式．(2)求两平行线之间的距离时，应先将方程化为一般式且x，y的系数对应相等．
考点三　对称问题1．点(x，y)关于原点(0，0)的对称点为___________，点(x，y)关于点(a，b)的对称点为________________．2．点(x，y)关于直线x＝a的对称点为_________，关于直线y＝b的对称点为___________．3．点(x，y)关于直线y＝x的对称点为_______，关于直线y＝－x的对称点为___________．4．点(x，y)关于直线y＝x＋b的对称点为_____________，关于直线y＝－x＋b的对称点为_____________．
(2a－x，2b－y)
考向1　中心对称问题[典例3] 　过点P(0，1)作直线l，使它被直线l1：2x＋y－8＝0和l2：x－3y＋10＝0截得的线段被点P平分，则直线l的方程为_____________．
x＋4y－4＝0　[设l1与l的交点为A(a，8－2a)，则由题意知，点A关于点P的对称点B(－a，2a－6)在l2上，代入l2的方程得－a－3(2a－6)＋10＝0，解得a＝4，即点A(4，0)在直线l上，所以直线l的方程为x＋4y－4＝0.]
考向2　轴对称问题[典例4] 　(1)已知直线y＝2x是△ABC中∠C的平分线所在的直线，若点A，B的坐标分别是(－4，2)，(3，1)，则点C的坐标为(　　)A．(－2，4) B．(－2，－4)C．(2，4) D．(2，－4)(2)已知入射光线经过点M(－3，4)，被直线l：x－y＋3＝0反射，反射光线经过点N(2，6)，则反射光线所在直线的方程为______________．
点拨　对称问题的求解策略