
2023年山东省菏泽市中考数学试卷
展开1.(3分)剪纸文化是我国最古老的民间艺术之一.下列剪纸图案中既是轴对称图形又是中心对称图形的是
A.B.
C.D.
2.(3分)下列运算正确的是
A.B.C.D.
3.(3分)一把直尺和一个含角的直角三角板按如图方式放置,若,则
A.B.C.D.
4.(3分)实数,,在数轴上对应点的位置如图所示,下列式子正确的是
A.B.C.D.
5.(3分)如图所示的几何体是由5个大小相同的小正方体组成的,它的主视图是
A.B.
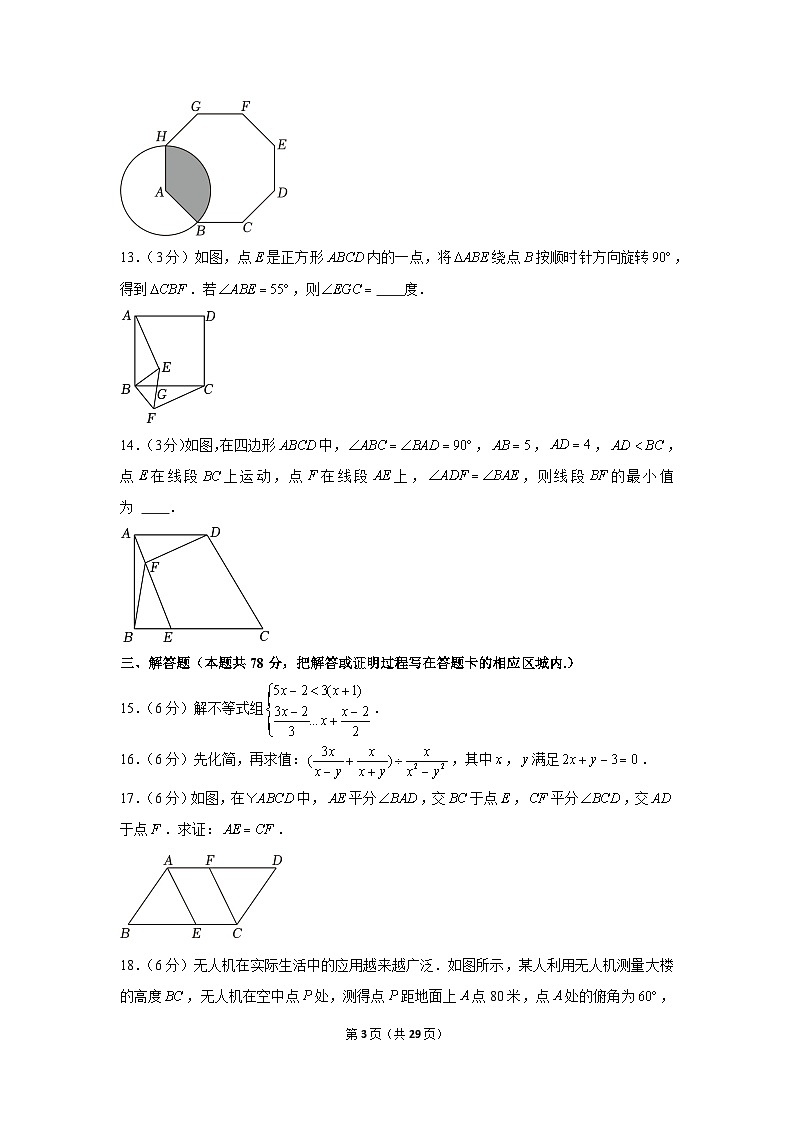
C.D.
6.(3分)一元二次方程的两根为,,则的值为
A.B.C.3D.
7.(3分)的三边长,,满足,则是
A.等腰三角形B.直角三角形
C.锐角三角形D.等腰直角三角形
8.(3分)若一个点的纵坐标是横坐标的3倍,则称这个点为“三倍点”,如:,,等都是“三倍点”.在的范围内,若二次函数的图象上至少存在一个“三倍点”,则的取值范围是
A.B.C.D.
二、填空题(本大题共6个小题,每小题3分,共18分,只要求把最后结果填写在答题卡的相应区域内.)
9.(3分)因式分解: .
10.(3分)计算: .
11.(3分)用数字0,1,2,3组成个位数字与十位数字不同的两位数,其中是偶数的概率为 .
12.(3分)如图,正八边形的边长为4,以顶点为圆心,的长为半径画圆,则阴影部分的面积为 (结果保留.
13.(3分)如图,点是正方形内的一点,将绕点按顺时针方向旋转,得到.若,则 度.
14.(3分)如图,在四边形中,,,,,点在线段上运动,点在线段上,,则线段的最小值为 .
三、解答题(本题共78分,把解答或证明过程写在答题卡的相应区城内.)
15.(6分)解不等式组.
16.(6分)先化简,再求值:,其中,满足.
17.(6分)如图,在中,平分,交于点,平分,交于点.求证:.
18.(6分)无人机在实际生活中的应用越来越广泛.如图所示,某人利用无人机测量大楼的高度,无人机在空中点处,测得点距地面上点80米,点处的俯角为,楼顶点处的俯角为,已知点与大楼的距离为70米(点,,,在同一平面内),求大楼的高度(结果保留根号).
19.(7分)某班学生以跨学科主题学习为载体,综合运用体育、数学、生物学等知识,研究体育课的运动负荷.在体育课基本部分运动后,测量统计了部分学生的心率情况,按心率次数(次分钟),分为如下五组:组:,组:,组,组:,组:.其中组数据为:73,65,74,68,74,70,66,56.
根据统计数据绘制了不完整的统计图(如图所示),请结合统计图解答下列问题:
(1)组数据的中位数是 ,众数是 ;在统计图中组所对应的扇形圆心角是 度;
(2)补全学生心率频数分布直方图;
(3)一般运动的适宜心率为(次分钟),学校共有2300名学生,请你依据此次跨学科研究结果,估计大约有多少名学生达到适宜心率?
20.(7分)如图,已知坐标轴上两点,,连接,过点作,交反比例函数在第一象限的图象于点.
(1)求反比例函数和直线的表达式;
(2)将直线向上平移个单位,得到直线,求直线与反比例函数图象的交点坐标.
21.(10分)某学校为美化学校环境,打造绿色校园,决定用篱笆围成一个一面靠墙(墙足够长)的矩形花园,用一道篱笆把花园分为,两块(如图所示),花园里种满牡丹和芍药.学校已定购篱笆120米.
(1)设计一个使花园面积最大的方案,并求出其最大面积;
(2)在花园面积最大的条件下,,两块内分别种植牡丹和芍药,每平方米种植2株,已知牡丹每株售价25元,芍药每株售价15元,学校计划购买费用不超过5万元,求最多可以购买多少株牡丹?
22.(10分)如图,为的直径,是圆上一点,是的中点,弦,垂足为点.
(1)求证:;
(2)是上一点,,,求;
(3)在(2)的条件下,当是的平分线时,求的长.
23.(10分)(1)如图1,在矩形中,点,分别在边,上,,垂足为点.求证:.
【问题解决】
(2)如图2,在正方形中,点,分别在边,上,,延长到点,使,连接.求证:.
【类比迁移】
(3)如图3,在菱形中,点,分别在边,上,,,,求的长.
24.(10分)已知抛物线与轴交于,两点,与轴交于点,其对称轴为.
(1)求抛物线的表达式;
(2)如图1,点是线段上的一动点,连接,,将沿直线翻折,得到△,当点恰好落在抛物线的对称轴上时,求点的坐标;
(3)如图2,动点在直线上方的抛物线上,过点作直线的垂线,分别交直线,线段于点,,过点作轴,垂足为,求的最大值.
2023年山东省菏泽市中考数学试卷
参考答案与试题解析
一、选择题(本大题共8个小题,每小题3分,共24分,在每小题给出的四个选项中,只有一个选项是正确的,请把正确选项的序号涂在答题卡的相应位置.
1.(3分)剪纸文化是我国最古老的民间艺术之一.下列剪纸图案中既是轴对称图形又是中心对称图形的是
A.B.
C.D.
【分析】根据轴对称图形与中心对称图形的概念求解.
【解答】解:.原图既是轴对称图形,又是中心对称图形,故此选项符合题意;
.原图是轴对称图形,不是中心对称图形,故此选项不合题意;
.原图既不是轴对称图形,也不是中心对称图形,故此选项不合题意;
.原图是中心对称图形,不是轴对称图形,故此选项不合题意.
故选:.
2.(3分)下列运算正确的是
A.B.C.D.
【分析】根据同底数幂的乘除法法则、积的乘方法则以及完全平方公式分别判断即可.
【解答】解:、原式,故本选项计算错误,不符合题意;
、原式,故本选项计算正确,符合题意;
、原式,故本选项计算错误,不符合题意;
、原式,故本选项计算错误,不符合题意;
故选:.
3.(3分)一把直尺和一个含角的直角三角板按如图方式放置,若,则
A.B.C.D.
【分析】由平行线的性质可得,从而可求.
【解答】解:如图,
由题意得:,
,,
,
.
故选:.
4.(3分)实数,,在数轴上对应点的位置如图所示,下列式子正确的是
A.B.C.D.
【分析】由数轴可得,然后得出,,,与0的大小关系,再根据有理数乘法法则进行判断即可.
【解答】解:由数轴可得,
则,,,,
那么,,,,
则,,均不符合题意,符合题意,
故选:.
5.(3分)如图所示的几何体是由5个大小相同的小正方体组成的,它的主视图是
A.B.
C.D.
【分析】根据主视图是从物体正面看所得到的图形解答即可.
【解答】解:从正面看有三列,从左到右小正方形的个数分别为2、1、1.
故选:.
6.(3分)一元二次方程的两根为,,则的值为
A.B.C.3D.
【分析】直接根据根与系数的关系得出、的值,再代入计算即可.
【解答】解:一元二次方程的两根为,,
;.
.
故选:.
7.(3分)的三边长,,满足,则是
A.等腰三角形B.直角三角形
C.锐角三角形D.等腰直角三角形
【分析】由等式可分别得到关于、、的等式,从而分别计算得到、、的值,再由 的关系,可推导得到为直角三角形.
【解答】解:由题意得,
解得,
,且,
为等腰直角三角形,
故选:.
8.(3分)若一个点的纵坐标是横坐标的3倍,则称这个点为“三倍点”,如:,,等都是“三倍点”.在的范围内,若二次函数的图象上至少存在一个“三倍点”,则的取值范围是
A.B.C.D.
【分析】由题意得,三倍点所在的直线为,根据二次函数的图象上至少存在一个“三倍点”转化为和至少有一个交点,求△,再根据和时两个函数值大小即可求出.
【解答】解:由题意得,三倍点所在的直线为,
在的范围内,二次函数的图象上至少存在一个“三倍点”,
即在的范围内,二次函数和至少有一个交点,
令,整理得,,
则△,解得,
把代入得,代入得,
,解得;
把代入得,代入得,
,解得,
综上,的取值范围为:.
故选:.
二、填空题(本大题共6个小题,每小题3分,共18分,只要求把最后结果填写在答题卡的相应区域内.)
9.(3分)因式分解: .
【分析】原式提取,再利用平方差公式分解即可.
【解答】解:原式,
故答案为:
10.(3分)计算: 1 .
【分析】首先计算零指数幂、特殊角的三角函数值和绝对值,然后计算乘法,最后从左向右依次计算,求出算式的值即可.
【解答】解:
.
故答案为:1.
11.(3分)用数字0,1,2,3组成个位数字与十位数字不同的两位数,其中是偶数的概率为 .
【分析】画树状图,共有9种等可能的结果,其中是偶数的结果有5种,再由概率公式求解即可.
【解答】解:画树状图如下:
共有9种等可能的结果,其中是偶数的结果有5种,
是偶数的概率为,
故答案为:.
12.(3分)如图,正八边形的边长为4,以顶点为圆心,的长为半径画圆,则阴影部分的面积为 (结果保留.
【分析】先根据正八边形的性质求出圆心角的度数,再根据扇形面积的计算方法进行计算即可.
【解答】解:由题意得,,,
,
故答案为:.
13.(3分)如图,点是正方形内的一点,将绕点按顺时针方向旋转,得到.若,则 80 度.
【分析】先根据正方形的性质可得,从而可得,然后根据旋转的性质可得:,,从而可得,最后利用三角形的外角性质进行计算,即可解答.
【解答】解:四边形是正方形,
,
,
,
由旋转得:,,
,
是的一个外角,
,
故答案为:80.
14.(3分)如图,在四边形中,,,,,点在线段上运动,点在线段上,,则线段的最小值为 .
【分析】设的中点为,以为直径画圆,连接交于,证得,于是得到点在以为直径的半圆上运动,当点运动到与是交点时,线段有最小值,据此解答即可.
【解答】解:设的中点为,以为直径画圆,连接交于,
,
,
,
,
,
点在以为直径的半圆上运动,当点运动到与是交点时,线段有最小值,
,
,
,
线段的最小值为,
故答案为:.
三、解答题(本题共78分,把解答或证明过程写在答题卡的相应区城内.)
15.(6分)解不等式组.
【分析】先解出每个不等式的解集,即可得到不等式组的解集.
【解答】解:,
解不等式①,得:,
解不等式②,得:,
该不等式组的解集是.
16.(6分)先化简,再求值:,其中,满足.
【分析】利用分式的相应的法则对式子进行化简,再代入相应的值运算即可.
【解答】解:
,
,
,
原式.
17.(6分)如图,在中,平分,交于点,平分,交于点.求证:.
【分析】根据平行四边形的性质,,,进而利用角平分线得出,利用证明与全等解答即可.
【解答】证明:四边形是平行四边形,
,,,
平分,交于点,平分,交于点,
,
在与中,
,
,
.
18.(6分)无人机在实际生活中的应用越来越广泛.如图所示,某人利用无人机测量大楼的高度,无人机在空中点处,测得点距地面上点80米,点处的俯角为,楼顶点处的俯角为,已知点与大楼的距离为70米(点,,,在同一平面内),求大楼的高度(结果保留根号).
【分析】过作于,过作于,而,则四边形是矩形,先解,求出,,得到的长度,再解,得到的长
即可解决问题.
【解答】解:如图所示:
过作于,过作于,而,
则四边形是矩形,
,,
由题意可得:,,,,
,,
,
,
,
大楼的高度为.
19.(7分)某班学生以跨学科主题学习为载体,综合运用体育、数学、生物学等知识,研究体育课的运动负荷.在体育课基本部分运动后,测量统计了部分学生的心率情况,按心率次数(次分钟),分为如下五组:组:,组:,组,组:,组:.其中组数据为:73,65,74,68,74,70,66,56.
根据统计数据绘制了不完整的统计图(如图所示),请结合统计图解答下列问题:
(1)组数据的中位数是 69 ,众数是 ;在统计图中组所对应的扇形圆心角是 度;
(2)补全学生心率频数分布直方图;
(3)一般运动的适宜心率为(次分钟),学校共有2300名学生,请你依据此次跨学科研究结果,估计大约有多少名学生达到适宜心率?
【分析】(1)分别根据中位数、众数的定义可得组数据的中位数和众数;用组频数除以组所占百分比可得样本容量,用乘组数据所占比例可得在统计图中组所对应的扇形圆心角度数;
(2)先求出组频数,即可补全学生心率频数分布直方图;
(3)用2300乘样本中组和组所占百分比即可.
【解答】解:(1)把组数据从小到大排列为:56,65,66,68,70,73,74,74,
故组数据的中位数是:,众数是74;
由题意得,样本容量为:,
在统计图中组所对应的扇形圆心角是:.
故答案为:69,74,54;
(2)组频数为:,
补全学生心率频数分布直方图如下:
(3)(名,
答:估计大约有1725名学生达到适宜心率.
20.(7分)如图,已知坐标轴上两点,,连接,过点作,交反比例函数在第一象限的图象于点.
(1)求反比例函数和直线的表达式;
(2)将直线向上平移个单位,得到直线,求直线与反比例函数图象的交点坐标.
【分析】(1)过点作轴于点,先证,求出点的坐标,即可求出反比例函数的解析式和直线的解析式;
(2)先求出直线的解析式,然后与反比例函数的解析式组成方程组,求出方程组的解即得出直线与反比例函数图象的交点坐标.
【解答】解:(1)如图,过点作轴于点,
,
,
,
,
,
,
,
,
,
,
,
,,,
,,,
,
,
,
,
点的坐标是,
反比例函数过点,
,
反比例函数的解析式为;
设直线的解析式为,
其图象经过点,
,
解得,
直线的解析式为;
(2)将直线向上平移个单位,得到直线,
直线的解析式为,
由题意得,,
解得,,
直线与反比例函数图象的交点坐标为或.
21.(10分)某学校为美化学校环境,打造绿色校园,决定用篱笆围成一个一面靠墙(墙足够长)的矩形花园,用一道篱笆把花园分为,两块(如图所示),花园里种满牡丹和芍药.学校已定购篱笆120米.
(1)设计一个使花园面积最大的方案,并求出其最大面积;
(2)在花园面积最大的条件下,,两块内分别种植牡丹和芍药,每平方米种植2株,已知牡丹每株售价25元,芍药每株售价15元,学校计划购买费用不超过5万元,求最多可以购买多少株牡丹?
【分析】(1)设垂直于墙的边为米,根据矩形面积公式得:,由二次函数性质可得答案;
(2)设购买牡丹株,根据学校计划购买费用不超过5万元,列不等式可解得答案.
【解答】解:(1)设垂直于墙的边为米,围成的矩形面积为平方米,则平行于墙的边为米,
根据题意得:,
,
当时,取最大值1200,
,
垂直于墙的边为20米,平行于墙的边为60米,花园面积最大为1200平方米;
(2)设购买牡丹株,则购买芍药株,
学校计划购买费用不超过5万元,
,
解得,
最多可以购买1400株牡丹.
22.(10分)如图,为的直径,是圆上一点,是的中点,弦,垂足为点.
(1)求证:;
(2)是上一点,,,求;
(3)在(2)的条件下,当是的平分线时,求的长.
【分析】(1)由是的中点得由垂径定理得得到,根据同圆中,等 弧对等弦即可证明;
(2)连接,证明,设的半径为,利用相似三角形的性质得,,由勾股定理求得,得到,即可得到;
(3)过点作 交于点,证明是等腰直角三角形,解直角三角形得到,由 得到,解得,即可求解.
【解答】(1)证明:是 的中点,
,
且为的直径,
,
,
;
(2)解:连接,
,
,
为的直径,
,
,
,
,
,
设的半径为,
则,
解得,经检验,是方程的根,
,
,
,
,
;
(3)解:如图,过点作交于点,
,
,是 的平分线,
,
,
,
,
,
.
23.(10分)(1)如图1,在矩形中,点,分别在边,上,,垂足为点.求证:.
【问题解决】
(2)如图2,在正方形中,点,分别在边,上,,延长到点,使,连接.求证:.
【类比迁移】
(3)如图3,在菱形中,点,分别在边,上,,,,求的长.
【分析】(1)由矩形的性质得,再证,即可得出结论;
(2)证,得,再证,得,然后由平行线的性质得,即可得出结论;
(3)延长至点,使,连接,,得,,再证是等边三角形,得,即可解决问题.
【解答】(1)证明:四边形是矩形,
,
,
,
,
,
,
;
(2)证明:四边形是正方形,
,,,
,
,
,
,
,
点在的延长线上,
,
又,
,
,
,
,
;
(3)解:如图3,延长至点,使,连接,
四边形是菱形,
,,
,
,
,,
,
,
是等边三角形,
,
,
,
即的长为3.
24.(10分)已知抛物线与轴交于,两点,与轴交于点,其对称轴为.
(1)求抛物线的表达式;
(2)如图1,点是线段上的一动点,连接,,将沿直线翻折,得到△,当点恰好落在抛物线的对称轴上时,求点的坐标;
(3)如图2,动点在直线上方的抛物线上,过点作直线的垂线,分别交直线,线段于点,,过点作轴,垂足为,求的最大值.
【分析】(1)由题易得的值,再根据对称轴求出的值,即可解答;
(2)过作轴的垂线,垂足为求出和的坐标,得到,由,推出,解直角三角形得到的长,即可解答;
(3)求得所在直线的解析式为,设,设所在直线的解析式为:,得,令,解得,分别表示出和,再 对 进行化简计算,配方成顶点式即可求解.
【解答】解:(1)抛物线与轴交于点,
,
对称轴为,
,,
抛物线的解析式为;
(2)如图,过作轴的垂线,垂足为,
令,
解得:,,
,,
,
由翻折可得,
对称轴为,
,
,
,,
,
在中,,
;
(3)设所在直线的解析式为,
把、坐标代入得:,
解得:,
,
,
,
,
直线与轴所成夹角为,
设,
设所在直线的解析式为:,
把点代入得,
,
令,则,
解得,
,
,
,
点在直线上方,
,
当时,的最大值为.
2020年山东省菏泽市中考数学试卷: 这是一份2020年山东省菏泽市中考数学试卷,共27页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年山东省菏泽市中考数学试卷: 这是一份2023年山东省菏泽市中考数学试卷,共30页。试卷主要包含了填空题,解答题等内容,欢迎下载使用。
2023年山东省菏泽市中考数学试卷: 这是一份2023年山东省菏泽市中考数学试卷,共30页。试卷主要包含了填空题,解答题等内容,欢迎下载使用。












