人教A版 (2019)必修 第二册7.1 复数的概念练习

这是一份人教A版 (2019)必修 第二册7.1 复数的概念练习，共15页。试卷主要包含了复数的实部与虚部，复数的分类，复数相等，复平面及应用，复数几何轨迹等内容，欢迎下载使用。

典例精讲
考点一 复数的实部与虚部
【例1-1】（2022·高一课时练习）若复数的实部与虚部之和为0，则b的值为（ ）
A．2B．C．D．
【例1-2】（2022·高一课时练习）以的虚部为实部，以的实部为虚部的复数是（ ）
A．B．C．D．
【一隅三反】
1．（2022春·福建龙岩·高一上杭县第二中学校考阶段练习）已知复数，则复数z的虚部为（ ）
A．1B．2iC．2D．i
2．（2022·高一课时练习）已知的实部与虚部相等，则实数（ ）
A．2B．C．3D．
3（2022·云南）已知复数的实部大于虚部，则的取值范围为________．
考点二 复数的分类
【例2】（2022天津）已知复数，．
(1)若z是实数，求m的值．
(2)若z是纯虚数，求m的值．
【一隅三反】
1．（2022春·山东聊城·高一山东聊城一中校考期中）已知复数是纯虚数，则实数（ ）
A．B．C．0D．1
2．（2022·高一单元测试）“复数为纯虚数”是“”的（ ）
A．必要非充分条件B．充分非必要条件
C．充要条件D．既非充分也非必要条件
3．（2022·高一课时练习）（多选）下列说法错误的是（ ）
A．复数不是纯虚数
B．若，则复数是纯虚数
C．若是纯虚数，则实数
D．若复数，则当且仅当时，z为虚数
考点三 复数相等
【例3】（2022·贵州·高一校联考阶段练习）设（i是虚数单位，，），若复数，则z为（ ）
A．B．C．D．
【一隅三反】
1．（2022·高一课时练习）若，是虚数单位，，则等于（ ）
A．B．C．D．
2．（2022春·吉林·高一长春市第二实验中学校联考期末）已知，，是虚数单位，若，则（ ）
A．B．2C．1D．0
3．（2022·高一课时练习）（多选）若，且，则等于（ ）
A．4B．C．2D．0
考点四 复平面及应用
【例4-1】（2022·高一课时练习）在复平面内，若复数对应的点的坐标为，则实数（ ）
A．1B．C．2D．
【例4-2】（2022·高一课时练习）在复平面内，复数，则对应的点位于（ ）
A．第一象限B．第二象限
C．第三象限D．第四象限
【例4-3】（2022春·湖北·高一宜昌市夷陵中学校联考期中）已知复数在复平面内对应的点在第三象限，则实数的取值范围是（ ）
A．B．C．D．
【例4-4】（2022·高一课时练习）复数，则（ ）
A．在复平面内对应的点的坐标为
B．在复平面内对应的点的坐标为
C．
D．
【一隅三反】
1．（2022·高一课时练习）在复平面内，复数z对应的点在第四象限，对应向量的模为3，且实部为，则复数z等于（ ）
A．B．C．D．
2．（2022春·黑龙江·高一哈九中校考期中）已知为虚数单位，复数，则下列命题不正确的是（ ）
A．的共轭复数为B．的虚部为
C．在复平面内对应的点在第一象限D．
3．（2022·高一课时练习）当时，复数在复平面上对应的点位于（ ）．
A．第一象限B．第二象限C．第三象限D．第四象限
4．（2022·高一课时练习）在复平面内，复数z对应的点在第四象限，若，则（ ）
A．B．C．D．
考点五 复数几何轨迹
【例5-1】（2022春·吉林长春·高一校考期中）已知是虚数单位，复数，且，则的最大值为（ ）
A．1B．2C．3D．4
【例5-2】（2022春·上海金山·高一上海市金山中学校考期末）已知复数满足，则在复平面内复数对应的点所在区域的面积为_____．
【一隅三反】
1．（2023·高一课时练习）复平面上复数满足，则复数对应的点的轨迹是（ ）．
A．抛物线B．直线C．线段D．圆
2．（2022春·广东东莞·高一统考期末）复数在复平面内对应的点为，若，则点的集合对应的图形的面积为（ ）
A．B．C．D．
3（2022春·湖北武汉·高一华中师大一附中校考阶段练习）已知复数z的共轭复数，满足，则的最小值为（ ）
A．4B．8C．D．
7.1 复数的概念（精讲）
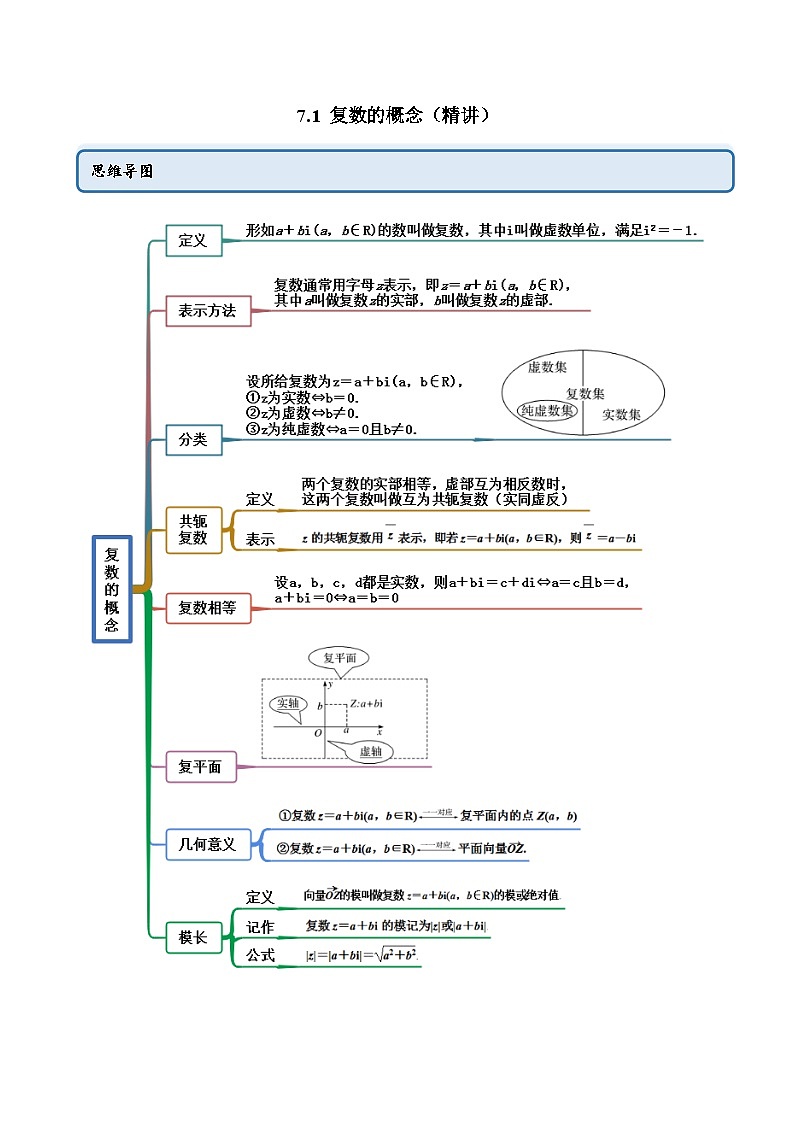
思维导图
典例精讲
考点一 复数的实部与虚部
【例1-1】（2022·高一课时练习）若复数的实部与虚部之和为0，则b的值为（ ）
A．2B．C．D．
【答案】A
【解析】由复数的实部与虚部之和为0，得，即．故选：A
【例1-2】（2022·高一课时练习）以的虚部为实部，以的实部为虚部的复数是（ ）
A．B．C．D．
【答案】A
【解析】设所求复数为，由题意知复数的虚部为7，所以，
复数的实部为，所以，故．故选：A.
【一隅三反】
1．（2022春·福建龙岩·高一上杭县第二中学校考阶段练习）已知复数，则复数z的虚部为（ ）
A．1B．2iC．2D．i
【答案】C
【解析】根据复数的概念可知，复数的虚部为.故选：C
2．（2022·高一课时练习）已知的实部与虚部相等，则实数（ ）
A．2B．C．3D．
【答案】D
【解析】由题可知，解得.故选：D．
3（2022·云南）已知复数的实部大于虚部，则的取值范围为________．
【答案】
【解析】由已知可得，即，解得或．
因此，的取值范围是．故答案为：．
考点二 复数的分类
【例2】（2022天津）已知复数，．
(1)若z是实数，求m的值．
(2)若z是纯虚数，求m的值．
【答案】(1)或；(2)；
【解析】（1）因为为实数，所以，解得或.
（2）因为是纯虚数，所以有，解得.
【一隅三反】
1．（2022春·山东聊城·高一山东聊城一中校考期中）已知复数是纯虚数，则实数（ ）
A．B．C．0D．1
【答案】B
【解析】，因为复数是纯虚数，所以，且，解得.
故选：B
2．（2022·高一单元测试）“复数为纯虚数”是“”的（ ）
A．必要非充分条件B．充分非必要条件
C．充要条件D．既非充分也非必要条件
【答案】B
【解析】由纯虚数的概念可知，若复数为纯虚数，则且，故“复数为纯虚数”是“”的充分不必要条件.
故选：B
3．（2022·高一课时练习）（多选）下列说法错误的是（ ）
A．复数不是纯虚数
B．若，则复数是纯虚数
C．若是纯虚数，则实数
D．若复数，则当且仅当时，z为虚数
【答案】ACD
【解析】时，复数是纯虚数，A错误；
当时，复数是纯虚数，B正确；
是纯虚数，则即，C错误；
复数未注明为实数，D错误．
故选：ACD．
考点三 复数相等
【例3】（2022·贵州·高一校联考阶段练习）设（i是虚数单位，，），若复数，则z为（ ）
A．B．C．D．
【答案】A
【解析】因为（i是虚数单位，，），所以，所以.故选：A
【一隅三反】
1．（2022·高一课时练习）若，是虚数单位，，则等于（ ）
A．B．C．D．
【答案】D
【解析】因为，所以，，即，，
所以．故选：D．
2．（2022春·吉林·高一长春市第二实验中学校联考期末）已知，，是虚数单位，若，则（ ）
A．B．2C．1D．0
【答案】D
【解析】因为，所以，所以，所以．故选：D.
3．（2022·高一课时练习）（多选）若，且，则等于（ ）
A．4B．C．2D．0
【答案】AD
【解析】因为，且，
所以，解得或，所以或0．故选：AD
考点四 复平面及应用
【例4-1】（2022·高一课时练习）在复平面内，若复数对应的点的坐标为，则实数（ ）
A．1B．C．2D．
【答案】D
【解析】复数对应的点的坐标为由题干得到 故选：D.
【例4-2】（2022·高一课时练习）在复平面内，复数，则对应的点位于（ ）
A．第一象限B．第二象限
C．第三象限D．第四象限
【答案】B
【解析】由，可得，在复平面内，复数对应的点为，位于第二象限
故选：B
【例4-3】（2022春·湖北·高一宜昌市夷陵中学校联考期中）已知复数在复平面内对应的点在第三象限，则实数的取值范围是（ ）
A．B．C．D．
【答案】D
【解析】因为复数在复平面内对应的点在第三象限，
所以，解得，所以实数的取值范围为.故选：D.
【例4-4】（2022·高一课时练习）复数，则（ ）
A．在复平面内对应的点的坐标为
B．在复平面内对应的点的坐标为
C．
D．
【答案】AD
【解析】在复平面内对应的点的坐标为，．故选：AD.
【一隅三反】
1．（2022·高一课时练习）在复平面内，复数z对应的点在第四象限，对应向量的模为3，且实部为，则复数z等于（ ）
A．B．C．D．
【答案】D
【解析】设，则，解得，所以．故选：D.
2．（2022春·黑龙江·高一哈九中校考期中）已知为虚数单位，复数，则下列命题不正确的是（ ）
A．的共轭复数为B．的虚部为
C．在复平面内对应的点在第一象限D．
【答案】B
【解析】由题知，复数的共轭复数为，虚部为1，在复平面内对应的点为在第一象限，，故B错误故选：B
3．（2022·高一课时练习）当时，复数在复平面上对应的点位于（ ）．
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】D
【解析】∵，∴，，
∴复数在复平面上对应的点位于第四象限．故选：D.
4．（2022·高一课时练习）在复平面内，复数z对应的点在第四象限，若，则（ ）
A．B．C．D．
【答案】D
【解析】由题意，得，则，解得（2舍去），所以.
故选：D.
考点五 复数几何轨迹
【例5-1】（2022春·吉林长春·高一校考期中）已知是虚数单位，复数，且，则的最大值为（ ）
A．1B．2C．3D．4
【答案】C
【解析】若,即,点为圆上的点,
，则其几何意义为圆上的点到点之间的距离,
则的最大值为故选：C.
【例5-2】（2022春·上海金山·高一上海市金山中学校考期末）已知复数满足，则在复平面内复数对应的点所在区域的面积为_____．
【答案】
【解析】设，，
因为，所以，
所以，
所以复平面内复数对应的点所在区域是圆和圆围成的圆环，
故所求区域面积.
故答案为：.
【一隅三反】
1．（2023·高一课时练习）复平面上复数满足，则复数对应的点的轨迹是（ ）．
A．抛物线B．直线C．线段D．圆
【答案】C
【解析】设，
因为，所以，
该式表示动点到定点的距离之和为（与两定点间的距离相等），
所以复数对应的点的轨迹为以为端点的线段.
故选：C.
2．（2022春·广东东莞·高一统考期末）复数在复平面内对应的点为，若，则点的集合对应的图形的面积为（ ）
A．B．C．D．
【答案】C
【解析】因为复数在复平面内对应的点为，且，
所以点的集合对应的图形是一个内半径为1，外半径为2的圆环，
所以所求面积为，
故选：C
3（2022春·湖北武汉·高一华中师大一附中校考阶段练习）已知复数z的共轭复数，满足，则的最小值为（ ）
A．4B．8C．D．
【答案】A
【解析】设（是虚数单位）.则.
因为，所以表示点(x,y)在以（-4，-2）为圆心，1为半径的圆上.
而表示圆上任意一点到（0，1）的距离.
由几何法可知：的最小值为（0，1）到圆心（-4，-2）减去圆的半径，即为.
故选：A