

人教A版 (2019)必修 第二册8.5 空间直线、平面的平行达标测试
展开A.一条直线不相交B.两条相交直线不相交
C.无数条直线不相交D.任意一条直线不相交
2.(2023云南)如图,在四棱柱中,平面平面,且,则四边形的形状是( )
A.平行四边形B.矩形C.菱形D.正方形
3.(2022上海)在三棱锥中,点E,F分别在上.若,则直线与平面的位置关系为( )
A.平行B.相交C.平面D.不能确定
4.(2022山东)如果,表示直线,,表示平面,那么下列说法中正确的是( )
A.若,,则B.若,,则
C.若,,则D.若,,,则
5.(2022湖北)下列条件中,能得出直线与平面平行的是( )
A.直线与平面内的所有直线平行
B.直线与平面内的无数条直线平行
C.直线与平面没有公共点
D.直线与平面内的一条直线平行
6.(2022河南)如图,已知平面平面,点为,外一点,直线,分别与,相交于,和,,则与的位置关系为( )
A.平行B.相交C.异面D.平行或异面
7.(2022北京)已知为三条不重合的直线,为两个不重合的平面,下列命题正确的是( )
A.若,,则B.若,,则
C.若,,则D.若,,则
8.(2022湖北)已知正方体,下列结论中,正确的是______.(填序号)
①;②;③平面.
9.(2022河南)长方体的底面是正方形,,分别是侧棱,上的动点,,在棱上,且.若平面,则_________.
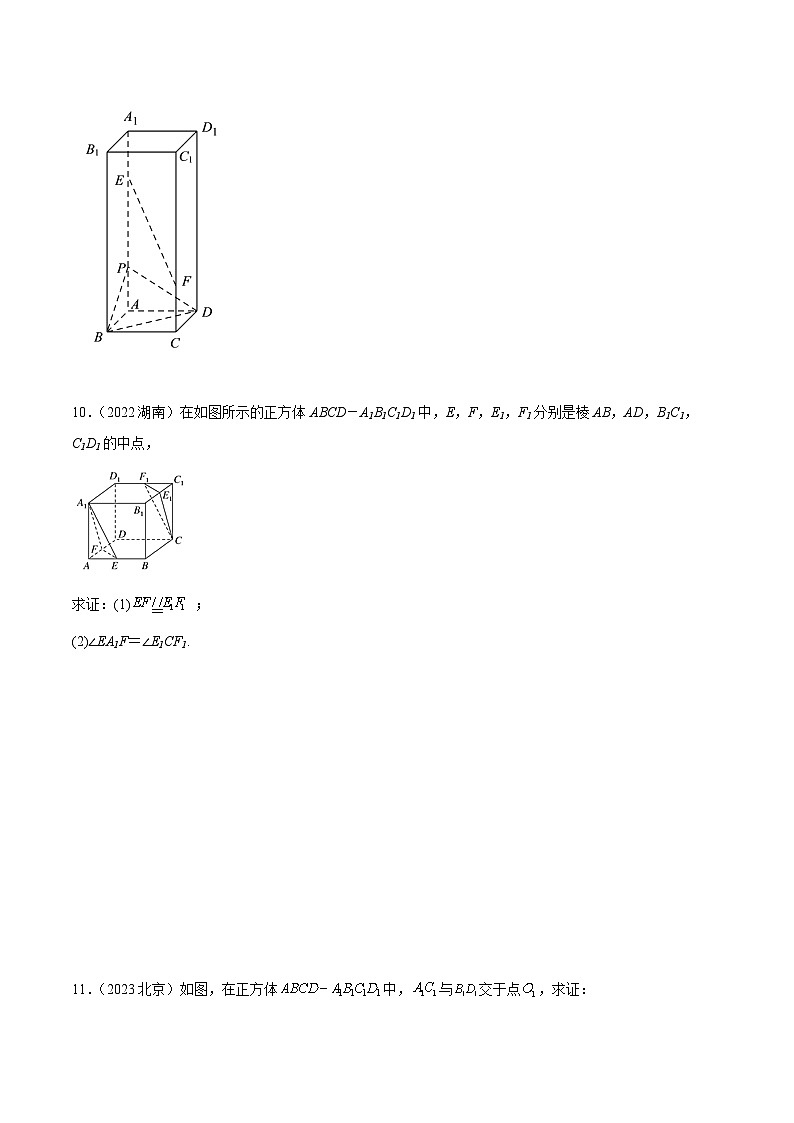
10.(2022湖南)在如图所示的正方体ABCD-A1B1C1D1中,E,F,E1,F1分别是棱AB,AD,B1C1,C1D1的中点,
求证:(1) ;
(2)∠EA1F=∠E1CF1.
11.(2023北京)如图,在正方体中,与交于点,求证:
(1)直线平面;
(2)直线平面.
12.(2022哈尔滨)如图,M,N,K分别是正方体的棱的中点.求证:∥平面.
13.(2022西藏)如图所示,在四棱柱中,已知,.在DC上是否存在一点E,使平面?若存在,试确定点E的位置;若不存在,请说明理由.
14.(2022甘肃)如图,在五面体中,,底面ABC是正三角形,.四边形是矩形,问:D在AC上运动,当D在何处时,有平面,并说明理由.
15.(2022陕西)如图,在正方体中,是的中点,分别是的中点,求证:
(1)平面;
(2)平面平面.
16.(2022福建)如图所示,在正方体中,,,分别是,,的中点.求证:平面平面.
17.(2022陕西省)如图,四棱锥的底面是正方形,PA⊥平面ABCD,E,F分别为AB,PD的中点,且PA=AD=2.
(1)求证:平面PEC;
(2)求三棱锥的体积.
18(2022四川省)如图,在四棱柱ABCD﹣A1B1C1D1中,点M是线段B1D1上的一个动点,E,F分别是BC,CM的中点.
(1)求证:EF平面BDD1B1;
(2)设G为棱CD上的中点,求证:平面GEF平面BDD1B1.
19(2022北京)如图,在三棱柱中,,,分别为,,的中点.
(1)求证:平面平面;
(2)若平面,求证:为的中点.
20.(2022湖北)如图,正方体中,、、、分别是相应棱的中点,证明:平面平面.
21.(2022黑龙江)如图,四棱锥中,,,为的中点.
(1)求证:平面.
(2)在线段上是否存在一点,使得平面平面?若存在,证明你的结论,若不存在,请说明理由.
22.(2023山东省)如图,四棱锥中,,,点为上一点,为,且平面.
(1)若平面与平面的交线为,求证:平面;
(2)求证:.
1.(2022山东省)(多选)如图,点P在正方体的面对角线上运动,则下列四个结论一定正确的有( )
A.∥B.∥面
C.∥面D.三棱锥的体积不变
2.(2022辽宁)如图,在正方体中,为线段上任意一点(包括端点),则一定有( )
A.与异面B.与相交
C.与平面平行D.与平面相交
3(2022天津)如图,在棱长为的正方体中,、分别是棱、的中点,是侧面上一点,若平面,则线段长度的取值范围是( )
A.B.C.D.
4.(2022上海)如图,在长方体中,
分别为的中点.点在平面内,若直线平面,则线段长度的最小值是______・
5.(2022辽宁)如图,三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=AB.
(1)求证:EF∥平面BDC1;
(2)在棱AC上是否存在一个点G,使得平面EFG将三棱柱分割成的两部分体积之比为1:15,若存在,指出点G的位置;若不存在,说明理由.
6.(2023重庆)如图所示,在正方体中,点N在BD上,点M在上,且,求证:平面.
7.(2022浙江)如图,在长方体中,,E为CD中点.问:在棱上是否存在一点P,使得平面?若存在,求AP的长;若不存在,说明理由.
8.(2022黑龙江)如图,平面平面平面,异面直线 分别与平面 相交于点和点.已知,,,求、、的长.
8.5 空间直线、平面的平行(精练)
1.(2022广西)如果直线平面,那么直线与平面内的( )
A.一条直线不相交B.两条相交直线不相交
C.无数条直线不相交D.任意一条直线不相交
【答案】D
【解析】由线面平行定义知:直线与平面无交点,直线与平面内的任意一条直线不相交.
故选:D.
2.(2023云南)如图,在四棱柱中,平面平面,且,则四边形的形状是( )
A.平行四边形B.矩形C.菱形D.正方形
【答案】A
【解析】,四点共面;
平面平面,平面平面,平面平面,,
四边形为平行四边形.故选:A.
3.(2022上海)在三棱锥中,点E,F分别在上.若,则直线与平面的位置关系为( )
A.平行B.相交C.平面D.不能确定
【答案】A
【解析】因为,所以.
又平面平面,所以平面.故选:A
4.(2022山东)如果,表示直线,,表示平面,那么下列说法中正确的是( )
A.若,,则B.若,,则
C.若,,则D.若,,,则
【答案】D
【解析】A中,也可能成立;B中,,还有可能相交或异面;
C中,也可能成立;由直线与平面平行的性质定理可知D正确.故选:D
5.(2022湖北)下列条件中,能得出直线与平面平行的是( )
A.直线与平面内的所有直线平行
B.直线与平面内的无数条直线平行
C.直线与平面没有公共点
D.直线与平面内的一条直线平行
【答案】C
【解析】对A,直线与平面内的所有直线平行不可能,故A错误;
对B,当直线在平面内时,满足直线与平面内的无数条直线平行,但与不平行;
对C,能推出与平行;
对D,当直线在平面内时,与不平行.故选:C.
6.(2022河南)如图,已知平面平面,点为,外一点,直线,分别与,相交于,和,,则与的位置关系为( )
A.平行B.相交C.异面D.平行或异面
【答案】A
【解析】由题意知,,,,在同一平面内,且平面平面,平面平面,且,∴,故选:A.
7.(2022北京)已知为三条不重合的直线,为两个不重合的平面,下列命题正确的是( )
A.若,,则B.若,,则
C.若,,则D.若,,则
【答案】D
【解析】对于A选项,若,,则可能相交,A选项错误.
对于B选项,若,,则可能,B选项错误.
对于C选项,若,,则可能,C选项错误.
对于D选项,若,,根据平行的传递性可知,所以D选项正确.
故选:D
8.(2022湖北)已知正方体,下列结论中,正确的是______.(填序号)
①;②;③平面.
【答案】①③
【解析】因为,,所以四边形为平行四边形,故,故①正确;
如果,而,所以,而,因此不可能成立,故②错误;因为,平面,平面,所以平面,故③正确.
故答案为:①③
9.(2022河南)长方体的底面是正方形,,分别是侧棱,上的动点,,在棱上,且.若平面,则_________.
【答案】2
【解析】连接,交于点,连接,过点作,交于点.
∵平面,平面,平面平面,
∴.
∵,
∴,又,
∴四边形为平行四边形,
∴.
∵四边形是正方形,
∴是的中点,
又,∴.
∵,
∴.
故答案为:2
10.(2022湖南)在如图所示的正方体ABCD-A1B1C1D1中,E,F,E1,F1分别是棱AB,AD,B1C1,C1D1的中点,
求证:(1) ;
(2)∠EA1F=∠E1CF1.
【答案】(1)见解析;(2)见解析
【解析】(1)连接,,在中,因为,分别为,的中点,
所以,同理,在正方体中,因为,,所以,所以四边形是平行四边形,所以,所以.
(2)取的中点,连接,因为,,所以,
所以四边形是平行四边形,所以,因为,所以四边形是平行四边形,所以,所以,同理可证:,又与两边的方向均相反,所以.
11.(2023北京)如图,在正方体中,与交于点,求证:
(1)直线平面;
(2)直线平面.
【答案】(1)证明见解析(2)证明见解析
【解析】(1)证明:直线在平面外,因为,
所以四边形是平行四边形,所以,
而是平面内的直线,根据判定定理可知,直线平面.
(2)证明:如图,连接BD,交AC于O,连接,易知,
则四边形是平行四边形,所以,
所以在平面上,根据判定定理可知,平面.
12.(2022哈尔滨)如图,M,N,K分别是正方体的棱的中点.求证:∥平面.
【答案】证明见解析
【解析】证明:连接.因为N,K分别为的中点,所以且,
于是四边形为平行四边形,所以.
因为平面,平面,所以∥平面.
13.(2022西藏)如图所示,在四棱柱中,已知,.在DC上是否存在一点E,使平面?若存在,试确定点E的位置;若不存在,请说明理由.
【答案】存在,理由见解析
【解析】存在,当点E是DC的中点时,有平面.
连接BE,∵E是DC的中点,∴.
又∵,,∴,
∴四边形为平行四边形,
∴.
又∵,∴,
∴四边形为平行四边形,
∴.
又∵平面,平面,
∴平面.
14.(2022甘肃)如图,在五面体中,,底面ABC是正三角形,.四边形是矩形,问:D在AC上运动,当D在何处时,有平面,并说明理由.
【答案】D为AC中点时,理由见解析
【解析】当D为AC中点时,平面.
理由:连接与交于点O,当D为AC中点时,,且OD是平面上的直线,而是平面外的直线,根据直线与平面平行的判定定理可知,平面.
15.(2022陕西)如图,在正方体中,是的中点,分别是的中点,求证:
(1)平面;
(2)平面平面.
【答案】(1)证明见解析(2)证明见解析
【解析】(1)
如图,连接,∵分别是的中点,∴.
又∵平面,平面,∴直线平面.
(2)连接SD,∵分别是 的中点,
∴.又∵平面,平面,
∴平面,由(1)知,平面,
且平面,平面,,
∴平面∥平面.
16.(2022福建)如图所示,在正方体中,,,分别是,,的中点.求证:平面平面.
【答案】证明见解析
【解析】证明:如图,连接.
因为,分别是,的中点,所以.
因为∥,,
所以四边形为平行四边形,
所以,
所以.
因为平面,平面,
所以平面.
同理可证平面.
又因为,,平面,
所以平面平面.
17.(2022陕西省)如图,四棱锥的底面是正方形,PA⊥平面ABCD,E,F分别为AB,PD的中点,且PA=AD=2.
(1)求证:平面PEC;
(2)求三棱锥的体积.
【答案】(1)证明见解析;(2)
【解析】(1)取PC的中点G,连接EG,FG,
因为F是的中点,
所以,
因为E是AB的中点,
所以,
所以,
所以四边形是平行四边形,
所以,
因为平面,平面,
所以平面;
(2)因为PA⊥平面ABCD,F为PD的中点,且PA=AD=2,四边形ABCD是正方形,
所以三棱锥的体积为:
=.
18(2022四川省)如图,在四棱柱ABCD﹣A1B1C1D1中,点M是线段B1D1上的一个动点,E,F分别是BC,CM的中点.
(1)求证:EF平面BDD1B1;
(2)设G为棱CD上的中点,求证:平面GEF平面BDD1B1.
【答案】(1)证明见解析(2)证明见解析
【解析】(1)证明:在四棱柱ABCD﹣A1B1C1D1中,连接BM,如图,
因E,F分别是BC,CM的中点,
则有EFBM,
又EF平面BDD1B1,BM平面BDD1B1,
所以EF平面BDD1B1.
(2)证明:取CD的中点G,连接EG,FG,如图,
而E是BC的中点,
于是得EGBD,
而EG平面BDD1B1,BD平面BDD1B1,
从而得EG平面BDD1B1,
由(1)知EF平面BDD1B1,
EFEG=E,且EF、EG平面GEF,
因此,平面GEF平面BDD1B1,
所以当G是DC的中点时,
平面GEF平面BDD1B1.
19(2022北京)如图,在三棱柱中,,,分别为,,的中点.
(1)求证:平面平面;
(2)若平面,求证:为的中点.
【答案】(1)证明见解析;
(2)证明见解析.
【解析】(1)证明:如图,
,分别为,的中点,
,
平面,平面,
平面,
又,分别为,的中点,
,
又,四边形为平行四边形,则,
平面,平面,
平面,
又,平面,
平面平面;
(2)证明:平面平面,平面平面,
平面与平面有公共点,则有经过的直线,交于G,
则,得,
为的中点,
为的中点.
20.(2022湖北)如图,正方体中,、、、分别是相应棱的中点,证明:平面平面.
【答案】证明见解析
【解析】证明:连接,由题得,
又
所以四边形是平行四边形,所以,
所以,
平面,平面,
平面,
在正方形中,,分别是棱,的中点,
且,
又 且,
且,
四边形是平行四边形,
,
又平面,平面,
平面,
平面,平面,且,
平面平面.
21.(2022黑龙江)如图,四棱锥中,,,为的中点.
(1)求证:平面.
(2)在线段上是否存在一点,使得平面平面?若存在,证明你的结论,若不存在,请说明理由.
【答案】(1)证明见解析
(2)存在,证明见解析
【解析】(1)证明:如图所示,取的中点,连接,.
因为为的中点,
所以,.
又,,
所以,.
因此四边形是平行四边形,
所以.
又平面,平面,
因此平面.
(2)解:如图所示,取的中点,连接,,
所以
又,所以.
又,所以四边形为平行四边形,
因此.
又平面,所以平面.
由(1)可知平面.
因为,故平面平面.
22.(2023山东省)如图,四棱锥中,,,点为上一点,为,且平面.
(1)若平面与平面的交线为,求证:平面;
(2)求证:.
【答案】(1)证明见解析
(2)证明见解析
【解析】(1)∵,平面平面,∴平面.
∵平面,平面平面,∴.
∵平面平面,
∴平面.
(2)连接,设,,连接,
∵平面平面,平面平面,
∴,
∵,,所以,
∴,
∴点是的重心,
∴点是的中点,
∴,
∴,
∴.
1.(2022山东省)(多选)如图,点P在正方体的面对角线上运动,则下列四个结论一定正确的有( )
A.∥B.∥面
C.∥面D.三棱锥的体积不变
【答案】BCD
【解析】对于A,因为平面∥平面,平面平面,平面平面,
所以∥,所以当为的中点时,才有∥,所以A错误,
对于B,因为平面∥平面,平面,所以∥面,所以B正确,
对于C,由选项A同理可得∥,因为平面,平面,所以∥面,所以C正确,
对于D,因为由选项C可知∥,因为平面,平面,
所以∥平面,所以点到平面为常数,
因为三角形的面积为常数,所以为定值,
因为,所以三棱锥的体积不变,所以D正确,
故选:BCD.
2.(2022辽宁)如图,在正方体中,为线段上任意一点(包括端点),则一定有( )
A.与异面B.与相交
C.与平面平行D.与平面相交
【答案】C
【解析】连接、,因为且,所以,四边形为平行四边形,
当为、的交点时,与相交,
当不为、的交点时,与异面,AB选项都不一定成立;
连接、,因为且,故四边形为平行四边形,
,平面,平面,平面,
同理可证平面,
因为,、平面,平面平面,
平面,平面,C选项一定满足,D选项一定不满足.
故选:C.
3(2022天津)如图,在棱长为的正方体中,、分别是棱、的中点,是侧面上一点,若平面,则线段长度的取值范围是( )
A.B.C.D.
【答案】B
【解析】如图所示,分别取棱、的中点、,连接、、、、,
因为、分别为、的中点,则,同理可得,,
平面,平面,平面,
因为且,、分别为、的中点,则且,
所以,四边形为平行四边形,所以,且,
且,且,
所以,四边形为平行四边形,,
平面,平面,平面,
,、平面,所以,平面平面,
当时,平面,则平面,
所以,点的轨迹为线段.
在中,.
在中,.
同理,在中,可得,所以,为等腰三角形.
设的中点为,连接.
当点位于的中点处时,,此时最短;当点位于、处时,最长.
易求得,
因此,线段长度的取值范围是.
故选:B.
4.(2022上海)如图,在长方体中,
分别为的中点.点在平面内,若直线平面,则线段长度的最小值是______・
【答案】
【解析】如图,连结,
∵分别为的中点,
∴平面,平面,
∴平面
∵平面,平面,
∴平面,
∵,∴平面平面,
∵平面,
∴点在直线上,在中,,
∴当时,线段的长度最小,最小值为=.
故答案为:.
5.(2022辽宁)如图,三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=AB.
(1)求证:EF∥平面BDC1;
(2)在棱AC上是否存在一个点G,使得平面EFG将三棱柱分割成的两部分体积之比为1:15,若存在,指出点G的位置;若不存在,说明理由.
【答案】(1)证明见解析
(2)点G不存在,理由见解析
【解析】(1)证明:取AB的中点M,
∵AF=AB,
∴F为AM的中点,
又∵E为AA1的中点,
∴EF∥A1M
在三棱柱ABC﹣A1B1C1中,D,M分别为A1B1,AB的中点,
∴A1D∥BM,A1D=BM,
∴A1DBM为平行四边形,∴AM∥BD
∴EF∥BD.
∵BD⊂平面BC1D,EF⊄平面BC1D,
∴EF∥平面BC1D.
(2)设AC上存在一点G,使得平面EFG将三棱柱分割成两部分的体积之比为1:15,则,
∵
∴,
∴,
∴AG=AC>AC.
所以符合要求的点G不存在.
6.(2023重庆)如图所示,在正方体中,点N在BD上,点M在上,且,求证:平面.
【答案】证明见解析
【解析】证明 证法一:如图所示,作,交于点E,作,交AB于点F,连接EF,
则平面,且,.
∵在正方体中,,,
∴.
∴.
,∴.
又,
∴四边形为平行四边形,∴.
∵平面,平面,
∴平面.
证法二:如图所示,连接CN并延长交BA所在直线于点P,连接,
则平面.易知,
∴,
又,,∴,
∴,∴.
∵平面,平面,
∴平面.
7.(2022浙江)如图,在长方体中,,E为CD中点.问:在棱上是否存在一点P,使得平面?若存在,求AP的长;若不存在,说明理由.
【答案】存在,.
【解析】在棱上存在一点P,使得平面.求AP的长如下:
取中点F,连接,,取中点,连接,
当P在中点时,连接,
因为分别是中点,,
又长方体中,与平行且相等,是平行四边形,所以,则,,与共面,
分别是中点,则与平行且相等,而与平行且相等,因此与平行且相等,是平行四边形,,
在矩形上,与平行且相等,是平行四边形,,
所以,
是平面上的直线,PD是平面外的直线,所以平面.因为P为的中点,所以.
8.(2022黑龙江)如图,平面平面平面,异面直线 分别与平面 相交于点和点.已知,,,求、、的长.
【答案】,,
【解析】连接交平面于点,连接,,
因为平面平面,平面平面于,平面平面于,
所以,所以,,
又因为,所以,
所以,
因为,,所以,,
所以,
因为平面平面,平面平面于,平面平面于,
所以,所以,,
又因为,所以,
所以,因为,所以,
所以,所以,
又因为,所以,
所以,,.
高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直一课一练: 这是一份高中数学人教A版 (2019)必修 第二册<a href="/sx/tb_c4000306_t7/?tag_id=28" target="_blank">8.6 空间直线、平面的垂直一课一练</a>,共40页。试卷主要包含了如图,在正方体中,求证等内容,欢迎下载使用。
人教A版 (2019)必修 第二册第八章 立体几何初步8.5 空间直线、平面的平行同步达标检测题: 这是一份人教A版 (2019)必修 第二册<a href="/sx/tb_c4000305_t7/?tag_id=28" target="_blank">第八章 立体几何初步8.5 空间直线、平面的平行同步达标检测题</a>,共42页。试卷主要包含了线线平行,等角性质,线面平行,面面平行,判断定理与性质定理辨析,距离相关问题等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第二册8.5 空间直线、平面的平行练习: 这是一份高中数学人教A版 (2019)必修 第二册<a href="/sx/tb_c4000305_t7/?tag_id=28" target="_blank">8.5 空间直线、平面的平行练习</a>,共34页。试卷主要包含了直线与直线平行,直线和平面平行的判定,填空题,解答题等内容,欢迎下载使用。













