人教A版 (2019)必修 第二册第八章 立体几何初步8.5 空间直线、平面的平行同步达标检测题

这是一份人教A版 (2019)必修 第二册第八章 立体几何初步8.5 空间直线、平面的平行同步达标检测题，共42页。试卷主要包含了线线平行，等角性质，线面平行，面面平行，判断定理与性质定理辨析，距离相关问题等内容，欢迎下载使用。

典例精讲
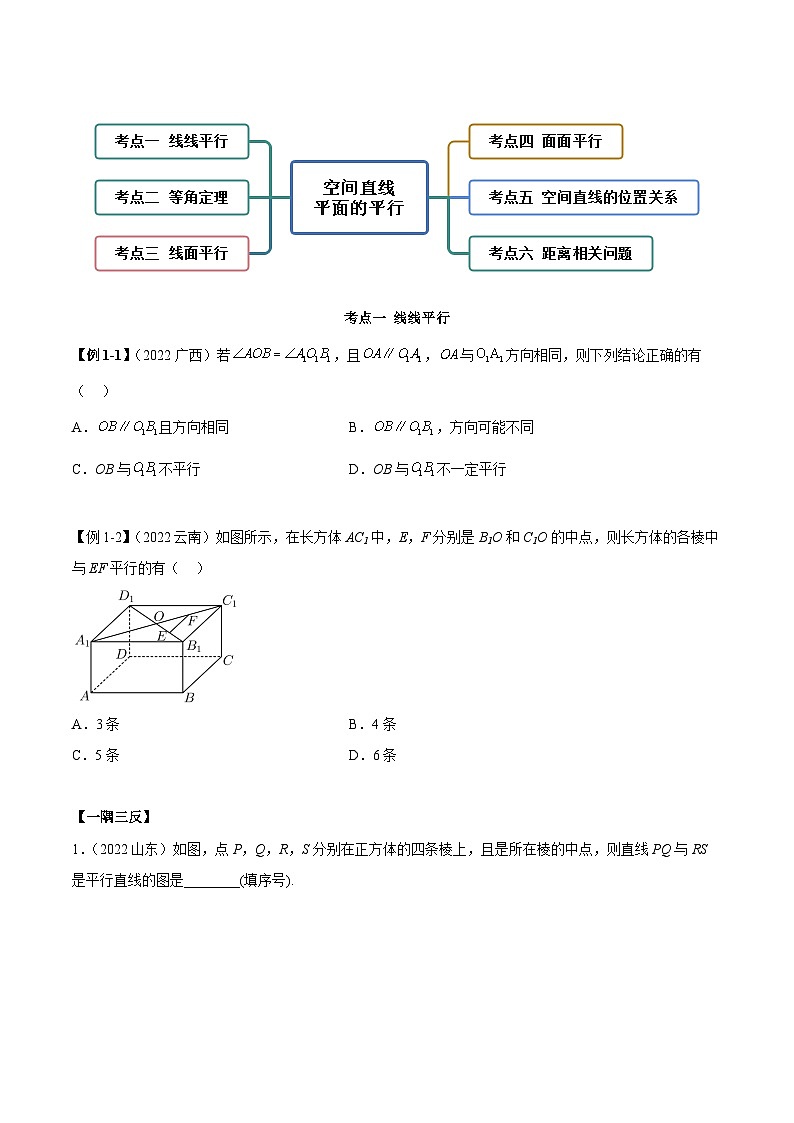
考点一 线线平行
【例1-1】（2022广西）若，且，与方向相同，则下列结论正确的有（ ）
A．且方向相同B．，方向可能不同
C．OB与不平行D．OB与不一定平行
【例1-2】（2022云南）如图所示，在长方体AC1中，E，F分别是B1O和C1O的中点，则长方体的各棱中与EF平行的有（ ）
A．3条B．4条
C．5条D．6条
【一隅三反】
1．（2022山东）如图，点P，Q，R，S分别在正方体的四条棱上，且是所在棱的中点，则直线PQ与RS是平行直线的图是________(填序号).
2（2022黑龙江）如图所示，在三棱柱中，，，，分别是，，，的中点，求证：,,,四点共面.
3．（2022甘肃）如图，E，F分别是长方体ABCD­A1B1C1D1的棱A1A，C1C的中点．求证：四边形B1EDF为平行四边形．
考点二 等角性质
【例2-1】（2022北京）已知，，，则（ ）
A．B．或
C．D．或
【例2-2】（2022广东省连平县）如图，在正方体中，，分别是棱和的中点．
（1）求证：四边形为平行四边形；
（2）求证：．
【一隅三反】
1．（2022湖南）下列结论，其中正确的是________(填序号).
①如果一个角的两边与另一个角的两边分别平行，那么这两个角相等.
②如果两个角的两边都平行于一个平面，那么这两角相等或互补.
③如果一个角的两边和另一个角的两边分别垂直，那么这两个角相等或互补.
④如果两条直线同时平行于第三条直线，那么这两条直线互相平行.
2．（2022浙江）如图，三棱柱中，，，分别为，，的中点.求证：.

3．（2022江苏）长方体中，分别为棱的中点.
（1）求证：；
（2）求证：.
考点三 线面平行
【例3-1】（2022四川）如图，四棱锥中，底面为边长为2的菱形且对角线与交于点O，底面，点E是的中点．
(1)求证：∥平面；
(2)若三棱锥的体积为，求的长．
【例3-2】（2022河北）如图，在四棱柱中，底面ABCD是等腰梯形，，，，，E、、F分别为棱AD、、AB的中点．证明：直线平面．
【例3-3】（2022山东省）如图，四棱锥的底面为平行四边形，分别为的中点.
(1)证明：AF平面；
(2)在线段上是否存在一点，使得平面，并给出必要的证明.
【一隅三反】
1．（2022吉林）在正方体中，分别是的中点，则下列说法中错误的是（ ）
A．平面B．平面
C．平面D．平面
2．（2022上海）如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是（ ）
A．B．C．D．
3.（2022山东省）如图所示，正四棱锥P—ABCD的各棱长均为13，M为PA上的点，且PM∶MA=5∶8.
(1)在线段BD上是否存在一点N，使直线MN平面PBC？如果存在，求出BN∶ND的值，如果不存在，请说明理由；
(2)假设存在满足条件（1）的N点，求线段MN的长.
4．（2022山东省）如图，在四棱锥中，底面为平行四边形，是上一点，当点满足条件：________时，平面.
考点四 面面平行
【例4-1】（2022陕西省）如图，在三棱柱中，分别为的中点，．求证：
(1)平面；
(2)平面平面．
【例4-2】．（2022海南）（多选）在正方体中，下列四组面中彼此平行的有（ ）
A．平面与平面B．平面与平面
C．平面与平面D．平面与平面
【一隅三反】
1．（2022北京）如图，在长方体中，写出满足条件的一个平面：
（1）与平面平行的平面为______；
（2）与平面平行的平面为______；
（3）与平面平行的平面为______．
2．（2022山东省）如图：在正方体中，为的中点.
(1)求证：平面；
(2)若为的中点，求证：平面平面.
3（2022山东省）由四棱柱截去三棱锥后得到的几何体如图所示，四边形为平行四边形，O为与的交点．
(1)求证：∥平面；
(2)求证：平面∥平面；
(3)设平面与底面的交线为l，求证：．
考点五 判断定理与性质定理辨析
【例5-1】（2022广东）已知为不同的平面，a，b为不同的直线，那么下列条件中能推出与平行的是（ ）
A．内有无数条直线与平行B．
C．直线，且D．内任何直线都与平行
【例5-2】（2022山东省）已知为三条不重合的直线，是两个不重合的平面，给出下列四个说法：
①，则；
②，则；
③，则；
④，则.
其中正确的是（ ）
A．①④B．①②C．②④D．③④
【一隅三反】
1．（2022陕西省）下列条件中能推出平面平面的是（ ）
A．存在一条直线，，
B．存在一条直线， ，
C．存在两条平行直线，，，，，
D．存在两条异面直线，，，，，
2．（2022湖北省）已知a，b，c为三条不重合的直线，，，为三个不重合的平面其中正确的命题（ ）
①，；②，；③，；④，；
⑤，，．
A．①⑤B．①②C．②④D．③⑤
3．（2022天津）a，b，c为三条不重合的直线，，，为三个不重合的平面．给出下列四个命题：
①； ②
③； ④．
其中真命题是．
A．①②③B．①③C．①④D．①③④
考点六 距离相关问题
【例6】（2022山西）已知正方体的棱长为分别是棱的中点，动点在正方形（包括边界）内运动，若平面，则线段的长度范围是（ ）
A．B．
C．D．
【一隅三反】
1．（2023安徽）已知正方体的棱长为1，点是平面的中心，点是平面的对角线上一点，且平面，则线段的长为（ ）
A．B．C．D．
2（2022甘肃）在棱长为1的正方体ABCD﹣A1B1C1D1中，点M，N分别是棱BC，CC1的中点，动点P在正方形BCC1B1（包括边界）内运动．若平面AMN，则PA1的最小值是（ ）
A．1B．C．D．
3（2023黑龙江）已知正方体的棱长为分别是棱的中点，动点在正方形（包括边界）内运动，若面，则线段的长度范围是（ ）
A．B．C．D．
8.5 空间直线、平面的平行（精讲）
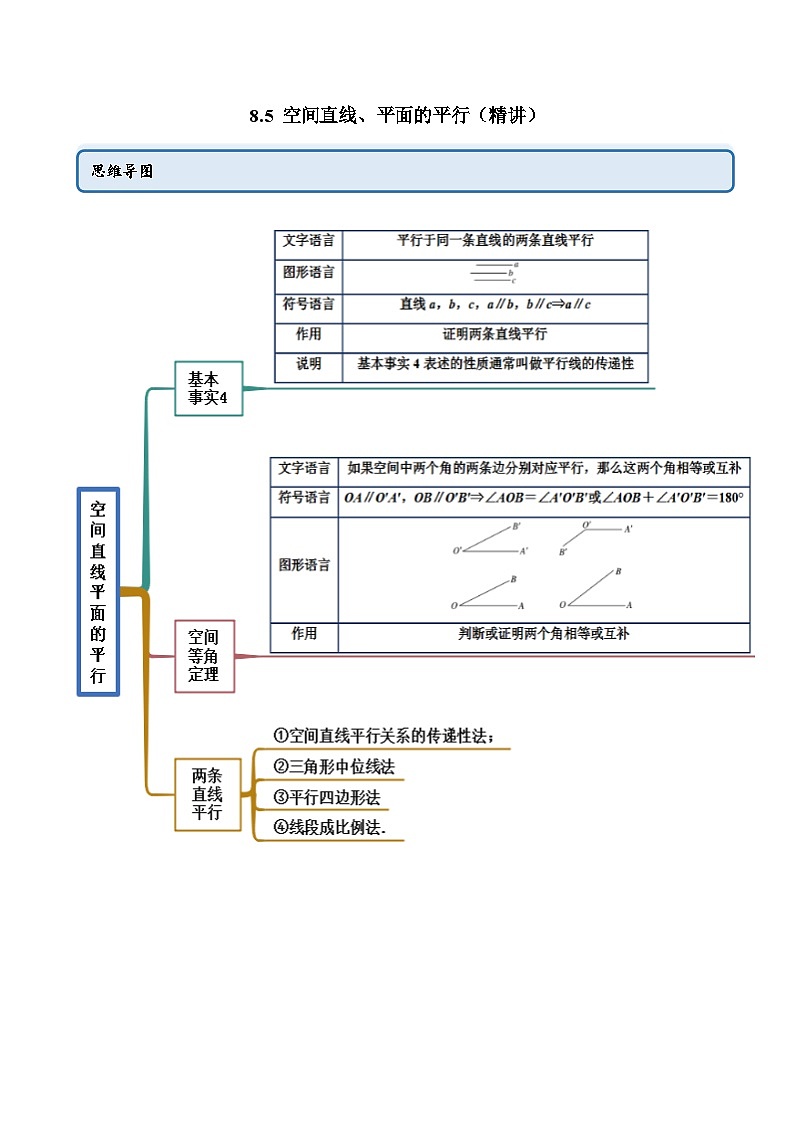
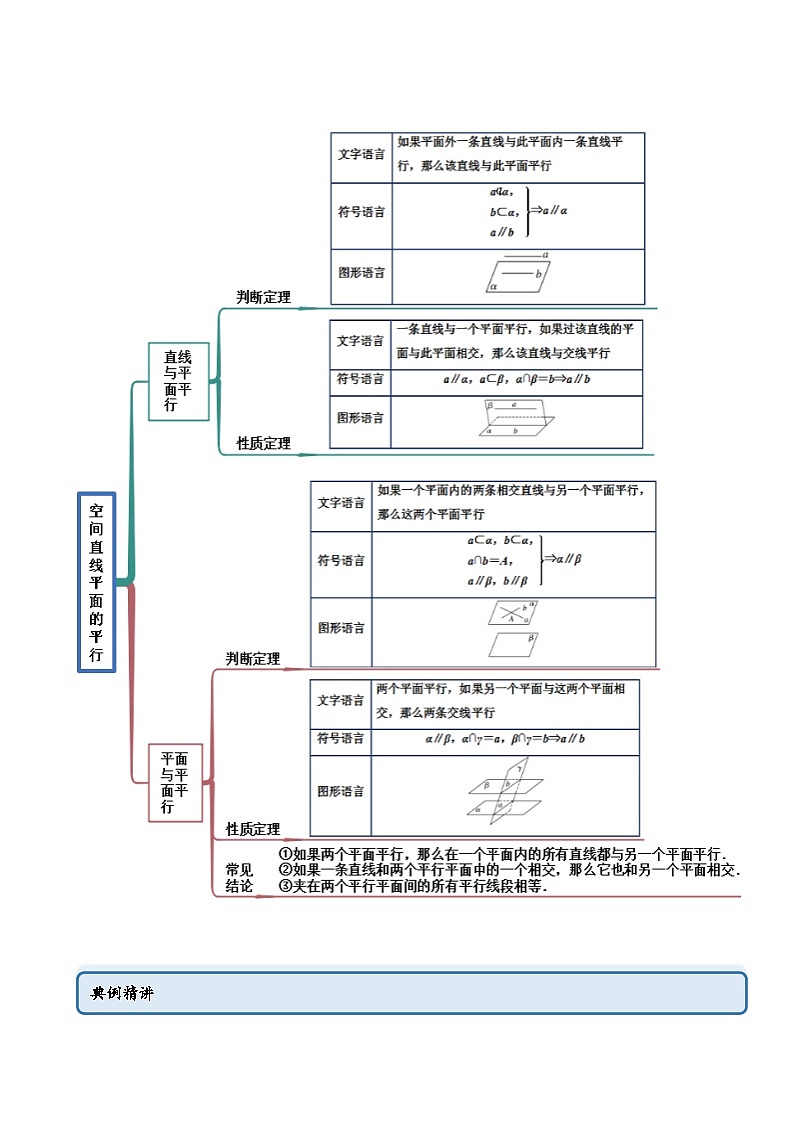
思维导图
典例精讲
考点一 线线平行
【例1-1】（2022广西）若，且，与方向相同，则下列结论正确的有（ ）
A．且方向相同B．，方向可能不同
C．OB与不平行D．OB与不一定平行
【答案】D
【解析】如图，
；
当∠AOB=∠A1O1B1时，且OA∥O1A1，OA与O1A1的方向相同，
OB与O1B1是不一定平行． 故选：D．
【例1-2】（2022云南）如图所示，在长方体AC1中，E，F分别是B1O和C1O的中点，则长方体的各棱中与EF平行的有（ ）
A．3条B．4条
C．5条D．6条
【答案】B
【解析】由于E，F分别是B1O，C1O的中点，故EF∥B1C1，
因为与棱B1C1平行的棱还有3条：AD, BC，A1D1，所以共有4条.故选：B.
【一隅三反】
1．（2022山东）如图，点P，Q，R，S分别在正方体的四条棱上，且是所在棱的中点，则直线PQ与RS是平行直线的图是________(填序号).
【答案】①②
【解析】根据正方体的结构特征，可得①②中RS与PQ均是平行直线，④中RS和PQ是相交直线，③中RS和PQ是是异面直线.故答案为：①②.
2（2022黑龙江）如图所示，在三棱柱中，，，，分别是，，，的中点，求证：,,,四点共面.
【答案】证明见解析
【解析】证明：∵G，H分别是A1B1，A1C1的中点，∴GH是A1B1C1的中位线，∴GHB1C1，
又∵B1C1BC，∴GHBC，∴B，C，H，G四点共面.
3．（2022甘肃）如图，E，F分别是长方体ABCD­A1B1C1D1的棱A1A，C1C的中点．求证：四边形B1EDF为平行四边形．
【答案】证明见解析
【解析】由于分别是长方体的中点，
设是的中点，连接，
根据长方体的性质可知且，
所以四边形是平行四边形.
考点二 等角性质
【例2-1】（2022北京）已知，，，则（ ）
A．B．或
C．D．或
【答案】B
【解析】的两边与的两边分别平行，根据等角定理易知或.
故选：B.
【例2-2】（2022广东省连平县）如图，在正方体中，，分别是棱和的中点．
（1）求证：四边形为平行四边形；
（2）求证：．
【答案】（1）证明见解析；（2）证明见解析.
【解析】(1)∵为正方体．∴，且，
又，分别为棱，的中点，∴且，
∴四边形为平行四边形，∴且．
又且，∴且，
∴四边形为平行四边形．
(2)法一：由(1)知四边形为平行四边形，∴．
同理可得四边形为平行四边形，∴．∵和方向相同，
∴．
法二：由(1)知四边形为平行四边形，∴．
同理可得四边形为平行四边形，∴．
又∵，∴，∴．
【一隅三反】
1．（2022湖南）下列结论，其中正确的是________(填序号).
①如果一个角的两边与另一个角的两边分别平行，那么这两个角相等.
②如果两个角的两边都平行于一个平面，那么这两角相等或互补.
③如果一个角的两边和另一个角的两边分别垂直，那么这两个角相等或互补.
④如果两条直线同时平行于第三条直线，那么这两条直线互相平行.
【答案】④
【解析】根据等角定理可知：
对于①：这两个角相等或互补，①错误；
对于②、③：无法判定这两个角的两边分别平行，所以无法确定这两角的大小关系，②、③错误；
对于④：根据平行线的传递性，④正确；
故答案为：④．
2．（2022浙江）如图，三棱柱中，，，分别为，，的中点.求证：.

【答案】证明见解析
【解析】证明：因为，分别是，的中点，所以，
所以四边形为平行四边形，所以.同理可证，
又与方向相同，所以.
3．（2022江苏）长方体中，分别为棱的中点.
（1）求证：；
（2）求证：.
【答案】（1）证明见解析；（2）证明见解析.
【解析】证明：（1）如图，取的中点，连接.
在矩形中，易得，
因为，，所以，
所以四边形为平行四边形，所以.
在矩形中，易得，.
所以四边形为平行四边形，所以，所以.
（2）因为，，又与的对应边方向相同，所以.
考点三 线面平行
【例3-1】（2022四川）如图，四棱锥中，底面为边长为2的菱形且对角线与交于点O，底面，点E是的中点．
(1)求证：∥平面；
(2)若三棱锥的体积为，求的长．
【答案】(1)证明见解析(2)
【解析】（1）证明：连接．
∵点O，E分别为的中点，∴，∵平面平面，∴∥平面；
（2）取中点F，连接．
∵E为中点，∴为的中位线，∴，且．由菱形的性质知，为边长为2的等边三角形．
又平面，∴平面，，点E是的中点，
∴，∴．
【例3-2】（2022河北）如图，在四棱柱中，底面ABCD是等腰梯形，，，，，E、、F分别为棱AD、、AB的中点．证明：直线平面．
【答案】证明见解析
【解析】证明：如图，取的中点，连接，，
因为，所以平面，
因此，平面即为平面．
连接，，因为，
所以四边形为平行四边形，
因此，又，所以，
而平面，平面，
故平面．
【例3-3】（2022山东省）如图，四棱锥的底面为平行四边形，分别为的中点.
(1)证明：AF平面；
(2)在线段上是否存在一点，使得平面，并给出必要的证明.
【答案】(1)证明见解析
(2)存在，证明见解析
【解析】（1）证明：取中点，连接，在中，为的中点，.
为的中点，，
即四边形为平行四边形，.
平面平面平面.
（2）设，取中点，连接，则在中，
分别是的中点，
平面平面，
平面.
与相似，且相似比为，
为的三等分点.
在点位置时满足平面.
即点在线段靠近端的三等分点时符合题意.
【一隅三反】
1．（2022吉林）在正方体中，分别是的中点，则下列说法中错误的是（ ）
A．平面B．平面
C．平面D．平面
【答案】C
【解析】如图所示，连接和相交于点O，则O为，的中点.
对于A，连接，则,因为平面，平面，
所以平面，故A正确；
对于B，易知,因为平面，平面，
所以平面，故B正确；
对于C，因为,所以与平面相交，故C错误；
对于D，易知,因为平面,平面，
所以平面，故D正确.
故选:C.
2．（2022上海）如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是（ ）
A．B．
C．D．
【答案】A
【解析】对于选项B，如图1，连接CD，
因为M，N，Q为所在棱的中点，所以CDMQ，
由于ABCD，所以ABMQ，
因为平面，平面，所以AB平面MNQ，
B选项不满足题意；
对于选项C，如图2，连接CD，
因为M，N，Q为所在棱的中点，所以CDMQ，
由于ABCD，所以ABMQ，
因为平面，平面，所以AB平面MNQ，
C选项不满足题意；
对于选项D，如图3，连接CD，
因为M，N，Q为所在棱的中点，所以CDNQ，
由于ABCD，所以ABNQ，
因为平面，平面，所以AB平面MNQ，
可知D不满足题意；
如图4，取BC的中点D，连接QD，
因为Q是AC的中点，
所以QDAB，
由于QD与平面MNQ相交，故AB与平面MNQ不平行，
A正确.
故选：A
3.（2022山东省）如图所示，正四棱锥P—ABCD的各棱长均为13，M为PA上的点，且PM∶MA=5∶8.
(1)在线段BD上是否存在一点N，使直线MN平面PBC？如果存在，求出BN∶ND的值，如果不存在，请说明理由；
(2)假设存在满足条件（1）的N点，求线段MN的长.
【答案】(1)存在，(2)7
【解析】（1）存在，；理由如下：
连接并延长，交于，连接.
因为正方形中，，所以;
又因为，所以；
平面，平面，所以平面.
（2）由（1）得，所以；
中，
，
所以；
因为，所以
所以.
4．（2022山东省）如图，在四棱锥中，底面为平行四边形，是上一点，当点满足条件：________时，平面.
【答案】答案表述不唯一)
【解析】连接交于O，连接OE，
平面平面，平面平面 ，
.
又 底面为平行四边形，为对角线与的交点，
故为的中点, 为的中点，
故当满足条件: 时，面.
故答案为: 答案表述不唯一)
考点四 面面平行
【例4-1】（2022陕西省）如图，在三棱柱中，分别为的中点，．求证：
(1)平面；
(2)平面平面．
【答案】(1)证明见解析(2)证明见解析
【解析】（1）在三棱柱中，分别为的中点，
，
平面平面，
平面．
（2）平面，平面，
平面．
分别为的中点，，
，且．
四边形是平行四边形．
．
又平面平面，
平面．
又平面，
平面平面．
【例4-2】．（2022海南）（多选）在正方体中，下列四组面中彼此平行的有（ ）
A．平面与平面B．平面与平面
C．平面与平面D．平面与平面
【答案】ABC
【解析】对于A选项，
，平面，平面，则平面，
同理可证，平面，
因为，平面，平面，
所以平面平面，故A正确；
对于B选项，
，平面，平面，则平面，
同理可证，平面，
因为，平面，平面，
所以平面平面，故B正确；
对于C选项，
，平面，平面，则平面，
同理可证，平面，
因为，平面，平面，
所以平面平面，故C正确；
对于D选项，
设，则平面且平面，
设，则平面且平面，
所以平面平面，故两个平面相交，故D错误.
故选：ABC.
【一隅三反】
1．（2022北京）如图，在长方体中，写出满足条件的一个平面：
（1）与平面平行的平面为______；
（2）与平面平行的平面为______；
（3）与平面平行的平面为______．
【答案】（1）平面 （2）平面 （3）平面
【解析】因为为长方体，所以平面∥平面，平面∥平面，同时∥，∥，
又因为平面，平面，所以∥面，∥平面，因为，所以平面∥平面.
故答案为：①平面；②平面；③平面.
2．（2022山东省）如图：在正方体中，为的中点.
(1)求证：平面；
(2)若为的中点，求证：平面平面.
【答案】(1)见解析(2)见解析
【解析】（1）证明：设，接，
在正方体中，四边形是正方形，是中点，
是的中点，，
平面平面
平面；
（2）证明：为的中点，为的中点，
，
四边形为平行四边形，，
又平面平面平面，
由（1）知平面平面平面，
平面平面.
3（2022山东省）由四棱柱截去三棱锥后得到的几何体如图所示，四边形为平行四边形，O为与的交点．
(1)求证：∥平面；
(2)求证：平面∥平面；
(3)设平面与底面的交线为l，求证：．
【答案】证明见解析
【解析】（1）取的中点，连接，
∵是四棱柱，∴，
∴四边形为平行四边形，∴，
又平面平面，∴平面．
（2）∵，∴四边形是平行四边形，∴，
∵平面平面，∴平面，
由（1）得平面且，平面，
∴平面平面．
（3）由（2）得：平面，
又平面，平面平面，∴．
考点五 判断定理与性质定理辨析
【例5-1】（2022广东）已知为不同的平面，a，b为不同的直线，那么下列条件中能推出与平行的是（ ）
A．内有无数条直线与平行B．
C．直线，且D．内任何直线都与平行
【答案】D
【解析】对于A，内有无数条直线与平行，则与相交或平行，故A错误；
对于B，若，则与相交或平行，故B错误；
对于C，若直线，且，则与相交或平行，故C错误；
对于D，若内任何直线都与平行，则与平行，故D正确.
故选：D.
【例5-2】（2022山东省）已知为三条不重合的直线，是两个不重合的平面，给出下列四个说法：
①，则；
②，则；
③，则；
④，则.
其中正确的是（ ）
A．①④B．①②C．②④D．③④
【答案】C
【解析】对①，，则，可以平行、相交或异面，故①不正确；
对②，根据平行线的传递性，可知②正确；
对③，，则或，故③不正确；
对④，根据线面平行的判定定理，可知④正确．
故选：C
【一隅三反】
1．（2022陕西省）下列条件中能推出平面平面的是（ ）
A．存在一条直线，，
B．存在一条直线， ，
C．存在两条平行直线，，，，，
D．存在两条异面直线，，，，，
【答案】D
【解析】A.如图所示：，存在一条直线，，，但平面与平面相交，故错误；
B.如图所示： ，存在一条直线，，，但平面与平面相交，故错误；
C. 如图所示：，存在两条平行直线，，，，，，但平面与平面相交，故错误；
D.如图所示：，在平面内过b上一点作，则，又，且，所以，故正确；
故选：D
2．（2022湖北省）已知a，b，c为三条不重合的直线，，，为三个不重合的平面其中正确的命题（ ）
①，；
②，；
③，；
④，；
⑤，，．
A．①⑤B．①②C．②④D．③⑤
【答案】A
【解析】①，，由平行公理4得，正确；
②，，则与有可能平行、相交、异面，故错误；
③，则或，故错误；
④，；则或，故错误；
⑤，，，由线面平行的判定定理可得．
故选：A.
3．（2022天津）a，b，c为三条不重合的直线，，，为三个不重合的平面．给出下列四个命题：
①； ②
③； ④．
其中真命题是．
A．①②③B．①③C．①④D．①③④
【答案】C
【解析】,所以①正确；
位置关系不定，所以②错误；
位置关系不定，所以③错误；
，所以④正确选C.
考点六 距离相关问题
【例6】（2022山西）已知正方体的棱长为分别是棱的中点，动点在正方形（包括边界）内运动，若平面，则线段的长度范围是（ ）
A．B．
C．D．
【答案】B
【解析】如图，分别作的中点,连接
显然,
且平面，；平面,
所以平面平面
平面平面
所以动点在正方形的轨迹为线段
在三角形中，，
所以点到点的最大距离为，最小距离为等腰三角形在边上的高为故选：B
【一隅三反】
1．（2023安徽）已知正方体的棱长为1，点是平面的中心，点是平面的对角线上一点，且平面，则线段的长为（ ）
A．B．C．D．
【答案】B
【解析】连接，，则过点.如图所示
∵平面，平面平面，平面，
∴，∵，
∴.
故选：B.
2（2022甘肃）在棱长为1的正方体ABCD﹣A1B1C1D1中，点M，N分别是棱BC，CC1的中点，动点P在正方形BCC1B1（包括边界）内运动．若平面AMN，则PA1的最小值是（ ）
A．1B．C．D．
【答案】C
【解析】
如图所示，取的中点,的中点，连接，
因为分别是棱 的中点，所以，，
又因为,,，
所以平面平面，平面，且点在右侧面，
所以点的轨迹是，且，，
所以当点位于中点处时，最小，
此时，.
故选：C
3（2023黑龙江）已知正方体的棱长为分别是棱的中点，动点在正方形（包括边界）内运动，若面，则线段的长度范围是（ ）
A．B．C．D．
【答案】D
【解析】由题意，取的中点，的中点，连接，，，，，
作图如下：
在正方体中，易知，，，
则共面，平面，平面，
平面，同理可得：平面，
，平面平面，
当平面时，平面，
正方体的棱长为，
在中，，解得，同理，
在中，，解得，
则中边上的高，
即，
故选：D.