高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直一课一练
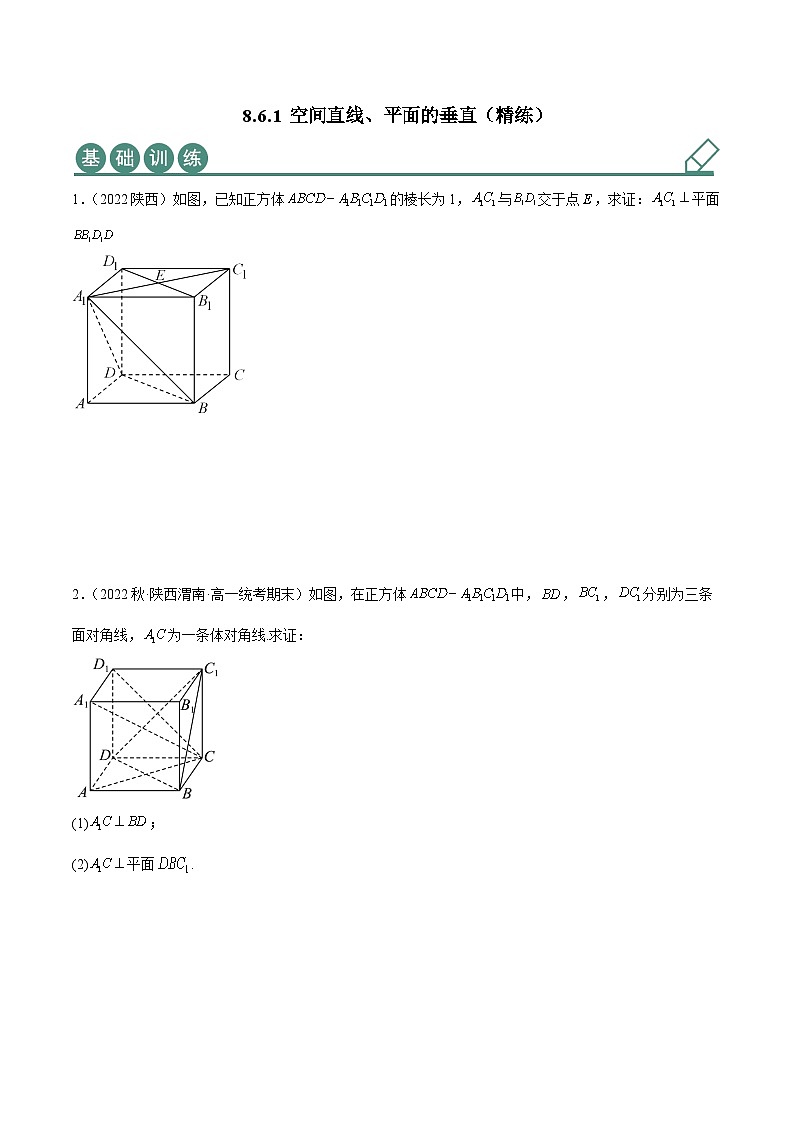
展开1.(2022陕西)如图,已知正方体的棱长为1,与交于点,求证:平面
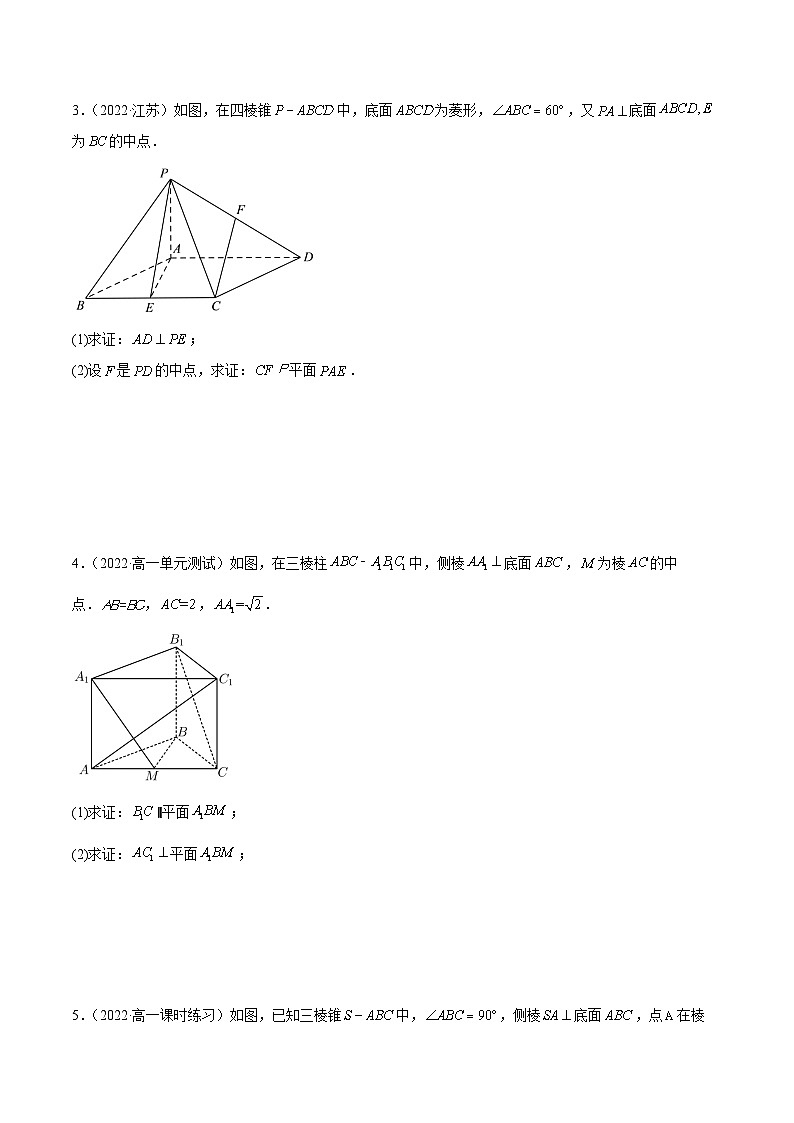
2.(2022秋·陕西渭南·高一统考期末)如图,在正方体中,,,分别为三条面对角线,为一条体对角线.求证:
(1);
(2)平面.
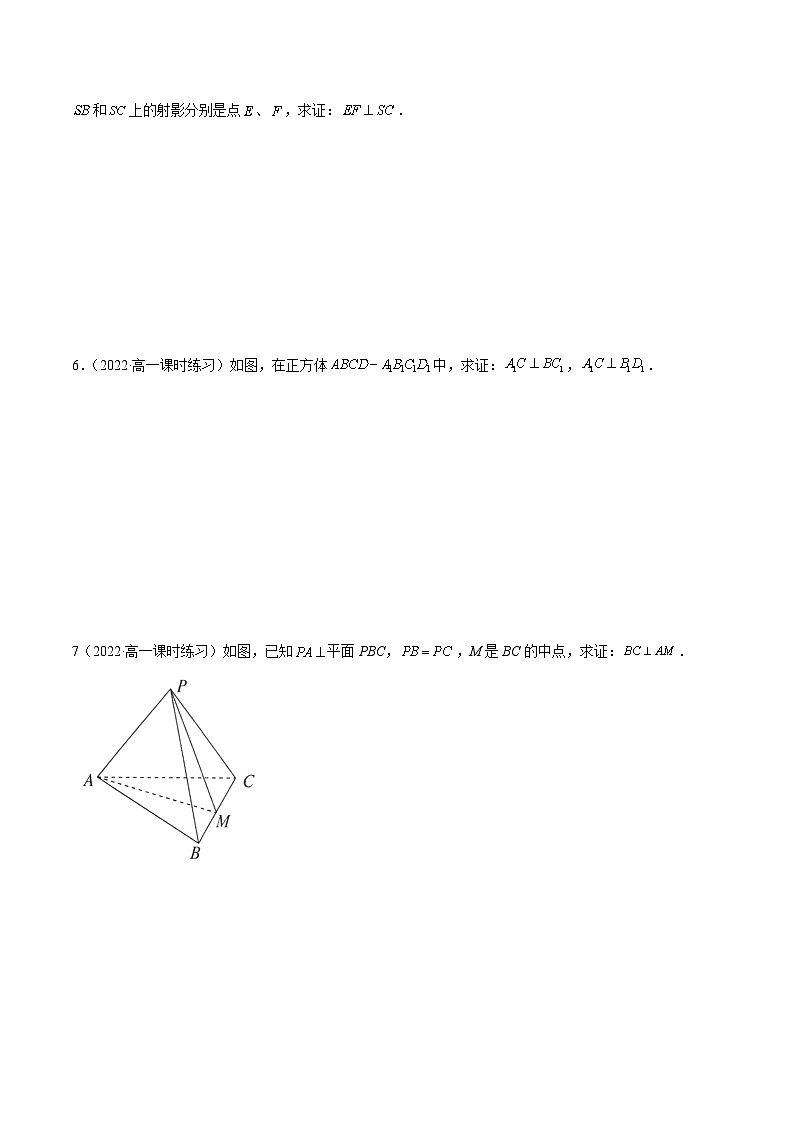
3.(2022·江苏)如图,在四棱锥中,底面为菱形,,又底面为的中点.
(1)求证:;
(2)设是的中点,求证:平面.
4.(2022·高一单元测试)如图,在三棱柱中,侧棱底面,为棱的中点.,,.
(1)求证:∥平面;
(2)求证:平面;
5.(2022·高一课时练习)如图,已知三棱锥中,,侧棱底面,点在棱和上的射影分别是点、,求证:.
6.(2022·高一课时练习)如图,在正方体中,求证:,.
7(2022·高一课时练习)如图,已知平面PBC,,M是BC的中点,求证:.
8.(2022·高一课时练习)在正三棱柱中,如图所示,,G,E,F分别是,AB,BC的中点,求证:直线直线GB.
9.(2022春·广东揭阳·高一统考期末)圆柱如图所示,为下底面圆的直径,为上底面圆的直径,底面,,,.
(1)证明:面.
(2)求圆柱的体积.
10.(2022·高一课时练习)在四棱锥PABCD中,PA⊥平面ABCD,四边形ABCD是矩形,AE⊥PD于点E,l⊥平面PCD.求证:l∥AE.
11.(2022·高一课时练习)如图,已知正方体A1C.
(1)求证:A1C⊥B1D1;
(2)M,N分别为B1D1与C1D上的点,且MN⊥B1D1,MN⊥C1D,求证:MN∥A1C.
12.(2021春·福建厦门·高一厦门双十中学校考期中)如图,在四棱锥P-ABCD中,∠ADB=90°,CB=CD,点E为棱PB的中点.
(1)若PB=PD,求证:PC⊥BD;
(2)求证:CE∥平面PAD.
13.(2022春·宁夏吴忠·高一青铜峡市高级中学校考期末)如图,已知四棱锥P-ABCD的底面ABCD是菱形,PA⊥平面ABCD,点E为PC的中点.
(1)求证:平面BDE;
(2)求证:PC⊥BD.
14(2022·全国·高一专题练习)如图所示,和所在平面互相垂直,且,点分别为的中点,求证:平面
15.(2022·高一单元测试)如图所示,M是菱形ABCD所在平面外一点,.求证:AC 垂直于平面BDM.
16.(2022·高一单元测试)如图,是正方形所在平面外一点,,且平面平面,,分别是线段,的中点.
(1)求证:
(2)求证:平面
17.(2021秋·陕西渭南·高一校考阶段练习)如图,在三棱柱中,底面是中点,与相交于点.
(1)证明: 平面;
(2)若四边形是正方形,,求证:平面平面.
18.(2022春·福建泉州·高一校考期中)如图,在四棱锥中,底面,底面是正方形.
(1)证明: 平面;
(2)证明:平面平面.
19.(2022·高一单元测试)如图所示,在矩形中,,为的中点.将沿折起,使得平面平面.点是线段的中点.
(1)求证:平面平面;
(2)求证:
20.(2022春·云南文山·高一统考期末)如图,在四棱锥中,底面为直角梯形,,平面底面分别为的中点..
(1)求证:直线平面;
(2)求三棱锥的体积.
1(2021秋·河南安阳·高一安阳一中校考期末)如图所示,平面四边形ABCD中,AB=AD,AB⊥AD,BD⊥CD,将其沿对角线BD折成四面体A-BCD,使平面ABD⊥平面BCD,则下列说法中正确的是( )
①平面ACD⊥平面ABD;②AB⊥AC;③平面ABC⊥平面ACD.
A.①②B.②③
C.①③D.①②③
2.(2022春·贵州六盘水·高一校考阶段练习)在四棱锥中,已知底面,且底面为矩形,则下列结论中错误的是( )
A.平面平面B.平面平面
C.平面平面D.平面平面
3.(2022黑龙江)(多选)如图,在三棱锥P-ABC中,平面的中点,则下列结论正确的是( )
A.平面 B. C.平面 D.平面
4.(2021秋·河北沧州·高三沧县中学校考阶段练习)(多选)设m、n、l表示不同的直线,表示不同的平面,则下列命题中正确的是( )
A.,则B.,则
C.,则D.,则
5(2023·江苏)如图,在直角梯形中,,,,并将直角梯形绕AB边旋转至ABEF.
(1)求证:直线平面ADF;
(2)求证:直线平面ADF;
(3)当平面平面ABEF时,再从条件①、条件②、条件③这三个条件中选择一个作为已知,使平面ADE与平面BCE垂直.并证明你的结论.
条件①:;
条件②:;
条件③:.
6.(2022春·河南开封·高一统考期中)在条件①;②;③平面平面中任选一个,补充到下面的问题中,并给出问题解答.
问题:如图,在直三棱柱中,,且________,求证:.
7(2022辽宁)如图,在中,,,.分别是上的点,且,将沿折起到的位置,使,如图.
(1)求证:平面;
(2)求证:平面;
(3)当点在何处时,的长度最小,并求出最小值.
8.(2022·高一单元测试)如图,直三棱柱的体积为4,的面积为.
(1)求到平面的距离;
(2)设D为的中点,,平面平面,求线段BC的长度.
9.(2022春·重庆铜梁·高一统考期末)如图,在四棱锥中,四边形是等腰梯形,,,.点为棱的中点,点为棱上的一点,且,平面平面.
(1)证明:;
(2)证明:平面.
8.6.1 空间直线、平面的垂直(精练)
1.(2022陕西)如图,已知正方体的棱长为1,与交于点,求证:平面
【答案】证明见解析
【解析】因为四边形为正方形,.
在正方体中,易知平面,
又平面,.
又,平面,
平面.
2.(2022秋·陕西渭南·高一统考期末)如图,在正方体中,,,分别为三条面对角线,为一条体对角线.求证:
(1);
(2)平面.
【答案】(1)证明见解析
(2)证明见解析
【解析】(1)在正方体中,平面,
∵平面,∴,
又四边形为正方形,∴,
又,平面,∴平面,
又平面,∴.
(2)与(1)中证明同理可证,又,平面
∴平面.
3.(2022·江苏)如图,在四棱锥中,底面为菱形,,又底面为的中点.
(1)求证:;
(2)设是的中点,求证:平面.
【答案】(1)答案见解析(2)答案见解析
【解析】(1)因为底面为菱形,,且为的中点,所以.
又,所以.
又底面底面,所以.
因为平面平面,所以平面,
平面,所以.
(2)取的中点,连接,
是中点,,,
,平面,平面,平面,
,平面,平面,平面,
又平面平面,
平面平面,
平面,平面.
4.(2022·高一单元测试)如图,在三棱柱中,侧棱底面,为棱的中点.,,.
(1)求证:∥平面;
(2)求证:平面;
【答案】(1)证明见解析(2)证明见解析
【解析】(1)连接与,两线交于点,连接.
在中,∵,分别为,的中点,∴,
又∵平面,平面,∴平面.
(2)∵侧棱底面,平面,∴,
又∵为棱的中点,,∴.
∵,,平面,∴平面,
又平面,∴
∵,∴.又∵,
∴在和中,,
∴,
即,∴
∵,,平面,∴平面.
5.(2022·高一课时练习)如图,已知三棱锥中,,侧棱底面,点在棱和上的射影分别是点、,求证:.
【答案】证明见解析
【解析】由题意,平面,平面,故.
又,,平面,则平面
又平面,故,又,,平面,故平面.
又平面,故,又,,平面,故平面.
因为平面,故,即得证.
6.(2022·高一课时练习)如图,在正方体中,求证:,.
【答案】证明见解析
【解析】如图,在正方体中,平面,平面,∴,
又,,平面,∴平面,
∵平面,∴;
同理,平面,平面,∴,
又,,平面,∴平面,
∵平面,∴.
7(2022·高一课时练习)如图,已知平面PBC,,M是BC的中点,求证:.
【答案】证明见解析.
【解析】∵,M是BC的中点,
∴.
又平面PBC,平面PBC,则,
∵,面,
∴面,而面,
∴.
8.(2022·高一课时练习)在正三棱柱中,如图所示,,G,E,F分别是,AB,BC的中点,求证:直线直线GB.
【答案】证明见解析
【解析】证明:连接.在三角形中,G是的中点,所以.
因为平面,平面,
所以,
因为,平面,
所以⊥平面,
因为平面,
所以⊥,
又因为E,F分别是AB,BC的中点,所以,所以
所以直线直线GB.
9.(2022春·广东揭阳·高一统考期末)圆柱如图所示,为下底面圆的直径,为上底面圆的直径,底面,,,.
(1)证明:面.
(2)求圆柱的体积.
【答案】(1)见解析
(2)
【解析】(1)
证明:连接,,,
可得平面,
∵平面,
∴,
∵,
∴四边形为平行四边形,
∴,
∴且,
∴四边形为平行四边形,
∴,
∵平面,平面,
∴平面;
(2)
解:连接,
∵,∴,
∵垂直上底面,∴,
∵,平面,,
∴平面,
又平面,
∴,
∵,∴,
∴为等腰直角三角形,,
∴圆柱的体积为.
10.(2022·高一课时练习)在四棱锥PABCD中,PA⊥平面ABCD,四边形ABCD是矩形,AE⊥PD于点E,l⊥平面PCD.求证:l∥AE.
【答案】证明见解析
【解析】证明:因为PA⊥平面ABCD,
CD⊂平面ABCD,
所以PA⊥CD.
又四边形ABCD是矩形,所以CD⊥AD.
因为PA∩AD=A,PA⊂平面PAD,AD⊂平面PAD,
所以CD⊥平面PAD.
又AE⊂平面PAD,所以AE⊥DC.
因为AE⊥PD,PD∩CD=D,PD⊂平面PCD,CD⊂平面PCD,
所以AE⊥平面PCD.
因为l⊥平面PCD,
所以l∥AE.
11.(2022·高一课时练习)如图,已知正方体A1C.
(1)求证:A1C⊥B1D1;
(2)M,N分别为B1D1与C1D上的点,且MN⊥B1D1,MN⊥C1D,求证:MN∥A1C.
【答案】(1)证明见解析
(2)证明见解析
【解析】(1)如下图,连接A1C1.
因为CC1⊥平面A1B1C1D1,B1D1⊂平面A1B1C1D1,
所以CC1⊥B1D1.因为四边形A1B1C1D1是正方形,
所以A1C1⊥B1D1.又因为CC1∩A1C1=C1,
所以B1D1⊥平面A1C1C.又因为A1C⊂平面A1C1C,所以B1D1⊥A1C.
(2)如上图,连接B1A,AD1.因为B1C1= AD,B1C1∥ AD
所以四边形ADC1B1为平行四边形,所以C1D∥AB1,因为MN⊥C1D,所以MN⊥AB1.
又因为MN⊥B1D1,AB1∩B1D1=B1,所以MN⊥平面AB1D1.由(1)知A1C⊥B1D1.
同理可得A1C⊥AB1.又因为AB1∩B1D1=B1,所以A1C⊥平面AB1D1.所以A1C∥MN.
故答案为:A1C⊥B1D1;MN∥A1C.
12.(2021春·福建厦门·高一厦门双十中学校考期中)如图,在四棱锥P-ABCD中,∠ADB=90°,CB=CD,点E为棱PB的中点.
(1)若PB=PD,求证:PC⊥BD;
(2)求证:CE∥平面PAD.
【答案】(1)证明见解析;(2)证明见解析.
【解析】(1)取BD的中点O,连接CO,PO,
因为CD=CB,
所以△CBD为等腰三角形,
所以BD⊥CO
因为PB=PD,
所以△PBD为等腰三角形,所以BD⊥PO
又PO∩CO=O,PO,CO⊂平面PCO,
所以BD⊥平面PCO
因为PC⊂平面PCO,所以PC⊥BD;
(2)由E为PB的中点,连接EO,则EO∥PD,
又EO⊄平面PAD,PD⊂平面PAD,
所以EO∥平面PAD.
由∠ADB=90°及BD⊥CO,可得CO∥AD,
又CO⊄平面PAD,AD⊂平面PAD,
所以CO∥平面PAD.
又CO∩EO=O,CO,EO⊂平面COE,
所以平面CEO∥平面PAD,
而CE⊂平面CEO,所以CE∥平面PAD.
13.(2022春·宁夏吴忠·高一青铜峡市高级中学校考期末)如图,已知四棱锥P-ABCD的底面ABCD是菱形,PA⊥平面ABCD,点E为PC的中点.
(1)求证:平面BDE;
(2)求证:PC⊥BD.
【答案】(1)证明见解析(2)证明见解析
【解析】(1)证明:连接AC交BD于O点,连接EO,
如图所示:
∵底面ABCD是菱形,∴O为AC的中点
∵点E为PC的中点,∴
∵平面BDE,且平面BDE
∴平面BDE
(2)证明:∵底面ABCD是菱形,∴AC⊥BD,
∵PA⊥平面ABCD,底面ABCD,
∴PA⊥BD
∵,平面PAC,
∴BD⊥平面PAC,又平面PAC,
∴BD⊥PC.
14(2022·全国·高一专题练习)如图所示,和所在平面互相垂直,且,点分别为的中点,求证:平面
【答案】证明见解析
【解析】证明:由且,
可得,所以,
又由为的中点,所以,
因为为的中点,同理可得,
又因为且平面,所以平面,
因为分别为的中点,所以,所以平面.
15.(2022·高一单元测试)如图所示,M是菱形ABCD所在平面外一点,.求证:AC 垂直于平面BDM.
【答案】证明见解析.
【解析】设AC交BD于点O,连接MO,
因为 ABCD 是菱形,所以,
因为,且,
所以,
因为MO、BD 是平面 BDM 上的两条相交直线,
所以 AC 垂直于平面 BDM.
16.(2022·高一单元测试)如图,是正方形所在平面外一点,,且平面平面,,分别是线段,的中点.
(1)求证:
(2)求证:平面
【答案】(1)证明见解析(2)证明见解析
【解析】(1)因为正方形,
又平面平面
平面平面,
平面,
所以平面,
因为平面,
所以.
(2)
取中点,连接,,
在中,因为,分别是,的中点,
所以,
因为是正方形边中点,
所以,
所以,
即四边形是平行四边形,
所以,
又因为平面,平面,
故EF平面
17.(2021秋·陕西渭南·高一校考阶段练习)如图,在三棱柱中,底面是中点,与相交于点.
(1)证明: 平面;
(2)若四边形是正方形,,求证:平面平面.
【答案】(1)证明见解析(2)证明见解析
【解析】(1)易知分别为的中点,
是的中位线, ,
平面平面,
平面;
(2)底面 平面,
又平面,且,
平面,
又 平面,
四边形是正方形,,
平面,
平面,
又平面平面平面.
18.(2022春·福建泉州·高一校考期中)如图,在四棱锥中,底面,底面是正方形.
(1)证明: 平面;
(2)证明:平面平面.
【答案】(1)证明见解析;
(2)证明见解析;
【解析】(1)因为底面是正方形,所以.
又因为平面,平面,
所以平面.
(2)因为底面是正方形,所以.
因为 底面,在平面内,所以 .
又,、在平面内,所以平面.
又因为平面,
所以平面平面.
19.(2022·高一单元测试)如图所示,在矩形中,,为的中点.将沿折起,使得平面平面.点是线段的中点.
(1)求证:平面平面;
(2)求证:
【答案】(1)证明见解析
(2)证明见解析
【解析】(1)证明:在矩形中,,为的中点,∴,是的中点,∴,
∵平面平面,平面平面,平面,
平面,∴平面平面;
(2)证明:在矩形中,,为的中点,∴,则,∴,
由(1)知,平面,∵平面,∴,
∵,平面,平面,∴平面,
又∵平面,∴.
20.(2022春·云南文山·高一统考期末)如图,在四棱锥中,底面为直角梯形,,平面底面分别为的中点..
(1)求证:直线平面;
(2)求三棱锥的体积.
【答案】(1)证明见解析(2)
【解析】(1)因为为的中点,,所以,
又因为,所以四边形为平行四边形,
因为,所以平行四边形是矩形,所以,
因为,所以,
又因为平面平面,平面平面平面,
所以平面,因为平面,所以,
又因为平面,所以平面.
(2)因为,
所以,
由平面为中点,所以点到平面的距离等于,
所以.
1(2021秋·河南安阳·高一安阳一中校考期末)如图所示,平面四边形ABCD中,AB=AD,AB⊥AD,BD⊥CD,将其沿对角线BD折成四面体A-BCD,使平面ABD⊥平面BCD,则下列说法中正确的是( )
①平面ACD⊥平面ABD;②AB⊥AC;③平面ABC⊥平面ACD.
A.①②B.②③
C.①③D.①②③
【答案】D
【解析】∵平面平面BCD,平面平面,,CD平面BCD,
∴平面ABD,又∵CD平面ACD,
∴平面平面ABD,故①正确;
∵平面平面ABD,平面平面,,AB平面ABD,
∴平面ACD,∵AC平面ACD,∴,故②正确;
∵平面ACD,AB平面ABC,∴平面平面ACD,故③正确;
故选:D
2.(2022春·贵州六盘水·高一校考阶段练习)在四棱锥中,已知底面,且底面为矩形,则下列结论中错误的是( )
A.平面平面B.平面平面
C.平面平面D.平面平面
【答案】D
【解析】对于A中,由已知底面,且底面为矩形,
所以,且,平面,
所以平面,又由平面,所以平面平面,所以A正确;
对于B中,由已知底面,且底面为矩形,
所以,且,平面,
所以平面,又由平面,所以平面平面,所以B正确;
对于C中,由已知底面,且底面为矩形,
所以,且,平面,
所以平面,又由平面,所以平面平面,
所以C正确;
对于D中,设为平面与平面的交线,因为,平面,
平面,所以平面,因为为平面与平面的交线,
所以,又,所以,因为平面,平面,
所以,所以,又底面,所以,所以,
所以为平面与平面的二面角,若平面平面,
则,而底面,所以,此时三角形内角和大于,所以平面与平面不垂直,所以D错误.
故选:D.
3.(2022黑龙江)(多选)如图,在三棱锥P-ABC中,平面的中点,则下列结论正确的是( )
A.平面 B. C.平面 D.平面
【答案】ABC
【解析】平面,平面
,又,平面且
平面,故A正确
由平面,平面
得
又,是的中点,
又平面,
平面,平面
,故B,C正确
由平面,平面
得
因为与不平行
因此与不垂直
从而不与平面垂直,故D错误
故选:ABC.
4.(2021秋·河北沧州·高三沧县中学校考阶段练习)(多选)设m、n、l表示不同的直线,表示不同的平面,则下列命题中正确的是( )
A.,则B.,则
C.,则D.,则
【答案】ACD
【解析】选项A,根据空间中直线平行的传递性,可知A正确;
选项B,若,则m与l可能相交,也可能异面,也可能平行,故B错;
选项C,根据空间中平面平行的传递性,可知C正确;
选项D,两条平行线中的一条与一个平面垂直,则另一条也与这个平面垂直,故D正确;
故选:ACD.
5(2023·江苏)如图,在直角梯形中,,,,并将直角梯形绕AB边旋转至ABEF.
(1)求证:直线平面ADF;
(2)求证:直线平面ADF;
(3)当平面平面ABEF时,再从条件①、条件②、条件③这三个条件中选择一个作为已知,使平面ADE与平面BCE垂直.并证明你的结论.
条件①:;
条件②:;
条件③:.
【答案】(1)证明见解析(2)证明见解析(3)答案见解析
【解析】(1)证明:在直角梯形中,,,将直角梯形绕边旋转至,
所以,
又,平面,
所以平面;
(2)
证明:依题意可得且,
所以四边形为平行四边形,
所以,平面,平面,
所以平面;
(3)
证明:因为平面平面,,平面平面,平面,
所以平面,平面,所以,
过点作,交于点,
若选①,,,所以,
所以,此时,
所以
如图过点作交的延长线于点,
因为平面,平面,所以,
,平面,所以平面,
又平面,
所以平面平面,显然平面与平面不垂直;
若选②:,则,所以,,
所以,即,
又,平面,所以平面,
又平面,
所以平面平面;
若选③:,又,,平面,所以平面,
又平面,
所以平面平面;
6.(2022春·河南开封·高一统考期中)在条件①;②;③平面平面中任选一个,补充到下面的问题中,并给出问题解答.
问题:如图,在直三棱柱中,,且________,求证:.
【答案】证明见解析
【解析】(情况一)补充条件①.
证明:在直棱柱中,平面,
因为平面,所以.
因为,平面,平面
所以平面.
因为平面,所以,
因为,所以四边形为菱形,所以.
因为,平面,平面
所以平面.
因为平面,所以.
(情况二)补充条件②.
证明:设,连接.
因为,M为的中点,所以.
因为,所以四边形为菱形,所以.
因为平面平面,
所以平面.
因为平面,所以,
(情况三)补充条件③平面平面.
证明:在棱柱中,
因为,所以四边形为菱形,所以.
因为平面平面,平面平面平面,
所以平面.
因为平面,所以.
7(2022辽宁)如图,在中,,,.分别是上的点,且,将沿折起到的位置,使,如图.
(1)求证:平面;
(2)求证:平面;
(3)当点在何处时,的长度最小,并求出最小值.
【答案】(1)证明见解析
(2)证明见解析
(3)当为中点时,的长度最小,最小值为
【解析】(1),平面,平面,平面.
(2),,,,又,,
,,平面,平面.
(3)设,则,
由(2)知:均为直角三角形.
,
即,
当时,取得最小值;
当为中点时,的长度最小,最小值为.
8.(2022·高一单元测试)如图,直三棱柱的体积为4,的面积为.
(1)求到平面的距离;
(2)设D为的中点,,平面平面,求线段BC的长度.
【答案】(1)到平面的距离为
(2)线段BC的长为2
【解析】(1)解:由直三棱柱的体积为4,可得,
设到平面的距离为,由,
,,解得.
即到平面的距离为;
(2)解:连接交于点
由直三棱柱,
故四边形为正方形,,
又平面平面,平面平面,
平面,,
由直三棱柱知平面,
,又,
平面,,
,,又,
解得,
则线段BC的长为2.
9.(2022春·重庆铜梁·高一统考期末)如图,在四棱锥中,四边形是等腰梯形,,,.点为棱的中点,点为棱上的一点,且,平面平面.
(1)证明:;
(2)证明:平面.
【答案】(1)证明见解析
(2)证明见解析
【解析】(1)
证明:因为四边形为等腰梯形,则,
因为,则,所以,,故,
,即,
平面平面,平面平面,平面,
平面,
平面,.
(2)
证明:取的中点,连接,取的中点,连接、,
因为,,则,,
因为,且为的中点,所以,且,
因为,为的中点,所以,且,
所以,四边形为平行四边形,,
平面,平面,平面,
、分别为、的中点,故,
平面,平面,平面.
,、平面,平面平面,
平面,平面.
必修 第二册8.6 空间直线、平面的垂直一课一练: 这是一份必修 第二册<a href="/sx/tb_c4000306_t7/?tag_id=28" target="_blank">8.6 空间直线、平面的垂直一课一练</a>,共25页。试卷主要包含了线面垂直,面面垂直,线线垂直,判断与性质定理的辨析等内容,欢迎下载使用。
人教A版 (2019)必修 第二册第八章 立体几何初步8.5 空间直线、平面的平行同步达标检测题: 这是一份人教A版 (2019)必修 第二册<a href="/sx/tb_c4000305_t7/?tag_id=28" target="_blank">第八章 立体几何初步8.5 空间直线、平面的平行同步达标检测题</a>,共42页。试卷主要包含了线线平行,等角性质,线面平行,面面平行,判断定理与性质定理辨析,距离相关问题等内容,欢迎下载使用。
人教A版 (2019)必修 第二册8.5 空间直线、平面的平行达标测试: 这是一份人教A版 (2019)必修 第二册<a href="/sx/tb_c4000305_t7/?tag_id=28" target="_blank">8.5 空间直线、平面的平行达标测试</a>,共38页。













