

所属成套资源:高三数学一轮复习五层训练(新高考地区)(原卷版+解析)
高三数学一轮复习五层训练(新高考地区)第9练指数与指数函数(原卷版+解析)
展开
这是一份高三数学一轮复习五层训练(新高考地区)第9练指数与指数函数(原卷版+解析),共23页。试卷主要包含了课本变式练,考点分类练,最新模拟练,高考真题练,综合提升练等内容,欢迎下载使用。
1.(人A必修一P109习题4.1T7变式)设,则( )
A.4B.3C.2D.1
2.(人A必修一P118习题4.2T6变式)设,,,则( )
A.B.
C.D.
3. (人A必修一P109习题4.1T6变式)某食品的保鲜时间(单位:小时)与储藏温度(单位:)满足函数关系(为自然对数的底数,,为常数).若该食品在的保鲜时间是144小时,在的保鲜时间是36小时,则该食品在的保鲜时间是 小时
4. (人A必修一P118习题4.2T1变式)函数的定义域为 ;值域为 .
二、考点分类练
(一)指数幂的运算
5.(2022届河南省许平汝联盟高三下学期3月质量检测)已知,,则ab=( )
A.2B.C.D.1
6. (2022届“皖豫名校联盟体”高三第三次考试)某高山地区的大气压强p(Pa)与海拔高度h(m)近似满足函数关系,其中,是海平面大气压强,已知在该地区甲、乙两处测得的大气压强分别为,,且,那么甲、乙两处的海拔高度之差约为( )
(参考数据:)
A.4900mB.5500mC.6200mD.7400m
7. (多选)下列运算法则正确的是( )
A.
B.
C.(且)
D.
(二)指数函数的图象及应用
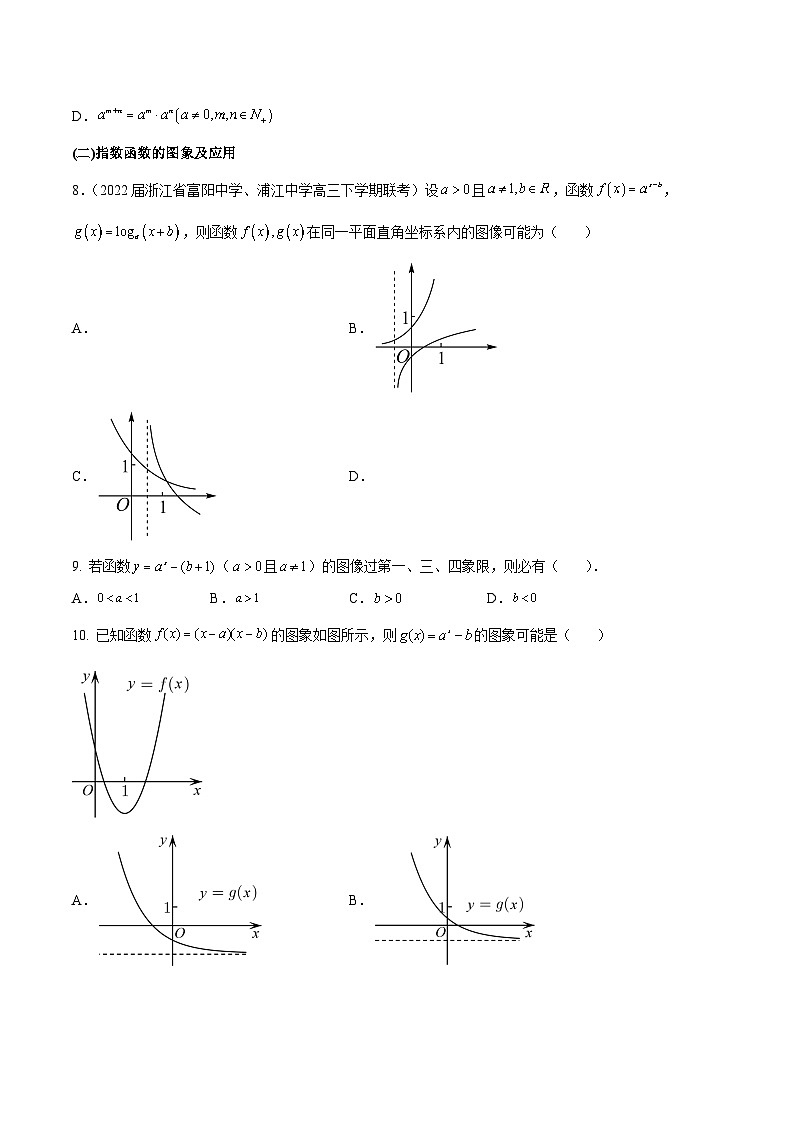
8.(2022届浙江省富阳中学、浦江中学高三下学期联考)设且,函数,,则函数在同一平面直角坐标系内的图像可能为( )
A.B.
C.D.
9. 若函数(且)的图像过第一、三、四象限,则必有( ).
A.B.C.D.
10. 已知函数的图象如图所示,则的图象可能是( )
A.B.
C.D.
(三)指数函数的性质及应用
11.(2022届广东省广州市高三上学期第三次月考)已知,则( )
A.B.
C.D.
12. (2022届山东省潍坊市高三上学期期末)已知函数,则下列结论中正确的是( )
A.的定义域为R
B.是奇函数
C.在定义域上是减函数
D.无最小值,无最大值
13. (2021届江西省南昌县高三上学期期末)已知,函数的零点分别为,函数的零点分别为,则的最小值为________.
三、最新模拟练
14.(2022届北京市西城区高三二模)若函数的定义域和值域的交集为空集,则正数的取值范围是( )
A.B.
C.D.
15.(2022届河南省豫西名校高三4月质检)若,则,,的大小关系为( )
A.B.
C.D.
16.(2022届安徽省合肥市高三下学期第二次教学质量检测)函数(是自然对数的底数)的图象关于( )
17.(2022届山西省晋中市高三二模)函数的图象大致是( )
A.B.
C.D.
18.(多选)(2022届广东省汕头市高三二模)设a,b,c都是正数,且,则下列结论正确的是( )
A.B.C.D.
19.(2022届河北省邯郸市大名县高三上学期强化训练)函数的图像恒过一定点,这个定点是___________.
20.(2022届江苏省南通市高三下学期联考)若,则的最小值为_________.
21.(2022届山西省吕梁市名校金科大联考高三上学期12月月考)已知函数(其中e是自然对数的底数).过点的直线与函数的图象交于,两点.
(1)若存在直线,使得,求的取值范围;
(2)证明:.
四、高考真题练
22.(2020全国卷Ⅰ)若,则( )
A.B.C.D.
23. (2020全国卷Ⅱ)若,则( )
A.B.C.D.
24.(2019全国卷Ⅲ)设是定义域为的偶函数,且在单调递减,则( )
A.B.
C.D.
25.(2017全国卷Ⅰ)设为正数,且,则( )
A.B.C.D.
26.(2016全国卷Ⅲ)已知,,,则( )
A.B.C.D.
五、综合提升练
27.(2022届上海市向明中学高三上学期月考)已知函数,设()为实数,且.给出下列结论:
①若,则;
②若,则.
其中正确的是( )
A.①与②均正确B.①正确,②不正确
C.①不正确,②正确D.①与②均不正确
28.(多选)(2022届江苏省盐城 、淮安、 宿迁 、如东等地高三上学期联考)已知函数,,若,则( )
A.
B.
C.
D.
29.(2022届陕西省西安市高三上学期练习)设函数和,若两函数在区间上的单调性相同,则把区间叫做的“稳定区间”.已知区间为函数的“稳定区间”,则实数的取值范围是___________
30.定义在D上的函数,如果满足:对任意,存在常数,都有成立,则称是D上的有界函数,其中称为函数的上界.
已知函数,.
(1)当时,求函数在上的值域,并判断函数在上是否为有界函数,请说明理由;
(2)若函数在上是以3为上界的有界函数,求实数a的取值范围;
(3)若,函数在上的上界是,求的取值范围.
第9练 指数与指数函数
一、课本变式练
1.(人A必修一P109习题4.1T7变式)设,则( )
A.4B.3C.2D.1
【答案】C
【解析】因为,所以,故.
故选C
2.(人A必修一P118习题4.2T6变式)设,,,则( )
A.B.
C.D.
【答案】D
【解析】,,,根据在上是增函数,所以,即.故选D.
3. (人A必修一P109习题4.1T6变式)某食品的保鲜时间(单位:小时)与储藏温度(单位:)满足函数关系(为自然对数的底数,,为常数).若该食品在的保鲜时间是144小时,在的保鲜时间是36小时,则该食品在的保鲜时间是 小时
【答案】18
【解析】,食品在的保鲜时间是144小时,在的保鲜时间是36小时,
,解得,即,,即该食品在的保鲜时间是18小时.
4. (人A必修一P118习题4.2T1变式)函数的定义域为 ;值域为 .
【答案】
【解析】由得的定义域为;由,得.
二、考点分类练
(一)指数幂的运算
5.(2022届河南省许平汝联盟高三下学期3月质量检测)已知,,则ab=( )
A.2B.C.D.1
【答案】B
【解析】因,,因此有,即,而函数在R上单调递增,则,
所以.故选B
6. (2022届“皖豫名校联盟体”高三第三次考试)某高山地区的大气压强p(Pa)与海拔高度h(m)近似满足函数关系,其中,是海平面大气压强,已知在该地区甲、乙两处测得的大气压强分别为,,且,那么甲、乙两处的海拔高度之差约为( )
(参考数据:)
A.4900mB.5500mC.6200mD.7400m
【答案】B
【解析】记甲、乙两处的海拔高度分别为,则由题可知:,则m,故选B
7. (多选)下列运算法则正确的是( )
A.
B.
C.(且)
D.
【答案】CD
【解析】对于A选项,若,则无意义,A选项错误;对于B选项,若,,则无意义,B选项错误;对于C选项,由换底公式可得(且),C选项正确;
对于D选项,当,、时,,D选项正确.故选CD.
(二)指数函数的图象及应用
8.(2022届浙江省富阳中学、浦江中学高三下学期联考)设且,函数,,则函数在同一平面直角坐标系内的图像可能为( )
A.B.
C.D.
【答案】B
【解析】函数,单调性相同,同增或者同减,故A错.
①若,,在定义域内单调递减,,令时,
如图C,若,则,此时的渐近线为,由图,解得,但此时这与与轴交点矛盾,故C错.
如图D,解得,无意义,故D错.
②若时,,在定义域内单调递增,当时,,且时,,此时B符合.选项B符合故选B
9. 若函数(且)的图像过第一、三、四象限,则必有( ).
A.B.C.D.
【答案】BC
【解析】若,则的图像必过第二象限,而函数(且)的图像过第一、三、四象限,所以.
当时,要使的图像过第一、三、四象限,则,即.
故选BC
10. 已知函数的图象如图所示,则的图象可能是( )
A.B.
C.D.
【答案】AC
【解析】令,解得、,根据二次函数图形可知,、两个数一个大于,一个大于且小于,①当,时,则在定义域上单调递增,且,即,所以满足条件的函数图形为C;
②当,时,则在定义域上单调递减,且,所以满足条件的函数图形为A;故选AC
(三)指数函数的性质及应用
11.(2022届广东省广州市高三上学期第三次月考)已知,则( )
A.B.
C.D.
【答案】C
【解析】由,得,即,
令,则在上单调递增,所以.故选C.
12. (2022届山东省潍坊市高三上学期期末)已知函数,则下列结论中正确的是( )
A.的定义域为R
B.是奇函数
C.在定义域上是减函数
D.无最小值,无最大值
【答案】BD
【解析】选项A,,解得,故的定义域为,选项A错误;
选项B,函数定义域关于原点对称,且,故是奇函数,选项B正确;
选项C,,故,即在定义域上不是减函数,选项C不正确;
选项D,,令,,由于在上单调递增,在分别单调递减,故函数在分别单调递减,且时,,时,,时,,时,,故函数的值域为,无最小值,无最大值,选项D正确,故选BD
13. (2021届江西省南昌县高三上学期期末)已知,函数的零点分别为,函数的零点分别为,则的最小值为________.
【答案】
【解析】,因为,
所以,.
,又因为,
所以,,
所以,,
所以.令,,则,
所以.
设,,则,在上单调递增,
所以,,故.
三、最新模拟练
14.(2022届北京市西城区高三二模)若函数的定义域和值域的交集为空集,则正数的取值范围是( )
A.B.
C.D.
【答案】B
【解析】因为,所以的定义域为,,
当时,则在上单调递增,所以;
要使定义域和值域的交集为空集,显然,
当时,
若则,此时显然不满足定义域和值域的交集为空集,
若时在上单调递减,此时,
则,
所以,解得,即,故选B
15.(2022届河南省豫西名校高三4月质检)若,则,,的大小关系为( )
A.B.
C.D.
【答案】D
【解析】因为,所以,因为,
所以.故选D.
16.(2022届安徽省合肥市高三下学期第二次教学质量检测)函数(是自然对数的底数)的图象关于( )
A.直线对称B.点对称
C.直线对称D.点对称
【答案】D
【解析】由题意,它与之间没有恒等关系,相加也不为0,AB均错,而,所以的图象关于点对称.故选D.
17.(2022届山西省晋中市高三二模)函数的图象大致是( )
A.B.
C.D.
【答案】B
【解析】由题意可知,对任意的,,
所以,函数的定义域为,
因为,所以函数为偶函数,排除CD选项,
又恒成立,可排除A选项.故选B.
18.(多选)(2022届广东省汕头市高三二模)设a,b,c都是正数,且,则下列结论正确的是( )
A.B.C.D.
【答案】ACD
【解析】设,则,,,
所以
,
即,所以,所以,故D正确;
由,所以,故A正确,B错误;
因为,,
又,所以,即,故C正确;故选ACD
19.(2022届河北省邯郸市大名县高三上学期强化训练)函数的图像恒过一定点,这个定点是___________.
【答案】
【解析】当即时,,故函数过定点.
20.(2022届江苏省南通市高三下学期联考)若,则的最小值为_________.
【答案】
【解析】依题意,,,则,当且仅当,即时取“=”,此时,,
所以,当时,取最小值.
21.(2022届山西省吕梁市名校金科大联考高三上学期12月月考)已知函数(其中e是自然对数的底数).过点的直线与函数的图象交于,两点.
(1)若存在直线,使得,求的取值范围;
(2)证明:.
【解析】 (1)解:由题意可知,直线的斜率存在,设的方程为,
由直线过点,可得,即.
因为直线与函数的图象交于,两点,且,
所以,故.
故若存在直线,使得,的取值范围为.
(2)证明:由题意可知,,整理得,不妨设,
要证,只需证明,
即,
即.
整理得,设,即证,
设,则,
所以在上单调递增,所以,
即,
即,
故.
四、高考真题练
22.(2020全国卷Ⅰ)若,则( )
A.B.C.D.
【答案】B
【解析】设,则为增函数,因为
所以,
所以,所以.
,
当时,,此时,有
当时,,此时,有,所以C、D错误.
故选B.
23. (2020全国卷Ⅱ)若,则( )
A.B.C.D.
【答案】A
【解析】由得:,
令,
为上的增函数,为上的减函数,为上的增函数,
,
,,,则A正确,B错误;
与的大小不确定,故CD无法确定.
故选A.
24.(2019全国卷Ⅲ)设是定义域为的偶函数,且在单调递减,则( )
A.B.
C.D.
【答案】C
【解析】是上的偶函数,.
,又在(0,+∞)单调递减,,
,故选C.
25.(2017全国卷Ⅰ)设为正数,且,则( )
A.B.C.D.
【答案】D
【解析】令,则,,
∴,则
,则,故选D.
26.(2016全国卷Ⅲ)已知,,,则( )
A.B.C.D.
【答案】A
【解析】因为,,故选A.
五、综合提升练
27.(2022届上海市向明中学高三上学期月考)已知函数,设()为实数,且.给出下列结论:
①若,则;
②若,则.
其中正确的是( )
A.①与②均正确B.①正确,②不正确
C.①不正确,②正确D.①与②均不正确
【答案】A
【解析】令函数,
可得函数为单调递增函数,
又由,即,
所以函数为奇函数,图象关于点对称,如图(1)所示,
①中,因为,且,则,
不妨设,
则点,此时直线的方程为,
可得,
则,
可得,
又由,所以,
即,即,所以①正确;
②中,若,不妨设,则,
不妨设,
则点,此时直线的方程为,
可得,
则,
可得,
又由,所以,
即,即,
所以②正确.故选A.
28.(多选)(2022届江苏省盐城 、淮安、 宿迁 、如东等地高三上学期联考)已知函数,,若,则( )
A.
B.
C.
D.
【答案】AC
【解析】对选项A:因为,所以,故选项A正确;
对选项B:因为,所以,故选项B错误;
对选项C:由题意,因为,所以在R上单调递增,
不妨设,则,所以,即,故选项C正确;
对选项D:因为,且,所以由凹凸性有,
又,所以由凹凸性有,
所以有,
即,
即,故选项D错误;故选AC.
29.(2022届陕西省西安市高三上学期练习)设函数和,若两函数在区间上的单调性相同,则把区间叫做的“稳定区间”.已知区间为函数的“稳定区间”,则实数的取值范围是___________
【答案】
【解析】函数在上单调递减,函数在上单调递增,若区间为函数的“稳定区间”,则函数与函数在区间上同增或者同减,
①若两函数在区间上单调递增,
则在区间上恒成立,即,所以;
②若两函数在区间上单调递减,
则在区间上恒成立,即,不等式无解;综上所述:
30.定义在D上的函数,如果满足:对任意,存在常数,都有成立,则称是D上的有界函数,其中称为函数的上界.
已知函数,.
(1)当时,求函数在上的值域,并判断函数在上是否为有界函数,请说明理由;
(2)若函数在上是以3为上界的有界函数,求实数a的取值范围;
(3)若,函数在上的上界是,求的取值范围.
【解析】(1)当时,,显然在上递减,即有,
于是得在上的值域为,显然不存在常数,使成立,
所以函数在上不是有界函数;
(2)依题意,在上恒成立,而,
于是得在上恒成立,
当x≥0时,令,,则,因此,在上递减,
当时,,即当时,取最大值-5,
令,显然在上递增,当时,,即当时,取最小值1,
从而有,
所以实数a的取值范围为;
(3)依题意,,,而,则在上递减,
于是得,即,
①当时,恒有,此时,,
解,当时,,而成立,则,
当时,,解得,
当时,,而不成立,此时无解,
综上得当时,,即当时,,
②当,恒有,此时,,
解得,即当时,,
所以,当时,的取值范围是;当时,的取值范围是.
相关试卷
这是一份高三数学一轮复习五层训练(新高考地区)第8练二次函数与幂函数(原卷版+解析),共21页。试卷主要包含了课本变式练,考点分类练,最新模拟练,高考真题练,综合提升练等内容,欢迎下载使用。
这是一份高三数学一轮复习五层训练(新高考地区)第7练函数的性质(原卷版+解析),共26页。试卷主要包含了课本变式练,考点分类练,最新模拟练,高考真题练,综合提升练等内容,欢迎下载使用。
这是一份高三数学一轮复习五层训练(新高考地区)第5练基本不等式(原卷版+解析),共18页。试卷主要包含了课本变式练,考点分类练,最新模拟练,高考真题练,综合提升练等内容,欢迎下载使用。









