

所属成套资源:高三数学一轮复习五层训练(新高考地区)(原卷版+解析)
高三数学一轮复习五层训练(新高考地区)第19练y=Asin(ωx+φ)及三角函数的应用(原卷版+解析)
展开
这是一份高三数学一轮复习五层训练(新高考地区)第19练y=Asin(ωx+φ)及三角函数的应用(原卷版+解析),共32页。试卷主要包含了课本变式练,考点分类练,最新模拟练,高考真题练,综合提升练等内容,欢迎下载使用。
1.(人A必修一P239练习T2变式)将函数图象上的所有点向左平移个单位长度,则所得图象的函数解析式是( )
A.B.
C.D.
2.(人A必修一P240习题5.6T6变式)某时钟的秒针端点到中心点的距离为5cm,秒针绕点匀速旋转,当时间:时,点与钟面上标12的点重合,当两点间的距离为(单位:cm),则等于( )
A.B.C.D.
3. (人A必修一P240习题5.6T7变式)水车是我国劳动人民创造发明的一种灌溉工具,作为中国农耕文化的组成部分,充分体现了中华民族的创造力,见证了中国农业文明.水车的外形酷似车轮,在轮的边缘装有若干个水斗,借助水势的运动惯性冲动水车缓缓旋转,将水斗内的水逐级提升.某水车轮的半径为5米,圆心距水面的高度为4米,水车按逆时针方向匀速转动,每分钟转动2圈,当其中的一个水斗到达最高点时开始计时,设水车转动(分钟)时水斗距离水面的高度(水面以上为正,水面以下为负)为(米),下列选项正确的是( )
A.()
B.()
C.是函数的周期
D.在旋转一周的过程中,水斗距离水面高度不低于6.5米的时间为10秒.
4. (人A必修一P240习题5.6T3变式)若函数的图象向左平移个单位得到函数的图象,则________.
二、考点分类练
(一) 的图象变换
5.(2022届四川省宜宾市高三三诊)要得到函数的图像,只需把函数的图像( )
A.向右平移个单位B.向左平移个单位C.向右平移个单位D.向左平移个单位
6.(2022届四川省凉山州高三第三次诊断)将函数的图象向左平移个单位,再将纵坐标伸长为原来的4倍(横坐标不变)得到函数的图象,且的图象上一条对称轴与一个对称中心的最小距离为,对于函数有以下几个结论:
(1);
(2)它的图象关于直线对称;
(3)它的图象关于点对称;
(4)若,则;
则上述结论正确的个数为( )
A.1B.2C.3D.4
7.(2022届江苏省南通市如皋市高三5月适应性考试)已知函数,先将的图象上所有点的纵坐标不变,横坐标变为原来的倍,再将图象向右平移个单位长度,得到函数的图象,则( )
A.B.的图象关于对称
C.的最小正周期为D.在上单调递减
8.(2022届辽宁省大连市高三第二次模拟)将函数的图像分别向左、向右各平移个单位长度后,所得的两个函数图像的对称轴重合,则的最小值为___________.
(二) 的图象及应用
9.(2022届四川省射洪市高三下学期模拟)已知函数 的部分图象如图所示,将函数 的图象上所有点的横坐标变为原来的,纵坐标不变,再将所得函数图象向右平移个单位长度,得到函数 的图象,则下列关于函数的说法正确的是( )
A.的最小正周期为
B.在区间上单调递增
C.的图象关于直线x=对称
D.的图象关于点中心对称
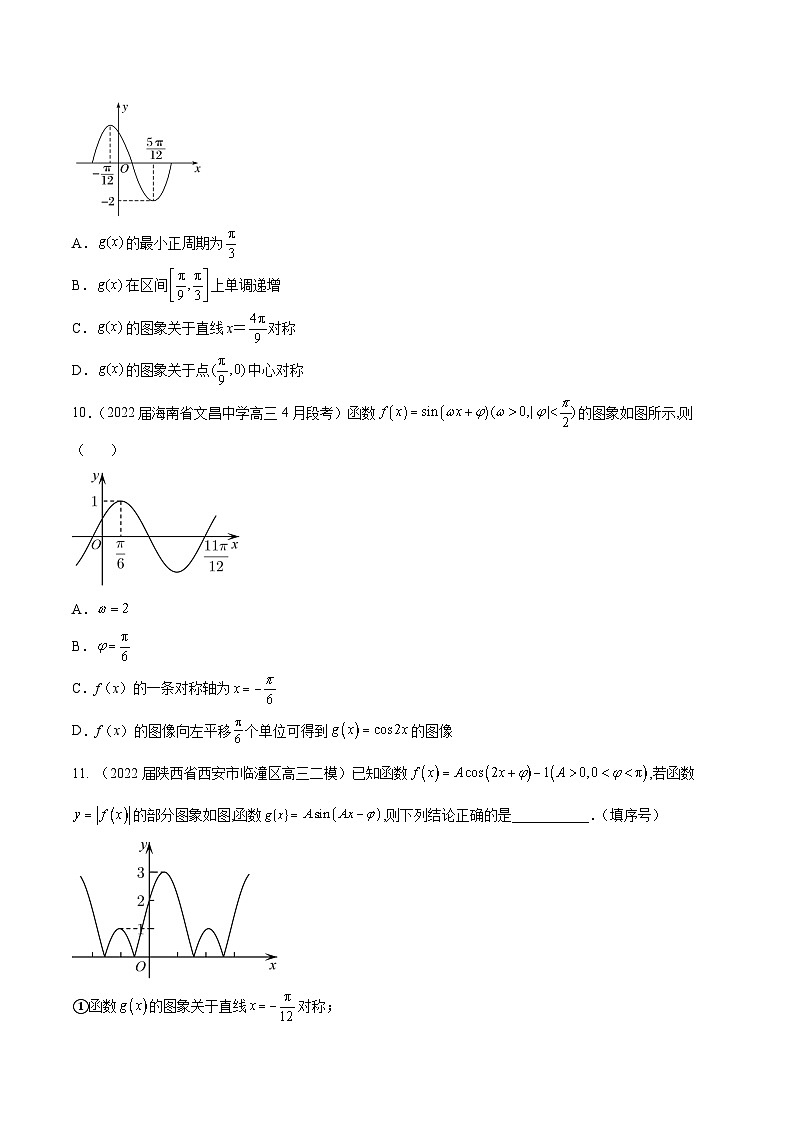
10.(2022届海南省文昌中学高三4月段考)函数的图象如图所示,则( )
A.
B.
C.f(x)的一条对称轴为
D.f(x)的图像向左平移个单位可得到的图像
11. (2022届陕西省西安市临潼区高三二模)已知函数,若函数的部分图象如图,函数,则下列结论正确的是___________.(填序号)
①函数的图象关于直线对称;
②函数的图象关于点对称;
③将函数的图象向左平移个单位长度可得到函数的图象;
④函数在区间上的单调递减区间为.
(三)三角函数的应用
12. 某艺术展览馆在开馆时间段(9:00—16:00)的参观人数(单位:千)随时间(单位:时)的变化近似满足函数关系,且下午两点整参观人数为7千,则开馆中参观人数的最大值为( )
A.1万B.9千C.8千D.7千
13. (2022届湖北省高三下学期5月联考)阻尼器是一种以提供运动的阻力,从而达到减振效果的专业工程装置.由物理学知识可知,某阻尼器模型的运动过程可近似为单摆运动,其离开平衡位置的位移和时间的函数关系式为,其中,若该阻尼器模型在摆动过程中位移为1的相邻时刻差为,则的可能取值为( )
A.2B.3C.4D.6
14.如图所示,在平面直角坐标系中,动点以每秒的角速度从点出发,沿半径为2的上半圆逆时针移动到,再以每秒的角速度从点沿半径为1的下半圆逆时针移动到坐标原点,则上述过程中动点的纵坐标关于时间的函数表达式为___________.
三、最新模拟练
15.(2022届重庆市第一中学校高三5月月考)几何学中把变换前后两点间距离保持不变的变换称为刚体变换.在平面中作图形变换,易知平移变换是一种刚体变换.以下两个函数与,其中不能由通过平移刚体变换得到的是( )
A.,B.,
C.,D.,
16. (2022届广东省惠州市六校联盟高三联考)已知函数的部分图像如图所示,则将的图像向左平移个单位后,所得图像的函数解析式为( )
A.B.
C.D.
17.(2022届重庆市高三下学期第七次质量检测) “传得淮南术最佳,皮肤退尽见精华.旋转磨上流琼液,煮月铛中滚雪花.”推豆花是传统的劳动技能,早在汉朝劳动人民发明了豆腐,通过连杆带动石磨转动,碾碎黄豆,磨出豆浆,再利用胆水,点出豆花,压成豆腐(如图1).推豆磨的过程(图2),推磨人(身体在点)发力推动连杆,带动石磨逆时针转动,随着连杆移动,人随着连杆移动适当倾斜.当连杆在处与磨盘圆面相切时,人侧倾到,此时能使得推磨效率最大.若,,,,则下列等式成立的是( )
A.B.
C.D.
18. (多选)(2022届湖北省重点高中智学联盟2高三联考)水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为的水车,一个水斗从点出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时6秒.经过秒后,水斗旋转到点,设点的坐标为,其纵坐标满足,则下列结论正确的是( )
A.
B.当时,函数单调递增
C.当时,点的纵坐标越来越小
D.当时,
19.(多选)(2022届重庆市第十一中学高三月考) 已知,具有下面三个性质:①将的图象右移个单位得到的图象与原图象重合;②,;③在时存在两个零点,给出下列判断,其中正确的是( )
A.在时单调递减
B.
C.将的图象左移个单位长度后得到的图象关于原点对称
D.若与图象关于对称,则当时,的值域为
20.(2022届陕西省西安市周至县高三三模) 若函数的图像向右平移个单位长度后与函数的图象重合,则的一个可能的值为___________;
21. (2022届山东省潍坊市高三三模)已知函数向右平移个单位长度后得到.若对于任意的,总存在,使得,则的最小值为______.
22. (2022届江苏省扬州市高三月考)函数(其中)的部分图象如图所示,把函数的图像向右平移个单位长度,再向下平移个单位,得到函数的图像.
(1)当时,若方程恰好有两个不同的根,求的取值范围及的值;
(2)令,若对任意都有恒成立,求的最大值.
四、高考真题练
23.(2021全国卷Ⅰ)把函数图像上所有点的横坐标缩短到原来的倍,纵坐标不变,
再把所得曲线向右平移个单位长度,得到函数的图像,则( )
A.B.C.D.
24.(2020全国卷Ⅰ)设函数在的图像大致如下图,则f(x)的最小正周期为( )
( )
A.B.C.D.
25.(2017全国卷Ⅰ)已知曲线,,则下面结论正确的是( )
A.把上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线
B.把上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线
C.把上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线
D.把上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线
26.(2016全国卷Ⅱ)若将函数的图像向左平移个单位长度,则平移后图象的对称轴为( )
A.B.
C.D.
五、综合提升练
27.关于函数y=sin(2x+φ)()有如下四个命题:
甲:该函数在上单调递增;
乙:该函数图象向右平移个单位长度得到一个奇函数;
丙:该函数图象的一条对称轴方程为;
丁:该函数图像的一个对称中心为.
如果只有一个假命题,则该命题是( )
A.甲B.乙C.丙D.丁
28.已知函数且对于 都有成立.现将函数 的图象向右平移个单位长度,再把所有点的横坐标伸长到原来的2倍(纵坐标不变)得到函数的图象,则下列说法正确的是( )
A.函数B.函数相邻的对称轴距离为
C.函数是偶函数D.函数在区间上单调递增
29.(2022届重庆市第八中学校高三下学期高考适应性月考)某城市要在广场中央的圆形地面设计一块浮雕,以彰显城市积极向上的活力,某公司设计方案如图,等腰△PMN的顶点P在半径为20m的大O上,点M,N在半径为10m的小O上,点O,点P在弦MN的同侧.则当△POM与△MON面积之和最大时∠MON=___________.
30.已知函数,.
(1)若图象纵坐标不变,横坐标变为原来的2倍,再向右平移个单位,得到的图象在上单调递增,求的最大值;
(2)若函数在内恰有3个零点,求的取值范围.
第19练 及三角函数的应用
一、课本变式练
1.(人A必修一P239练习T2变式)将函数图象上的所有点向左平移个单位长度,则所得图象的函数解析式是( )
A.B.
C.D.
【答案】A
【解析】将函数图象上的所有点向左平移个单位长度,则所得图象的函数解析式是.故选A
2.(人A必修一P240习题5.6T6变式)某时钟的秒针端点到中心点的距离为5cm,秒针绕点匀速旋转,当时间:时,点与钟面上标12的点重合,当两点间的距离为(单位:cm),则等于( )
A.B.C.D.
【答案】D
【解析】由题知,圆心角为,过O作AB的垂线,则.故选D
3. (人A必修一P240习题5.6T7变式)水车是我国劳动人民创造发明的一种灌溉工具,作为中国农耕文化的组成部分,充分体现了中华民族的创造力,见证了中国农业文明.水车的外形酷似车轮,在轮的边缘装有若干个水斗,借助水势的运动惯性冲动水车缓缓旋转,将水斗内的水逐级提升.某水车轮的半径为5米,圆心距水面的高度为4米,水车按逆时针方向匀速转动,每分钟转动2圈,当其中的一个水斗到达最高点时开始计时,设水车转动(分钟)时水斗距离水面的高度(水面以上为正,水面以下为负)为(米),下列选项正确的是( )
A.()
B.()
C.是函数的周期
D.在旋转一周的过程中,水斗距离水面高度不低于6.5米的时间为10秒.
【答案】AD
【解析】由题意得,如图,轴,,点经过分钟后到达点,则为点到水面的距离,且,因为每分钟转2圈,所以,得角速度,故,又,所以,所以,即.故A正确,B错误;又因为函数的周期,Z,由周期的定义结合函数的定义域可得C错误;令,得,解得或,Z,
当时,或,即旋转一周的过程中(30s),有25-5=20s,水斗A距离水面高度低于6.5米,所以有30-20=10s的时间不低于6.5米,故D正确.故选AD.
4. (人A必修一P240习题5.6T3变式)若函数的图象向左平移个单位得到函数的图象,则________.
【答案】
【解析】函数,则.
二、考点分类练
(一) 的图象变换
5.(2022届四川省宜宾市高三三诊)要得到函数的图像,只需把函数的图像( )
A.向右平移个单位B.向左平移个单位C.向右平移个单位D.向左平移个单位
【答案】C
【解析】把函数的图象向右平移个单位得到
把函数的图象向左平移个单位得到
把函数的图象向右平移个单位得到,
把函数的图象向左平移个单位得到,
故C正确;故选C
6.(2022届四川省凉山州高三第三次诊断)将函数的图象向左平移个单位,再将纵坐标伸长为原来的4倍(横坐标不变)得到函数的图象,且的图象上一条对称轴与一个对称中心的最小距离为,对于函数有以下几个结论:
(1);
(2)它的图象关于直线对称;
(3)它的图象关于点对称;
(4)若,则;
则上述结论正确的个数为( )
A.1B.2C.3D.4
【答案】C
【解析】由题意得:,向左平移个单位,再将纵坐标伸长为原来的4倍(横坐标不变)得到函数.
对于选项A:由的图象上一条对称轴与一个对称中心的最小距离为,最小正周期,即
,解得,故,所以(1)错误;
当时,代入可知,故图像的一条对称轴是,故(2)正确;
当时,代入可知,故图像的一个对称点是,故(3)正确;
若,则,所以
因此在上的取值范围是,故(4)正确;
由上可知(2)(3)(4)正确,正确的个数为个.故选C
7.(2022届江苏省南通市如皋市高三5月适应性考试)已知函数,先将的图象上所有点的纵坐标不变,横坐标变为原来的倍,再将图象向右平移个单位长度,得到函数的图象,则( )
A.B.的图象关于对称
C.的最小正周期为D.在上单调递减
【答案】BCD
【解析】对于A选项,将的图象上所有点的纵坐标不变,横坐标变为原来的倍,可得到函数的图象,再将所得图象向右平移个单位长度,可得到函的图象,A错;对于B选项,,B对;对于C选项,函数的最小正周期为,C对;对于D选项,当时,,所以,函数在区间上单调递减D对.故选BCD.
8.(2022届辽宁省大连市高三第二次模拟)将函数的图像分别向左、向右各平移个单位长度后,所得的两个函数图像的对称轴重合,则的最小值为___________.
【答案】3
【解析】将函数的图象分别向左、向右各平移个单位长度后,得到,,因为两个函数图象的对称轴重合,所以,Z,所以,Z,因为,所以当时,取得最小值为3.
(二) 的图象及应用
9.(2022届四川省射洪市高三下学期模拟)已知函数 的部分图象如图所示,将函数 的图象上所有点的横坐标变为原来的,纵坐标不变,再将所得函数图象向右平移个单位长度,得到函数 的图象,则下列关于函数的说法正确的是( )
A.的最小正周期为
B.在区间上单调递增
C.的图象关于直线x=对称
D.的图象关于点中心对称
【答案】C
【解析】由函数图象知,,所以,所以 ,
因为函数图象过点,所以,则,解得,又,所以,所以,将函数的图象上所有点的横坐标变为原来的,得到,纵坐标不变,再将所得函数图象向右平移个单位长度,得到,的最小正周期,故A错误;当时,,此时单调递减,故B错误;
令,则,当时,,故C正确;因为,故D错误.故选C.
10.(2022届海南省文昌中学高三4月段考)函数的图象如图所示,则( )
A.
B.
C.f(x)的一条对称轴为
D.f(x)的图像向左平移个单位可得到的图像
【答案】ABD
【解析】由题图可得,解得,A正确.∴,把(,1)代入得,∵,∴,B正确.,不是整数,C错
f(x)的图像向左平移个单位可得,D正确
故选ABD
11. (2022届陕西省西安市临潼区高三二模)已知函数,若函数的部分图象如图,函数,则下列结论正确的是___________.(填序号)
①函数的图象关于直线对称;
②函数的图象关于点对称;
③将函数的图象向左平移个单位长度可得到函数的图象;
④函数在区间上的单调递减区间为.
【答案】③
【解析】由函数的部分图象知的最大值是1,最小值是-3,或最大值是3,最小值是-1,不论哪种情形都有,,若,则,,无解,
若,则,,又,所以,,
时,,①错;时,,②错;
的图象向左平移个单位长度可得到
的图象,③正确;
时,,,先减后增,④错.故答案为③.
(三)三角函数的应用
12. 某艺术展览馆在开馆时间段(9:00—16:00)的参观人数(单位:千)随时间(单位:时)的变化近似满足函数关系,且下午两点整参观人数为7千,则开馆中参观人数的最大值为( )
A.1万B.9千C.8千D.7千
【答案】B
【解析】下午两点整即,当时,.即,∴,∵当时,,∴当时,取得最大值,且最大值为.故选B
13. (2022届湖北省高三下学期5月联考)阻尼器是一种以提供运动的阻力,从而达到减振效果的专业工程装置.由物理学知识可知,某阻尼器模型的运动过程可近似为单摆运动,其离开平衡位置的位移和时间的函数关系式为,其中,若该阻尼器模型在摆动过程中位移为1的相邻时刻差为,则的可能取值为( )
A.2B.3C.4D.6
【答案】AC
【解析】令得或,,所以两相邻时刻差为或,
当时,得,当时,得.故选AC.
14.如图所示,在平面直角坐标系中,动点以每秒的角速度从点出发,沿半径为2的上半圆逆时针移动到,再以每秒的角速度从点沿半径为1的下半圆逆时针移动到坐标原点,则上述过程中动点的纵坐标关于时间的函数表达式为___________.
【答案】
【解析】由三角函数的定义可得:当动点在半径为2的上半圆上运动时,,终边对应的角度为,所以点坐标为,当动点在半径为1的下半圆上运动时,,终边对应的角度为,所以点坐标为,
综上:动点的纵坐标关于时间的函数表达式为
三、最新模拟练
15.(2022届重庆市第一中学校高三5月月考)几何学中把变换前后两点间距离保持不变的变换称为刚体变换.在平面中作图形变换,易知平移变换是一种刚体变换.以下两个函数与,其中不能由通过平移刚体变换得到的是( )
A.,B.,
C.,D.,
【答案】D
【解析】向左平移个单位即可得到;因为,所以先向左平移1个单位,再向下平移1个单位即可得到;向上平移1个单位,即可得到;因为,故不能通过上下左右平移得到.
故选D
16. (2022届广东省惠州市六校联盟高三联考)已知函数的部分图像如图所示,则将的图像向左平移个单位后,所得图像的函数解析式为( )
A.B.
C.D.
【答案】B
【解析】由题,,由图,,
,所以,向左平移个单位后,
得到,故选B.
17.(2022届重庆市高三下学期第七次质量检测) “传得淮南术最佳,皮肤退尽见精华.旋转磨上流琼液,煮月铛中滚雪花.”推豆花是传统的劳动技能,早在汉朝劳动人民发明了豆腐,通过连杆带动石磨转动,碾碎黄豆,磨出豆浆,再利用胆水,点出豆花,压成豆腐(如图1).推豆磨的过程(图2),推磨人(身体在点)发力推动连杆,带动石磨逆时针转动,随着连杆移动,人随着连杆移动适当倾斜.当连杆在处与磨盘圆面相切时,人侧倾到,此时能使得推磨效率最大.若,,,,则下列等式成立的是( )
A.B.
C.D.
【答案】C
【解析】由题意知,,延长交于点E,则,有,
如图,
,
在中,,即,所以,
在中,,即,所以,
即.故选C.
18. (多选)(2022届湖北省重点高中智学联盟2高三联考)水车在古代是进行灌溉引水的工具,是人类的一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个半径为的水车,一个水斗从点出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时6秒.经过秒后,水斗旋转到点,设点的坐标为,其纵坐标满足,则下列结论正确的是( )
A.
B.当时,函数单调递增
C.当时,点的纵坐标越来越小
D.当时,
【答案】CD
【解析】因为,所以,因为旋转一周用时6秒,所以角速度,
所以,所以根据三角函数的定义可得,
所以,所以A错误,对于B,当时,,则函数在此区间上不单调,所以B错误,对于C,当时,,所以函数在上单调递减,所以点的纵坐标越来越小,所以C正确,对于D,当时, ,所以,因为,所以,所以D正确,故选CD
19.(多选)(2022届重庆市第十一中学高三月考) 已知,具有下面三个性质:①将的图象右移个单位得到的图象与原图象重合;②,;③在时存在两个零点,给出下列判断,其中正确的是( )
A.在时单调递减
B.
C.将的图象左移个单位长度后得到的图象关于原点对称
D.若与图象关于对称,则当时,的值域为
【答案】BCD
【解析】,将右移个单位得到的函数解析式为,又该函数的图象与原图象重合,所以,
所以,又在时存在两个零点,所以,所以,即,所以,所以,所以,又,,所以,所以,所以,又,所以,所以,由得,
所以函数的单调递减区间为当时,函数在上单调递减;
由得,所以函数的单调递增区间为,当时,函数在上单调递增;
所以函数在上单调递减,在上单调递增,故A错误;
,
,
,
所以,故B正确;
将的图象左移个单位长度后得到的图象的解析式为,
又,所以函数为奇函数,
所以的图象关于原点对称,故C正确;
关于对称的区间为,
当时,,所以,
所以当时,的值域为,故D正确.故选BCD
20.(2022届陕西省西安市周至县高三三模) 若函数的图像向右平移个单位长度后与函数的图象重合,则的一个可能的值为___________;
【答案】(答案不唯一)
【解析】将函数的图像向右平移个单位长度后,得到函数的图像,
即与函数的图像重合,即,,
所以,,故答案为(答案不唯一).
21. (2022届山东省潍坊市高三三模)已知函数向右平移个单位长度后得到.若对于任意的,总存在,使得,则的最小值为______.
【答案】
【解析】函数向右平移个单位长度后得到,因为,所以,所以,因为对于任意的,总存在,使得,所以的取值范围应包含,根据余弦函数的性质,为使取最小值,只需函数在上单调且值域为即可.由可得,因此的最小值为.故答案为.
22. (2022届江苏省扬州市高三月考)函数(其中)的部分图象如图所示,把函数的图像向右平移个单位长度,再向下平移个单位,得到函数的图像.
(1)当时,若方程恰好有两个不同的根,求的取值范围及的值;
(2)令,若对任意都有恒成立,求的最大值.
【解析】(1)根据图像可知
,
代入得,,,
把函数的图像向右平移个单位长度,再向下平移个单位,得到函数
在单调递增,在单调递减,在单调递增,
且,
,
方程恰好有两个不同的根,
的取值范围
令
对称轴为,
或
时,;时,.
(2)由(1)可知
,对任意都有恒成立
令,即在上恒成立,
是关于的二次函数,开口向上,则恒成立
而的最大值,在或时取到最大值
则,解得
所以,则的最大值为.
四、高考真题练
23.(2021全国卷Ⅰ)把函数图像上所有点的横坐标缩短到原来的倍,纵坐标不变,
再把所得曲线向右平移个单位长度,得到函数的图像,则( )
A.B.C.D.
【答案】B
【解析】把函数图像上所有点的横坐标缩短到原来的倍,纵坐标不变,再把所得曲线向右平移个单位长度,得到函数的图像,把函数的图像,向左平移个单位长度,
得到的图像;再把图像上所有点的横坐标变为原来的2倍,纵坐标不变,
可得的图像.故选.
24.(2020全国卷Ⅰ)设函数在的图像大致如下图,则f(x)的最小正周期为( )
( )
A.B.C.D.
【答案】C
【解析】由图可得:函数图象过点,将它代入函数可得:
又是函数图象与轴负半轴的第一个交点,所以,解得:
所以函数的最小正周期为,故选C
25.(2017全国卷Ⅰ)已知曲线,,则下面结论正确的是( )
A.把上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线
B.把上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线
C.把上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线
D.把上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线
【答案】D
【解析】因为函数名不同,所以先将利用诱导公式转化成与相同的函数名,则,则由上各点的横坐标缩短到原来的倍变为,再将曲线向左平移个单位得到,故选D.
26.(2016全国卷Ⅱ)若将函数的图像向左平移个单位长度,则平移后图象的对称轴为( )
A.B.
C.D.
【答案】B
【解析】将函数的图像向左平移个单位长度的到 的图像,令 则,故选B.
五、综合提升练
27.关于函数y=sin(2x+φ)()有如下四个命题:
甲:该函数在上单调递增;
乙:该函数图象向右平移个单位长度得到一个奇函数;
丙:该函数图象的一条对称轴方程为;
丁:该函数图像的一个对称中心为.
如果只有一个假命题,则该命题是( )
A.甲B.乙C.丙D.丁
【答案】D
【解析】令,则函数的增区间为…①;
函数图象向右平移个单位长度得到…②;
令…③;令…④.
若甲错误,则乙丙丁正确,由②,由函数的奇偶性性,令,由①,函数的增区间为,则甲正确,矛盾.令,由①,函数的增区间为,则甲错误,满足题意.由③,函数的对称轴方程为,时,,则丙正确.由④,函数的对称中心为,令,丁错误.不合题意;
若乙错误,则甲丙丁正确,易知函数增区间的的两个端点的中点为对称中心,由①,令,结合④,令,由函数的奇偶性,取k=0,,由③,,令,则丙错误.不合题意;
若丙错误,则甲乙丁正确,由②,由函数的奇偶性,令,由①,函数的增区间为,则甲错误,不合题意.令,由①,函数的增区间为,甲正确.取区间中点,则丁错误.不合题意;
若丁错误,则甲乙丙正确. 由②,由函数的奇偶性,令,由①,函数的增区间为,则甲错误,不合题意.令,,由①,函数的增区间为,甲正确.由③,.k=-2时,,则丙正确.由④,,令,④错误.满足题意.综上:该命题是丁.故选D.
28.已知函数且对于 都有成立.现将函数 的图象向右平移个单位长度,再把所有点的横坐标伸长到原来的2倍(纵坐标不变)得到函数的图象,则下列说法正确的是( )
A.函数B.函数相邻的对称轴距离为
C.函数是偶函数D.函数在区间上单调递增
【答案】ABCD
【解析】因为对于都有成立,所以, ,
所以对于 都成立,可得的周期,所以,
所以,将函数的图象向右平移 个单位长度,可得
再把所有点的横坐标伸长到原来的2倍可得 ,
对于选项A: ,
故选项A正确;对于选项B:函数周期为,所以相邻的对称轴距离为 ,故选项B正确;对于选项C:是偶函数,故选项C正确;
对于选项D:当,,所以函数 在区间上单调递增,故选项D正确,
故选ABCD
29.(2022届重庆市第八中学校高三下学期高考适应性月考)某城市要在广场中央的圆形地面设计一块浮雕,以彰显城市积极向上的活力,某公司设计方案如图,等腰△PMN的顶点P在半径为20m的大O上,点M,N在半径为10m的小O上,点O,点P在弦MN的同侧.则当△POM与△MON面积之和最大时∠MON=___________.
【答案】
【解析】令,延长交于,则,(),
所以△POM与△MON面积之和为
,
所以
令,得(舍去)或,得
当时,,函数单调递增,
当时,,函数单调递减,
所以当时,取得最大值,此时
30.已知函数,.
(1)若图象纵坐标不变,横坐标变为原来的2倍,再向右平移个单位,得到的图象在上单调递增,求的最大值;
(2)若函数在内恰有3个零点,求的取值范围.
【解析】 (1) 图象纵坐标不变,横坐标变为原来的2倍,再向右平移个单位得到函数,
因为,所以,
因为,所以,
又因为得到的图象在上单调递增,所以,解,
所以的最大值为.
(2) ,
令,
因为,所以,,
所以,,
令,显然不是其方程的解,所以得,,
画出函数和函数的图象,如下图,
则当时,对应的,而当时,对应的只有一个解,不满足题意;
当时,此时没有的值对应,所以此时无解,不满足题意;
当时,对应的,而当时,对应的有两个解,不满足题意;
当时,对应的,,而此时对应的只有两个解,不满足题意;
当时,令,得或 ,此时对应的,,而当对应的时,对应一个的值,而当时对应两个的值,所以此时有三个解,满足题意;
当时,对应的,而此时对应的只有一个解,不满足题意;
故的取值范围为.
相关试卷
这是一份高考数学一轮复习题型讲解+专题训练(新高考专用)专题24函数y=Asin(ωx+φ)的图象(原卷版+解析),共48页。试卷主要包含了(2023·全国甲等内容,欢迎下载使用。
这是一份高考数学一轮复习考点微专题(新高考地区专用)考向20函数y=Asin(ωx+φ)的图象及其应用(重点)(原卷版+解析),共56页。
这是一份高考数学一轮复习小题多维练(新高考专用)第14练函数y=Asin(ωx+ϕ)及三角函数的应用(原卷版+解析),共21页。









